Skip to main content

Advertisement

Springer Nature Link
Log in

Dynamic phenomena of a financial hyperchaotic system and DNA sequences for image encryption

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

With advances in modern technology, the security of information, including the protection of digital images, is of particular interest. Due to the type of special storage format of images and the fateful dimension of 1D map that have a small secret key space, in this paper, a joint-based encryption technique on the pseudo-random and sophisticated character of hyperchaotic behavior and DNA coding is proposed. The entire dynamics of a financial hyperchaotic system is studied for a better selection of the sequence key using nonlinear analysis tools. A rich dynamic of this analysis reveals a plethora of phenomena such as multistability and offset boosting, which, to our knowledge, have not yet been the subject of a study on financial hyperchaotic systems. The set consisting of the pseudo-random aspect of the financial hyperchaotic system used in all stages of encryption, DNA coding (algebraic operations, complementation, and DNA rules), and the scrambling of the positions of each image pixel is exploited to reinforce the effectiveness of the confusion and diffusion of digital images. To analyze the security and robustness of the proposed algorithm, some security tests such as histogram analysis, correlation, information entropy, as well as key analysis are carried out. The values of correlation coefficients of the encrypted images using the proposed scheme are close to zero, The entropy values of the test images are overall greater than 7.99 and the key space of the is greater than 2100. Besides, differential analysis shows that the number of pixel change rate (NPCR) and unified average change intensity (UACI) for the proposed technique are greater than 99.50% and 30%, respectively. Furthermore, the quantitative analyses of occlusion and data loss attacks as well as the results of comparison with some advanced algorithms show the efficiency and security of the proposed cryptosystem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.
Fig. 11.
Fig. 12.
Fig. 13.

Similar content being viewed by others

References

  1. Adleman LM (1994) Molecular computation of solutions to combinatorial problems. Science 266(5187):1021–1024

    Google Scholar 

  2. Amani HR, Yaghoobi M (2019) A new approach in adaptive encryption algorithm for color images based on DNA sequence operation and hyper-chaotic system. Multimed Tools Appl 78(15):21537–21556

    Google Scholar 

  3. Argyris JH, Faust G, Haase M, Friedrich R (2015) An exploration of dynamical systems and chaos: completely revised and enlarged second edition. Springer

  4. Babaei M (2013) A novel text and image encryption method based on chaos theory and DNA computing. Nat Comput 12(1):101–107

    MathSciNet  MATH  Google Scholar 

  5. Behnia S, Akhshani A, Mahmodi H, Akhavan A (2008) A novel algorithm for image encryption based on mixture of chaotic maps. Chaos, Solitons & Fract 35(2):408–419. https://doi.org/10.1016/j.chaos.2006.05.011

  6. Biham E, Shamir A, (1992) Differential cryptanalysis of the full 16-round DES. In: Annual International Cryptology Conference. Springer, pp 487–496

  7. Chai X, Chen Y, Broyde L (2017) A novel chaos-based image encryption algorithm using DNA sequence operations. Opt Lasers Eng 88:197–213

    Google Scholar 

  8. Chai X, Gan Z, Yuan K, Chen Y, Liu X (2019) A novel image encryption scheme based on DNA sequence operations and chaotic systems. Neural Comput & Applic 31(1):219–237

    Google Scholar 

  9. Chai X, Fu X, Gan Z, Lu Y, Chen Y (2019) A color image cryptosystem based on dynamic DNA encryption and chaos. Signal Process 155:44–62

    Google Scholar 

  10. Chen J, Zhu Z-l, L-b Z, Zhang Y, Yang B-q (2018) Exploiting self-adaptive permutation–diffusion and DNA random encoding for secure and efficient image encryption. Signal Process 142:340–353

    Google Scholar 

  11. Cui S, Peng W, Song C (2019) Research on DNA Cryptosystem Based on DNA Computing. In: International conference on bio-inspired computing: theories and applications. Springer, Singapore, pp 189–197

  12. Dagadu JC, Li J, Aboagye EO, Deynu FK (2019) Medical image encryption scheme based on multiple Chaos and DNA coding. IJ Network Security 21(1):83–90

    Google Scholar 

  13. Enayatifar R, Abdullah AH, Isnin IF (2014) Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence. Opt Lasers Eng 56:83–93. https://doi.org/10.1016/j.optlaseng.2013.12.003

  14. Faragallah OS (2015) Efficient confusion–diffusion chaotic image cryptosystem using enhanced standard map. Signal, Image Video Process 9(8):1917–1926. https://doi.org/10.1007/s11760-014-0683-y

  15. Folifack Signing V, Kengne J (2019) Reversal of period-doubling and extreme multistability in a novel 4D chaotic system with hyperbolic cosine nonlinearity. Int J Dynamics Control 7(2):439–451. https://doi.org/10.1007/s40435-018-0452-9

    Article  MathSciNet  Google Scholar 

  16. Gehani A, LaBean T, Reif J (2000) DNA-based cryptography. DIMACS DNA based computers V. American Mathematical Society

  17. Gong L, Qiu K, Deng C, Zhou N (2019) An optical image compression and encryption scheme based on compressive sensing and RSA algorithm. Opt Lasers Eng 121:169–180

    Google Scholar 

  18. Guan Z, Si G, Wu J, Zhu L, Zhang Z, Ma Y (2017) Utility-privacy tradeoff based on random data obfuscation in internet of energy. IEEE Access 5:3250–3262

    Google Scholar 

  19. Guesmi R, Farah MAB, Kachouri A, Samet M (2016) A novel chaos-based image encryption using DNA sequence operation and secure hash algorithm SHA-2. Nonlinear Dynamics 83(3):1123–1136

    MathSciNet  MATH  Google Scholar 

  20. Hu T, Liu Y, Gong L-H, Guo S-F, Yuan H-M (2017) Chaotic image cryptosystem using DNA deletion and DNA insertion. Signal Process 134:234–243

    Google Scholar 

  21. Hu T, Liu Y, Gong L-H, Ouyang C-J (2017) An image encryption scheme combining chaos with cycle operation for DNA sequences. Nonlinear Dynamics 87(1):51–66

    Google Scholar 

  22. Huang X, Ye G (2014) An image encryption algorithm based on hyper-chaos and DNA sequence. Multimed Tools Appl 72(1):57–70

    Google Scholar 

  23. Huang Z-J, Cheng S, Gong L-H, Zhou N-R (2020) Nonlinear optical multi-image encryption scheme with two-dimensional linear canonical transform. Opt Lasers Eng 124:105821

    Google Scholar 

  24. Jahanshahi H, Yousefpour A, Wei Z, Alcaraz R, Bekiros S (2019) A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization. Chaos, Solitons Fract 126:66–77. https://doi.org/10.1016/j.chaos.2019.05.023

  25. Jain A, Rajpal N (2016) A robust image encryption algorithm resistant to attacks using DNA and chaotic logistic maps. Multimed Tools Appl 75(10):5455–5472. https://doi.org/10.1007/s11042-015-2515-7

  26. Jian J, Deng X, Wang J (2009) Globally exponentially attractive set and synchronization of a class of chaotic finance system. In: International Symposium on Neural Networks. Springer, pp 253–261

  27. Kengne J (2017) On the dynamics of Chua’s oscillator with a smooth cubic nonlinearity: occurrence of multiple attractors. Nonlinear Dynamics 87(1):363–375

    MathSciNet  Google Scholar 

  28. Kengne J, Mogue RLT (2019) Dynamic analysis of a novel jerk system with composite tanh-cubic nonlinearity: chaos, multi-scroll, and multiple coexisting attractors. Int J Dynamics Control 7(1):112–133

    Google Scholar 

  29. Kengne J, Tsafack N, Kengne LK (2018) Dynamical analysis of a novel single Opamp-based autonomous LC oscillator: antimonotonicity, chaos, and multiple attractors. Int J Dynamics Control 6(4):1543–1557

    MathSciNet  Google Scholar 

  30. Kengne J, Abdolmohammadi H, Signing VF, Jafari S, Kom G Chaos and Coexisting Bifurcations in a Novel 3D Autonomous System with a Non-Hyperbolic Fixed Point: Theoretical Analysis and Electronic Circuit Implementation.

  31. King OD, Gaborit P (2007) Binary templates for comma-free DNA codes. Discret Appl Math 155(6–7):831–839

    MathSciNet  MATH  Google Scholar 

  32. Kocarev L, Tasev Z (2003) Public-key encryption based on Chebyshev maps. In: Proceedings of the 2003 International Symposium on Circuits and Systems, 2003. ISCAS'03. IEEE, pp III-III

  33. Li Y, Wang C, Chen H (2017) A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt Lasers Eng 90:238–246

    Google Scholar 

  34. Li B, Liao X, Jiang Y (2018) A novel image encryption scheme based on logistic map and dynatomic modular curve. Multimed Tools Appl 77(7):8911–8938

    Google Scholar 

  35. Lian S (2008) Multimedia content encryption: techniques and applications. CRC press

  36. Liao X, Kulsoom A, Ullah S (2016) A modified (dual) fusion technique for image encryption using SHA-256 hash and multiple chaotic maps. Multimed Tools Appl 75(18):11241–11266

    Google Scholar 

  37. Liu H, Wang X (2012) Image encryption using DNA complementary rule and chaotic maps. Appl Soft Comput 12(5):1457–1466

    Google Scholar 

  38. Liu L, Zhang Q, Wei X (2012) A RGB image encryption algorithm based on DNA encoding and chaos map. Comput Electric Eng 38(5):1240–1248

    Google Scholar 

  39. Luo Y, Tang S, Liu J, Cao L, Qiu S (2020) Image encryption scheme by combining the hyper-chaotic system with quantum coding. Opt Lasers Eng 124:105836

    Google Scholar 

  40. Mylrea M (2017) Smart energy-internet-of-things opportunities require smart treatment of legal, privacy and cybersecurity challenges. J World Energy Law Business 10(2):147–158

    Google Scholar 

  41. Negou AN, Kengne J (2018) Dynamic analysis of a unique jerk system with a smoothly adjustable symmetry and nonlinearity: reversals of period doubling, offset boosting and coexisting bifurcations. AEU-Int J Electronics Commun 90:1–19

    Google Scholar 

  42. Norouzi B, Seyedzadeh SM, Mirzakuchaki S, Mosavi MR (2015) A novel image encryption based on row-column, masking and main diffusion processes with hyper chaos. Multimed Tools Appl 74(3):781–811

    MATH  Google Scholar 

  43. Pak C, Huang L (2017) A new color image encryption using combination of the 1D chaotic map. Signal Process 138:129–137

    Google Scholar 

  44. Pisarchik A, Zanin M (2008) Image encryption with chaotically coupled chaotic maps. Phys D: Nonlinear Phenom 237(20):2638–2648. https://doi.org/10.1016/j.physd.2008.03.049

  45. Signing VF, Kengne J (2019) Reversal of period-doubling and extreme multistability in a novel 4D chaotic system with hyperbolic cosine nonlinearity. Int J Dynamics Control 7(2):439–451

    MathSciNet  Google Scholar 

  46. Signing VRF, Kengne J, Kana LK (2018) Dynamic analysis and multistability of a novel four-wing chaotic system with smooth piecewise quadratic nonlinearity. Chaos, Solitons Fractals: Interdisciplin J Nonlinear Sci Nonequilibrium Complex Phenomena 113:263–274. https://doi.org/10.1016/j.chaos.2018.06.008

    Article  MathSciNet  MATH  Google Scholar 

  47. Singh JP, Roy B (2016) The nature of Lyapunov exponents is (+,+,−,−). Is it a hyperchaotic system? Chaos, Solitons Fract 92:73–85. https://doi.org/10.1016/j.chaos.2016.09.010

  48. Singh JP, Roy B (2017) The simplest 4-D chaotic system with line of equilibria, chaotic 2-torus and 3-torus behaviour. Nonlinear Dynamics 89(3):1845–1862

    MathSciNet  Google Scholar 

  49. Steven HS (1994) Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Westview press

  50. Su X, Li W, Hu H (2017) Cryptanalysis of a chaos-based image encryption scheme combining DNA coding and entropy. Multimed Tools Appl 76(12):14021–14033

    Google Scholar 

  51. Tenny R, Tsimring LS, Larson L, Abarbanel HD (2003) Using distributed nonlinear dynamics for public key encryption. Phys Rev Lett 90(4):047903

    Google Scholar 

  52. Tsafack N, Kengne J (2018) A novel autonomous 5-d hyperjerk RC circuit with hyperbolic sine function. Sci World J 2018:1–17

    Google Scholar 

  53. Tsafack N, Kengne J, Abd-El-Atty B, Iliyasu AM, Hirota K, Abd El-Latif AA (2020) Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption. Inf Sci 515:191–217. https://doi.org/10.1016/j.ins.2019.10.070

    Article  MATH  Google Scholar 

  54. Rehman A u, Liao X (2019) A novel robust dual diffusion/confusion encryption technique for color image based on Chaos, DNA and SHA-2. Multimed Tools Appl 78(2):2105–2133. https://doi.org/10.1007/s11042-018-6346-1

  55. Vaidyanathan S, Akgul A, Kaçar S, Çavuşoğlu U (2018) A new 4-D chaotic hyperjerk system, its synchronization, circuit design and applications in RNG, image encryption and chaos-based steganography. European Phys J Plus 133(2):1–18

    Google Scholar 

  56. Volos C, Akgul A, Pham V-T, Stouboulos I, Kyprianidis I (2017) A simple chaotic circuit with a hyperbolic sine function and its use in a sound encryption scheme. Nonlinear Dynamics 89(2):1047–1061

    Google Scholar 

  57. Wang X, H-l Z (2016) A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dyn 83(1–2):333–346. https://doi.org/10.1007/s11071-015-2330-8

  58. Wang X, Liu C (2017) A novel and effective image encryption algorithm based on chaos and DNA encoding. Multimed Tools Appl 76(5):6229–6245

    Google Scholar 

  59. Wang Y, Wong K-W, Liao X, Xiang T, Chen G (2009) A chaos-based image encryption algorithm with variable control parameters. Chaos, Solitons Fractals 41(4):1773–1783

    MATH  Google Scholar 

  60. Wang X-Y, Yang L, Liu R, Kadir A (2010) A chaotic image encryption algorithm based on perceptron model. Nonlinear Dynamics 62(3):615–621

    MathSciNet  MATH  Google Scholar 

  61. Wang X-Y, Zhang Y-Q, Bao X-M (2015) A novel chaotic image encryption scheme using DNA sequence operations. Opt Lasers Eng 73:53–61. https://doi.org/10.1016/j.optlaseng.2015.03.022

  62. Wang X, Liu C, Zhang H (2016) An effective and fast image encryption algorithm based on Chaos and interweaving of ranks. Nonlinear Dynamics 84(3):1595–1607

    MathSciNet  MATH  Google Scholar 

  63. Wang X, Wang Y, Zhu X, Unar S (2019) Image encryption scheme based on Chaos and DNA plane operations. Multimed Tools Appl 78(18):26111–26128

    Google Scholar 

  64. Wang X, Xue W, An J (2020) Image encryption algorithm based on LDCML and DNA coding sequence. Multimedia Tools and Applications:1–24

  65. Watson JD, Crick FH (1953) Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid. Nature 171(4356):737–738

    Google Scholar 

  66. Watson JD, Crick F (1953) A structure for deoxyribose nucleic acid.

  67. Wei Z, Zhang W (2014) Hidden hyperchaotic attractors in a modified Lorenz–Stenflo system with only one stable equilibrium. Int J Bifurcation Chaos 24(10):1450127

    MathSciNet  MATH  Google Scholar 

  68. Wei X, Guo L, Zhang Q, Zhang J, Lian S (2012) A novel color image encryption algorithm based on DNA sequence operation and hyper-chaotic system. J Syst Softw 85(2):290–299. https://doi.org/10.1016/j.jss.2011.08.017

  69. Wei Z, Wang R, Liu A (2014) A new finding of the existence of hidden hyperchaotic attractors with no equilibria. Math Comput Simul 100:13–23

    MathSciNet  MATH  Google Scholar 

  70. Wong K-W, Kwok BS-H, Law W-S (2008) A fast image encryption scheme based on chaotic standard map. Phys Lett A 372(15):2645–2652

    MATH  Google Scholar 

  71. Wu X, Kan H, Kurths J (2015) A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps. Appl Soft Comput 37:24–39

    Google Scholar 

  72. Xiao G, Lu M, Qin L, Lai X (2006) New field of cryptography: DNA cryptography. Chin Sci Bull 51(12):1413–1420

    MathSciNet  MATH  Google Scholar 

  73. Xie T, Liu Y, Tang J (2014) Breaking a novel image fusion encryption algorithm based on DNA sequence operation and hyper-chaotic system. Optik 125(24):7166–7169

    Google Scholar 

  74. Yu H, Cai G, Li Y (2012) Dynamic analysis and control of a new hyperchaotic finance system. Nonlinear Dynamics 67(3):2171–2182

    MathSciNet  MATH  Google Scholar 

  75. Yu W, Liu Y, Gong L, Tian M, Tu L (2019) Double-image encryption based on spatiotemporal chaos and DNA operations. Multimed Tools Appl 78(14):20037–20064

    Google Scholar 

  76. Zefreh EZ (2020) An image encryption scheme based on a hybrid model of DNA computing, chaotic systems and hash functions. Multimed Tools Appl 79(33):24993–25022

    Google Scholar 

  77. Zhan K, Wei D, Shi J, Yu J (2017) Cross-utilizing hyperchaotic and DNA sequences for image encryption. J Electronic Imaging 26(1):013021. https://doi.org/10.1117/1.JEI.26.1.013021

  78. Zhang X, Ye R (2020) A novel RGB image encryption algorithm based on DNA sequences and chaos. Multimedia Tools and Applications:1–25

  79. Zhang Q, Guo L, Wei X (2010) Image encryption using DNA addition combining with chaotic maps. Math Comput Model 52(11–12):2028–2035

    MathSciNet  MATH  Google Scholar 

  80. Zhao X, Li Z, Li S (2011) Synchronization of a chaotic finance system. Appl Math Comput 217(13):6031–6039

    MathSciNet  MATH  Google Scholar 

  81. Zhu C-X, Sun K-H (2012) Cryptanalysis and improvement of a class of hyperchaos based image encryption algorithms

  82. Zhu C-X, Hu Y-P, Sun K-H (2012) New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern. Dianzi Yu Xinxi Xuebao(J Electron Inform Technol) 34(7):1735–1743

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Unité de Recherche de Laboratoire d’Automatique et Informatique Appliquée (URAIA), Department of Electrical Engineering, IUT-FV Bandjoun, University of Dschang, Dschang, Cameroon

    V. R. Folifack Signing, R. L. Tagne Mogue & J. Kengne

  2. Unité de Recherche de Matière Condensée, d’Electronique et de Traitement du Signal (URMACETS), Department of Physics, University of Dschang, P.O. Box 67, Dschang, Cameroon

    V. R. Folifack Signing, R. L. Tagne Mogue & M. Kountchou

  3. Research Center for Nuclear Science and Technology, Institute of Geological and Mining Research, P.O. Box 4110, Yaoundé, Cameroon

    V. R. Folifack Signing, R. L. Tagne Mogue, M. Kountchou &  Saïdou

  4. Nuclear Physics Laboratory, Faculty of Science, University of Yaoundé I, P.O. Box 812, Yaoundé, Cameroon

    Saïdou

Authors
  1. V. R. Folifack Signing
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. R. L. Tagne Mogue
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. J. Kengne
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. M. Kountchou
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Saïdou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to V. R. Folifack Signing.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: Preliminary study for system dynamics

1.1 A.1. Study of Dissipativity

The necessary condition to study the dissipation of the system (1) is expressed by the following equation [15, 46]. System (1) can be written as:

$$ \Big\{{\displaystyle \begin{array}{c}{f}_1\left({x}_1,{x}_2,{x}_3,{x}_4\right)={x}_3+{x}_1\left({x}_2-a\right)+{x}_4\\ {}{f}_2\left({x}_1,{x}_2,{x}_3,{x}_4\right)=1-b{x}_2-{x}_1^2\\ {}{f}_3\left({x}_1,{x}_2,{x}_3,{x}_4\right)=-{x}_1-c{x}_3\\ {}{f}_4\left({x}_1,{x}_2,{x}_3,{x}_4\right)=-d{x}_1{x}_2-k{x}_4\end{array}} $$
(A1)

The rate of volume contraction of system (A1) is computed as:

$$ \nabla V=\frac{\partial {f}_1}{\partial {x}_1}+\frac{\partial {f}_2}{\partial {x}_2}+\frac{\partial {f}_3}{\partial {x}_3}+\frac{\partial {f}_4}{\partial {x}_4}={x}_2-\left(a+b+c+k\right) $$
(A2)

1.2 A.2. Equilibrium point

To study the stability of equilibrium point amounts to determine this point which is obtained by solving the system equation \( {\dot{x}}_1={\dot{x}}_2={\dot{x}}_3={\dot{x}}_4=0 \) in order to know if it is stable or unstable. Thus, system (1) has three equilibrium points which are expressed as follows:

$$ {E}_1=\left(0,1/b,0,0\right),{E}_{2,3}=\left(\pm \vartheta, \frac{k\left( ac+1\right)}{c\left(k-d\right)},\mp \frac{\vartheta }{c},\frac{d\vartheta}{c\left(d-k\right)}\left( ca+1\right)\right) $$
(A3)

With \( \vartheta =\frac{\sqrt{dc+ kc ab+ kb+ kc}}{c\left(d-k\right)} \)

The Jacobian matrix of the system (1) around any fixed point E1, E2, or E3 is defined by:

$$ J=\left[\begin{array}{cccc}{x}_2-a& {x}_1& 1& 1\\ {}-2{x}_1& -b& 0& 0\\ {}-1& 0& -c& 0\\ {}-d{x}_2& -d{x}_1& 0& -k\end{array}\right] $$
(A4)

1.3 A.3. Lyapunov dimension

Using the Wolf algorithm [45] and for the range of the system parameters a = 1, b = 0.11, c = 1.04, d = 0.2, and k = 0.17, the four Lyapunov exponents are computed as follows: L1 = 0.0505454, L2 = 0.0166925, L3 = 0, and L1 =  − 0.679484. We find that in these conditions, the system (1) is hyperchaotic because it consists of two positive exponents L1and L2, one null Lyapunov exponent L3, and a negative Lyapunov L4 [47]. We find that, L1 + L2 + L3 = 0.0672379 positive and L1 + L2 + L3 + L4 =  − 0.6122461negative, consequently, the dimension of Kaplan Yorke [69] for this financial hyperchaotic system (1) is found as:

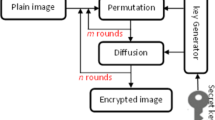
$$ {D}_{KY}=3+\frac{L_1+{L}_2+{L}_3}{\mid {L}_4\mid }=3.098954354 $$
(A5)

Appendix B: Algorithms of the encryption and decryption process

figure a
figure b
figure c
figure d
figure e

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Signing, V.R.F., Mogue, R.L.T., Kengne, J. et al. Dynamic phenomena of a financial hyperchaotic system and DNA sequences for image encryption. Multimed Tools Appl 80, 32689–32723 (2021). https://doi.org/10.1007/s11042-021-11180-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-021-11180-9

Keywords