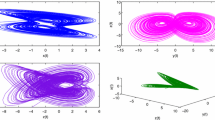
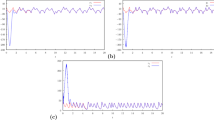
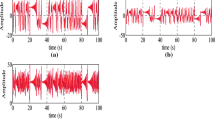
Abstract
Synchronization of different Chaotic dynamical systems is one of the main issues in engineering which has a lot of applications in applied sciences like secure communications and cryptography. In this work, a chattering-free fractional-integral-based sliding mode control (SMC) methodology is proposed for the synchronization of different chaotic fractional-order systems with input saturation. Based on the frequency distributed model and the non-integer version of the Lyapunov stability theorem and using a new continuous function instead of sign function, a novel model-free SMC (MFSMC) method is proposed to overcome the chaotic behavior of the FOSs without any undesired chattering phenomenon. In addition, utilizing the boundedness property of the fractional-order chaotic system is caused to design the method. Then, by operating the proposed scheme on chaotic fractional-order systems, which are applied in electrical systems and secure communications, the effectiveness and applicability of the MFSMC are validated. After that, to show the real-world application, a novel encryption/decryption method for color images is introduced based on the proposed MFSMC. According to an adaption of the pre-diffusion-permutation-diffusion, the structure is adopted to improve the level of security. Furthermore, the performance and security analyses are given to confirm the superiority of the proposed encryption scheme, including histogram analysis, adjacent pixel correlation analysis, and information entropy analysis.













Similar content being viewed by others
References
Aghababa MP (2012) Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique. Nonlinear Dynamics 69(1–2):247–261
Aghababa MP (2017) Stabilization of a class of fractional-order chaotic systems using a non-smooth control methodology. Nonlinear Dynamics 89(2):1357–1370
Aghababa MP, Borjkhani M (2014) Chaotic fractional-order model for muscular blood vessel and its control via fractional control scheme. Complexity 20(2):37–46
Aghababa MP, Moradi S (2020) Robust adaptive dynamic surface back-stepping tracking control of high-order strict-feedback nonlinear systems via disturbance observer approach. Int J Control 94(9):2479–2495
Aghababa MP, Saif M (2020) Adaptive control realization for canonic Caputo fractional-order systems with actuator nonlinearity: application to mechatronic devices. Advances in Difference Equations 2020(1):372. https://doi.org/10.1186/s13662-020-02829-0
Aghababa MP, Haghighi AR, Roohi M (2015) Stabilisation of unknown fractional-order chaotic systems: an adaptive switching control strategy with application to power systems. IET Generation, Transmission & Distribution 9(14):1883-1893.
Ahmad WM, El-Khazali RJC (2007) Fractional-order dynamical models of love. Solitons, Fractals 33(4):1367–1375
Argyris A, Syvridis D, Larger L, Annovazzi-Lodi V, Colet P, Fischer I, Garcia-Ojalvo J, Mirasso CR, Pesquera L, Shore KA (2005) Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 438(7066):343–346. https://doi.org/10.1038/nature04275
Asgharnia A, Jamali A, Shahnazi R, Maheri A (2020) Load mitigation of a class of 5-MW wind turbine with RBF neural network based fractional-order PID controller. ISA Trans 96:272–286. https://doi.org/10.1016/j.isatra.2019.07.006
Asl MS, Javidi M (2017) An improved PC scheme for nonlinear fractional differential equations: error and stability analysis. J Comput Appl Math 324:101–117. https://doi.org/10.1016/j.cam.2017.04.026
Babes B, Boutaghane A, Hamouda N, Mezaache M (2019) Design of a Voltage Controller for a DC-DC Buck Converter Using Fractional-Order Terminal Sliding Mode Control Strategy. In: International Conference on Advanced Electrical Engineering 2019 (ICAEE 2019)
Babu NR, Kalpana M, Balasubramaniam P (2021) A novel audio encryption approach via finite-time synchronization of fractional order hyperchaotic system. Multimed Tools Appl 80(12):18043–18067. https://doi.org/10.1007/s11042-020-10288-8
Balamash A, Bettayeb M, Djennoune S, Al-Saggaf U, Moinuddin M (2020) Fixed-time terminal synergetic observer for synchronization of fractional-order chaotic systems. Chaos 30(7):073124
Balasubramaniam P, Muthukumar P, Ratnavelu K (2015) Theoretical and practical applications of fuzzy fractional integral sliding mode control for fractional-order dynamical system. Nonlinear Dynamics 80(1):249–267. https://doi.org/10.1007/s11071-014-1865-4
Cai W, Wang P, Fan J (2020) A variable-order fractional model of tensile and shear behaviors for sintered nano-silver paste used in high power electronics. Mech Mater 145:103391. https://doi.org/10.1016/j.mechmat.2020.103391
Caponetto R, Pasquale GD, Graziani S, Murgano E, Pollicino A, Trigona C (2020) Green Fractional Order Elements Based on Bacterial Cellulose and Ionic Liquids. In: 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), 25–28 May 2020, pp 1–6
Chen C, Ding Z (2019) Projective Synchronization of Nonidentical Fractional-Order Memristive Neural Networks. Discrete Dynamics in Nature and Society: 8743482
Chen Y, Tang C, Yi Z (2020) A novel image encryption scheme based on PWLCM and standard map. Complexity: 3026972
Chen Y, Tang C, Ye R (2020) Cryptanalysis and improvement of medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Processing 167. https://doi.org/10.1016/j.sigpro.2019.107286
Chen Y, Tang C, Roohi M (2021) Design of a model-free adaptive sliding mode control to synchronize chaotic fractional-order systems with input saturation: an application in secure communications. Journal of the Franklin Institute 358(16):8109–8137. https://doi.org/10.1016/j.jfranklin.2021.08.007
Cohen I, Golding I, Ron I, Ben-Jacob (2001) Biofluiddynamics of lubricating bacteria. Math Method Appl Sci 24(17–18):1429–1468
Curran PF, Chua LO (1997) Absolute stability theory and the synchronization problem. International Journal of Bifurcation and Chaos 07(06):1375–1382. https://doi.org/10.1142/s0218127497001096
Diethelm K (2013) A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dynamics 71(4):613–619. https://doi.org/10.1007/s11071-012-0475-2
Diethelm K, Ford NJ, Freed A (2002) A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dynamics 29(1):3–22. https://doi.org/10.1023/a:1016592219341
Djimasra F, Nkapkop JDD, Tsafack N, Kengne J, Effa JY, Boukabou A, Bitjoka L (2021) Robust cryptosystem using a new hyperchaotic oscillator with stricking dynamic properties. Multimed Tools Appl 80(16):25121–25137. https://doi.org/10.1007/s11042-021-10734-1
Doubla IS, Njitacke ZT, Ekonde S, Tsafack N, Nkapkop JDD, Kengne J (2021) Multistability and circuit implementation of tabu learning two-neuron model: application to secure biomedical images in IoMT. Neural Comput Appl:1–29. https://doi.org/10.1007/s00521-021-06130-3
Esfahani Z, Roohi M, Gheisarnejad M, Dragičević T, Khooban M-H (2019) Optimal non-integer sliding mode control for frequency regulation in stand-alone modern power grids. Appl Sci 9(16):3411
Fradkov AL, Evans RJ (2005) Control of chaos: methods and applications in engineering. Annu Rev Control 29(1):33–56. https://doi.org/10.1016/j.arcontrol.2005.01.001
Haghighi A, Ziaratban R (2020) A non-integer sliding mode controller to stabilize fractional-order nonlinear systems. Advances in Difference Equations 2020(1):503. https://doi.org/10.1186/s13662-020-02954-w
Javan AAK, Jafari M, Shoeibi A, Zare A, Khodatars M, Ghassemi N, Alizadehsani R, Gorriz JM (2021) Medical images encryption based on adaptive-robust multi-mode synchronization of Chen hyper-chaotic systems. Sensors (Basels) 21(11):3925. https://doi.org/10.3390/s21113925
Jia H-Y, Chen Z-Q, Qi G-Y (2013) Topological horseshoe analysis and circuit realization for a fractional-order Lü system. Nonlinear Dynamics 74(1–2):203–212
Kekha Javan AA, Shoeibi A, Zare A, Hosseini Izadi N, Jafari M, Alizadehsani R, Moridian P, Mosavi A, Acharya UR, Nahavandi S (2021) Design of Adaptive-Robust Controller for multi-state synchronization of chaotic systems with unknown and time-varying delays and its application in secure communication. Sensors 21(1):254
Khan A, Jahanzaib LS (2019) Synchronization on the adaptive sliding mode controller for fractional order complex chaotic systems with uncertainty and disturbances. International Journal of Dynamics and Control 7(4):1419–1433
Laskin NJPRE (2002) Fractional schrödinger equation. 66(5):056108
Li C, Chen G (2004) Chaos in the fractional order Chen system and its control. Chaos, Solitons Fractals 22(3):549–554. https://doi.org/10.1016/j.chaos.2004.02.035
Li C, Deng W (2007) Remarks on fractional derivatives. Appl Math Comput 187(2):777–784. https://doi.org/10.1016/j.amc.2006.08.163
Li R-G, Wu H-N (2019) Adaptive synchronization control with optimization policy for fractional-order chaotic systems between 0 and 1 and its application in secret communication. ISA Trans 92:35–48. https://doi.org/10.1016/j.isatra.2019.02.027
Li Y, Chen Y, Podlubny I (2010) Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Computers & Mathematics with Applications 59(5):1810–1821. https://doi.org/10.1016/j.camwa.2009.08.019
Li Y, Wang H, Tian Y (2019) Fractional-order adaptive controller for chaotic synchronization and application to a dual-channel secure communication system. Modern Physics Letters B 33(24):1950290. https://doi.org/10.1142/s0217984919502907
Li G, Zhang X, Yang HJIA (2020) Complexity analysis and synchronization control of fractional-order jafari-sprott chaotic system. IEEE Access 8:53360–53373
Liu X, Yu Y (2021) Synchronization analysis for discrete fractional-order complex-valued neural networks with time delays. Neural Comput & Applic 33(16):10503–10514. https://doi.org/10.1007/s00521-021-05808-y
Lu JG (2006) Chaotic dynamics of the fractional-order Lü system and its synchronization. Phys Lett A 354(4):305–311
Luo S, Lewis FL, Song Y, Vamvoudakis KG (2020) Adaptive backstepping optimal control of a fractional-order chaotic magnetic-field electromechanical transducer. Nonlinear Dynamics 100(1):523–540. https://doi.org/10.1007/s11071-020-05518-5
Modiri A, Mobayen S (2020) Adaptive terminal sliding mode control scheme for synchronization of fractional-order uncertain chaotic systems. ISA Trans 105:33–50. https://doi.org/10.1016/j.isatra.2020.05.039
Mofid O, Mobayen S, Khooban MH (2019) Sliding mode disturbance observer control based on adaptive synchronization in a class of fractional-order chaotic systems. Int J Adapt Control Signal Process 33(3):462–474
Mohadeszadeh M, Pariz N (2019) Hybrid control of synchronization of fractional-order nonlinear systems. Asian J Control 23(1):412-422
Moon S, Baik J-J, Seo JM (2021) Chaos synchronization in generalized Lorenz systems and an application to image encryption. Communications in Nonlinear Science and Numerical Simulation 96:105708. https://doi.org/10.1016/j.cnsns.2021.105708
Muñoz-Guillermo M (2021) Image encryption using q-deformed logistic map. Inf Sci 552:352–364. https://doi.org/10.1016/j.ins.2020.11.045
Muthukumar P, Balasubramaniam P, Ratnavelu K (2017) A novel cascade encryption algorithm for digital images based on anti-synchronized fractional order dynamical systems. Multimed Tools Appl 76(22):23517–23538. https://doi.org/10.1007/s11042-016-4052-4
Muthukumar P, Balasubramaniam P, Ratnavelu K (2017) Sliding mode control design for synchronization of fractional order chaotic systems and its application to a new cryptosystem. International Journal of Dynamics and Control 5(1):115–123. https://doi.org/10.1007/s40435-015-0169-y
Nassajian G, Balochian S (2020) Optimal control based on neuro estimator for fractional order uncertain non-linear continuous-time systems. Neural Process Lett 52(1):221–240. https://doi.org/10.1007/s11063-020-10261-4
Njitacke ZT, Isaac SD, Nestor T, Kengne J (2020) Window of multistability and its control in a simple 3D Hopfield neural network: application to biomedical image encryption. Neural Comput Appl 33:6733–6752. https://doi.org/10.1007/s00521-020-05451-z
Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier Science
Rajagopal K, Jahanshahi H, Jafari S, Weldegiorgis R, Karthikeyan A, Duraisamy P Coexisting attractors in a fractional-order hydro-turbine governing system and fuzzy PID based chaos control. Asian J Control 23(4):1–14. https://doi.org/10.1002/asjc.2261
Roohi M, Aghababa MP, Haghighi AR (2015) Switching adaptive controllers to control fractional-order complex systems with unknown structure and input nonlinearities. Complexity 21(2):211–223.
Roohi M, Khooban M-H, Esfahani Z, Aghababa MP, Dragicevic T (2019) A switching sliding mode control technique for chaos suppression of fractional-order complex systems. Trans Inst Meas Control 41(10):2932–2946. https://doi.org/10.1177/0142331219834606
Roohi M, Zhang C, Chen Y (2020) Adaptive model-free synchronization of different fractional-order neural networks with an application in cryptography. Nonlinear Dynamics 100(4):3979–4001. https://doi.org/10.1007/s11071-020-05719-y
Sabzalian MH, Mohammadzadeh A, Lin S, Zhang W (2019) Robust fuzzy control for fractional-order systems with estimated fraction-order. Nonlinear Dynamics 98:2375–2385.https://doi.org/10.1007/s11071-019-05217-w
Shao K, Xu Z, Wang T (2020) Robust finite-time sliding mode synchronization of fractional-order hyper-chaotic systems based on adaptive neural network and disturbances observer. Int J Dyn Control 9:541–549
Shirkavand M, Pourgholi M (2018) Robust fixed-time synchronization of fractional-order chaotic using free chattering nonsingular adaptive fractional sliding mode controller design. Chaos, Solitons Fractals 113:135–147
Song L, Xu S, Yang JJ (2010) Dynamical models of happiness with fractional order. Communications in Nonlinear Science and Numerical Simulation 15(3):616–628
Song X, Song S, Balsera IT, Liu L, Zhang L (2017) Synchronization of two fractional-order chaotic systems via nonsingular terminal fuzzy sliding mode control. J Control Sci Eng 9562818
Song S, Park JH, Zhang B, Song X, Zhang Z (2021) Adaptive command filtered neuro-fuzzy control design for fractional-order nonlinear systems with unknown control directions and input quantization. IEEE Transactions on Systems, Man, and Cybernetics: Systems 51(11):7238–7249. https://doi.org/10.1109/TSMC.2020.2967425
Sun Z (2018) Synchronization of fractional-order chaotic systems with non-identical orders, unknown parameters, and disturbances via sliding mode control. Chin J Phys 56(5):2553–2559
Sun H, Zhang Y, Baleanu D, Chen W, Chen Y (2018) A new collection of real world applications of fractional calculus in science and engineering. Commun Nonlinear Sci Numer Simul 64:213–231. https://doi.org/10.1016/j.cnsns.2018.04.019
Tang X, Zhai D, Fu Z, Wang H (2020) Output feedback adaptive fuzzy control for uncertain fractional-order nonlinear switched system with output quantization. International Journal of Fuzzy Systems 22(3):943–955. https://doi.org/10.1007/s40815-020-00814-z
Tsafack N, Sankar S, Abd-El-Atty B, Kengne JCJK, Belazi A, Mehmood I, Bashir AK, Song O-Y, El-Latif AAA (2020) A new chaotic map with dynamic analysis and encryption application in internet of health things. IEEE Access 8:137731–137744. https://doi.org/10.1109/access.2020.3010794
Vafamand N, Khorshidi S (2018) Robust polynomial observer-based chaotic synchronization for Non-Ideal Channel secure communication: an SOS approach. Iranian Journal of Science and Technology, Transactions of Electrical Engineering 42(1):83–94. https://doi.org/10.1007/s40998-018-0047-7
Vafamand N, Khorshidi S, Khayatian A (2018) Secure communication for non-ideal channel via robust TS fuzzy observer-based hyperchaotic synchronization. Chaos, Solitons Fractals 112:116–124. https://doi.org/10.1016/j.chaos.2018.04.035
Wang B, Ding J, Wu F, Zhu D (2016) Robust finite-time control of fractional-order nonlinear systems via frequency distributed model. Nonlinear Dynamics 85(4):2133–2142. https://doi.org/10.1007/s11071-016-2819-9
Wang J, Han K, Fan S, Zhang Y, Tan H, Jeon G, Pang Y, Lin J (2020) A logistic mapping-based encryption scheme for wireless body area networks. Futur Gener Comput Syst 110:57–67
Weitzner H, Zaslavsky GJ (2003) Some applications of fractional equations. Commun Nonlinear Sci Numer Simul 8(3–4):273–281
Xue W, Li Y, Cang S, Jia H, Wang Z (2015) Chaotic behavior and circuit implementation of a fractional-order permanent magnet synchronous motor model. J Franklin Institute 352(7):2887–2898
Yan Y, Kou C (2012) Stability analysis for a fractional differential model of HIV infection of CD4+ T-cells with time delay. Math Comput Simul 82(9):1572–1585
Yin C, Dadras S, Zhong, S.-m. (2012) Design an adaptive sliding mode controller for drive-response synchronization of two different uncertain fractional-order chaotic systems with fully unknown parameters. Journal of the Franklin Institute 349(10):3078–3101. https://doi.org/10.1016/j.jfranklin.2012.09.009
Zhang L, Zhong J, Lu J (2021) Intermittent control for finite-time synchronization of fractional-order complex networks. Neural Netw 144:11–20. https://doi.org/10.1016/j.neunet.2021.08.004
Zhao C-F, Ren H-P (2020) Image encryption based on hyper-chaotic multi-attractors. Nonlinear Dynamics 100(1):679–698. https://doi.org/10.1007/s11071-020-05526-5
Zhou P, Bai R-j, Zheng J-m (2015) Stabilization of a fractional-order chaotic brushless DC motor via a single input. Nonlinear Dynamics 82(1–2):519–525
Zouad F, Kemih K, Hamiche H (2019) A new secure communication scheme using fractional order delayed chaotic system: design and electronics circuit simulation. Analog Integr Circ Sig Process 99(3):619–632. https://doi.org/10.1007/s10470-018-01382-x
Acknowledgments
This work is supported by the National Nature Sciences Foundation of China (Grant No. 12071096).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
the authors declare that they have no conflict of interest related the publication of this manuscript.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Taheri, M., Zhang, C., Berardehi, Z.R. et al. No-chatter model-free sliding mode control for synchronization of chaotic fractional-order systems with application in image encryption. Multimed Tools Appl 81, 24167–24197 (2022). https://doi.org/10.1007/s11042-022-12329-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-022-12329-w