Skip to main content
Springer Nature Link
Log in

Multi-view clustering via dual-norm and HSIC

  • 1230: Sentient Multimedia Systems and Visual Intelligence
  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

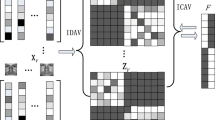
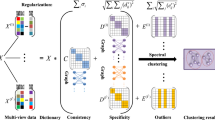
Fully capturing valid complementary information in multi-view data enhances the connection between similar data points and weakens the correlation between different data point categories. In this paper, we propose a new multi-view clustering via dual-norm and Hilbert-Schmidt independence criterion (HSIC) induction (MCDHSIC) approach, which can enhance the complementarity, reduce the redundancy between multi-view representations, and improve the accuracy of the clustering results. This model uses the HSIC as the diversity regularization term to capture the nonlinear relationship between different views. In addition, l1-norm and Frobenius norm constraints are imposed to obtain a subspace representation matrix with inter-class sparsity and intra-class consistency. Moreover, we also designed a valuable approach to optimizing the proposed model and theoretically analyzing the convergence of the MCDHSIC method. The results of extensive experiments conducted on five challenging data sets show that the proposed method objectively achieves a highly competent performance compared with several other state-of-the-art multi-view clustering methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Avants BB, Tustison NJ, Stone JR (2021) Similarity-driven multi-view embeddings from high-dimensional biomedical data. Nat Comput Sci 1(2):143–152. https://doi.org/10.1038/s43588-021-00029-8

    Article  Google Scholar 

  2. Bartels RH, Stewart GW (1972) Solution of the matrix equation AX+ XB= C [F4]. Commun ACM 15(9):820–826. https://doi.org/10.1145/361573.361582

    Article  Google Scholar 

  3. Brbić M, Kopriva I (2018) Multi-view low-rank sparse subspace clustering. Pattern Recogn 73:247–258. https://doi.org/10.1016/j.patcog.2017.08.024

    Article  Google Scholar 

  4. Cao X, Zhang C, Fu H et al (2015) Diversity-induced multi-view subspace clustering. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 586–594

  5. Chauhan S, Singh M, Aggarwal AK (2020) An effective health indicator for bearing using corrected conditional entropy through diversity-driven multi-parent evolutionary algorithm. Struct Health Monit 1475921720962419. https://doi.org/10.1177/1475921720962419

  6. Chauhan S, Singh M, Aggarwal AK (2021) Cluster head selection in heterogeneous wireless sensor network using a new evolutionary algorithm. Wirel Pers Commun 119(1):585–616. https://doi.org/10.1007/s11277-021-08225-5

    Article  Google Scholar 

  7. Chauhan S, Singh M, Aggarwal AK (2021) Design of a two-channel quadrature mirror filter bank through a diversity-driven multi-parent evolutionary algorithm. Circuits Syst Signal Process 40(7):3374–3394. https://doi.org/10.1007/s00034-020-01625-1

    Article  Google Scholar 

  8. Chen MS, Huang L, Wang CD, Huang D, Lai JH (2021) Relaxed multi-view clustering in latent embedding space. Inf Fusion 68:8–21. https://doi.org/10.1016/j.inffus.2020.10.013

    Article  Google Scholar 

  9. De Sa VR (2005) Spectral clustering with two views. In: ICML workshop on learning with multiple views, pp. 20–27

  10. Elhamifar E, Vidal R (2013) Sparse subspace clustering: algorithm, theory, and applications. IEEE Trans Pattern Anal Mach Intell 35(11):2765–2781. https://doi.org/10.1109/TPAMI.2013.57

    Article  Google Scholar 

  11. Gretton A, Bousquet O, Smola A, Schölkopf B (2005) Measuring statistical dependence with Hilbert-Schmidt norms. In: International conference on algorithmic learning theory. Springer, Berlin, Heidelberg, pp. 63–77

  12. Hu H, Lin Z, Feng J et al (2014) Smooth representation clustering. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 3834–3841

  13. Hu J, Zhou XG, Zhu YH, Yu DJ, Zhang GJ (2019) TargetDBP: accurate DNA-binding protein prediction via sequence-based multi-view feature learning. IEEE/ACM Trans Comput Biol Bioinform 17(4):1419–1429. https://doi.org/10.1109/TCBB.2019.2893634

    Article  Google Scholar 

  14. Hu Z, Nie F, Chang W, Hao S, Wang R et al (2020) Multi-view spectral clustering via sparse graph learning. Neurocomputing 384:1–10. https://doi.org/10.1016/j.neucom.2019.12.004

    Article  Google Scholar 

  15. Huang A, Zhao T, Lin CW (2020) Multi-view data fusion oriented clustering via nuclear norm minimization. IEEE Trans Image Process 29:9600–9613. https://doi.org/10.1109/TIP.2020.3029883

    Article  MathSciNet  Google Scholar 

  16. Hussain SF, Khan M, Siddiqi I (2022) Co-clustering based classification of multi-view data. Appl Intell 52:14756–14772. https://doi.org/10.1007/s10489-021-03087-7

    Article  Google Scholar 

  17. Jolliffe IT (2002) Principal component analysis. J Mark Res 87(4):513. https://doi.org/10.2307/3172953

    Article  Google Scholar 

  18. Kumar A, Daumé H (2011) A co-training approach for multi-view spectral clustering. In: Proceedings of the 28th international conference on machine learning, pp 393-400

  19. Lades M, Vorbruggen JC, Buhmann J, Lange J, von der Malsburg C, Wurtz RP, Konen W (1993) Distortion invariant object recognition in the dynamic link architecture. IEEE Trans Comput 42(3):300–311. https://doi.org/10.1109/12.210173

    Article  Google Scholar 

  20. Lee DD, Seung HS (1999) Learning the parts of objects by non-negative matrix factorization. Nature 401(6755):788–791. https://doi.org/10.1038/44565

    Article  Google Scholar 

  21. Li Z, Tang J, He X (2017) Robust structured nonnegative matrix factorization for image representation. IEEE Trans Neural Netw Learn Syst 29(5):1947–1960. https://doi.org/10.1109/TNNLS.2017.2691725

    Article  MathSciNet  Google Scholar 

  22. Li Z, Tang J, Mei T (2018) Deep collaborative embedding for social image understanding. IEEE Trans Pattern Anal Mach Intell 41(9):2070–2083. https://doi.org/10.1109/TPAMI.2018.2852750

    Article  Google Scholar 

  23. Lu CY, Min H, Zhao ZQ et al (2012) Robust and efficient subspace segmentation via least squares regression. In: European conference on computer vision. Springer, Berlin, Heidelberg, pp. 347–360

  24. Lu GF, Li H, Wang Y, Tang G (2021) Multi-view subspace clustering with Kronecker-basis-representation-based tensor sparsity measure. Mach Vis Appl 32(6):1–12. https://doi.org/10.1007/s00138-021-01247-w

    Article  Google Scholar 

  25. Ng AY, Jordan MI, Weiss Y (2002) On spectral clustering: analysis and an algorithm. In: Proceedings of the neural information processing systems, pp 849–856

  26. Ojala T, Pietikainen M, Maenpaa T (2002) Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans Pattern Anal Mach Intell 24(7):971–987. https://doi.org/10.1109/TPAMI.2002.1017623

    Article  Google Scholar 

  27. Pan G, Xiao L, Bai Y, Wilson TW, Stephen JM, Calhoun VD, Wang YP (2020) Multiview diffusion map improves prediction of fluid intelligence with two paradigms of fMRI analysis. IEEE Trans Biomed Eng 68(8):2529–2539. https://doi.org/10.1109/TBME.2020.3048594

    Article  Google Scholar 

  28. Sun Y, Li L, Zheng L, Hu J, Li W, Jiang Y, Yan C (2019) Image classification base on PCA of multi-view deep representation. J Vis Commun Image Represent 62:253–258. https://doi.org/10.1016/j.jvcir.2019.05.016

    Article  Google Scholar 

  29. Turk M, Pentland A (1991) Eigenfaces for recognition. J Cogn Neurosci 3(1):71–86. https://doi.org/10.1162/jocn.1991.3.1.71

    Article  Google Scholar 

  30. Tzortzis G, Likas A (2012) Kernel-based weighted multi-view clustering. In: 2012 IEEE 12th international conference on data mining, pp 675-684

  31. Van der Maaten L, Hinton G (2008) Visualizing data using t-SNE. J Mach Learn Res 9(2605):2579–2605

  32. van Loon W, Fokkema M, Szabo B, de Rooij M (2020) Stacked penalized logistic regression for selecting views in multi-view learning. Inf Fusion 61:113–123. https://doi.org/10.1016/j.inffus.2020.03.007

    Article  Google Scholar 

  33. Wang H, Weng C, Yuan J (2014) Multi-feature spectral clustering with minimax optimization. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 4106–4113

  34. Wang H, Yang Y, Liu B (2019) GMC: graph-based multi-view clustering. IEEE Trans Knowl Data Eng 32(6):1116–1129. https://doi.org/10.1109/TKDE.2019.2903810

    Article  Google Scholar 

  35. Wang S, Chen Y, Yi S, Chao G (2022) Frobenius norm-regularized robust graph learning for multi-view subspace clustering. Appl Intell 52:14935–14948. https://doi.org/10.1007/s10489-022-03816-6

    Article  Google Scholar 

  36. Wang X, Fu L, Zhang Y, Wang Y et al (2022) MMatch: semi-supervised discriminative representation learning for multi-view classification. IEEE Trans Circuits Syst Video Technol 32:6425–6436. https://doi.org/10.1109/TCSVT.2022.3159371

    Article  Google Scholar 

  37. Xu Y, Wei M (2021) Multi-view clustering toward aerial images by combining spectral analysis and local refinement. Futur Gener Comput Syst 117:138–144. https://doi.org/10.1016/j.future.2020.11.005

    Article  Google Scholar 

  38. Yin Q, Wu S, He R, Wang L (2015) Multi-view clustering via pairwise sparse subspace representation. Neurocomputing 156:12–21. https://doi.org/10.1016/j.neucom.2015.01.017

    Article  Google Scholar 

  39. Zhang C, Fu H, Liu S et al (2015) Low-rank tensor constrained multi-view subspace clustering. In: Proceedings of the IEEE international conference on computer vision, pp. 1582–1590

  40. Zhang C, Hu Q, Fu H et al (2017) Latent multi-view subspace clustering. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 4279–4287

  41. Zhang C, Cheng J, Tian Q (2019) Multi-view image classification with visual, semantic and view consistency. IEEE Trans Image Process 29:617–627. https://doi.org/10.1109/TIP.2019.2934576

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

The National Natural Science Foundation of China under Grants 61806006, China Postdoctoral Science Foundation under Grant No. 2019 M660149, the 111 Project under Grants No. B12018, and PAPD of Jiangsu Higher Education Institutions support this work. Guoqing Liu: Conceptualization, Methodology, Validation, Software, Formal analysis, Data curation, Investigation, Writing–original draft. Hongwei Ge: Resources, Review, Supervision, Project administration, Funding acquisition. Shuzhi Su: Review. Shuangxi Wang: Software, Visualization.

Author information

Authors and Affiliations

  1. School of Artificial Intelligence and Computer Science, Jiangnan University, Wuxi, 214122, Jiangsu, China

    Guoqing Liu, Hongwei Ge & Shuangxi Wang

  2. Key Laboratory of Advanced Process Control for Light Industry, Jiangnan University, Ministry of Education, Wuxi, 214122, China

    Guoqing Liu, Hongwei Ge & Shuangxi Wang

  3. School of Computer Science and Engineering, Anhui University of Science & Technology, Huainan, 232001, Anhui, China

    Shuzhi Su

Authors
  1. Guoqing Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hongwei Ge
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shuzhi Su
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Shuangxi Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hongwei Ge.

Ethics declarations

Competing interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, G., Ge, H., Su, S. et al. Multi-view clustering via dual-norm and HSIC. Multimed Tools Appl 83, 36399–36418 (2024). https://doi.org/10.1007/s11042-022-14057-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-022-14057-7

Keywords