Skip to main content
SpringerLink
Log in

Improving fuzzy clustering model for probability density functions using the two-objective genetic algorithm

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

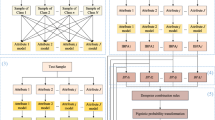
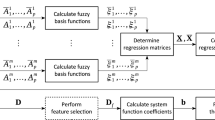
This paper proposes a fuzzy clustering model for probability density functions (PDFs) using the two-objective genetic algorithm. In this model, the \(L^1\)-distance is used to evaluate the similarity of PDFs, and new two indexes that relate to the similarity of PDFs and clusters are proposed as the objective functions of genetic algorithm. Moreover, the operators for crossover, mutation, and selection are also updated to improve the quality of fuzzy clustering according to the corrected rand, the partition entropy, and the partition coefficients. By combining these improvements, we have an effective automatic fuzzy clustering algorithm for PDFs that can determine the appropriate number of clusters, the elements in each cluster, and the probability belonging to clusters of each element. The proposed model is tested through experiments using the established Matlab procedure, and it is also applied effectively to image data. These experiments demonstrate the superiority of the proposed model compared to other models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Data Availability

The authors declare that data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Assunção MD, Calheiros RN, Bianchi S, Netto MA, Buyya R (2015) Big data computing and clouds: trends and future directions. J Parallel Distrib Comput 79:3–15

  2. Bezdek JC (1974) Numerical taxonomy with fuzzy sets. J Math Biol 1(1):57–71

    Article  MathSciNet  Google Scholar 

  3. Bezdek JC (1973) Cluster validity with fuzzy sets. J Cybern 3(3):58–73

    Article  MathSciNet  Google Scholar 

  4. Chehouri A, Younes R, Khoder J, Perron J, Ilinca A (2017) A selection process for genetic algorithm using clustering analysis. Algorithms 10(4):123

    Article  MathSciNet  Google Scholar 

  5. Chen JH, Chang Y, Hung W (2018) A robust automatic clustering algorithm for probability density functions with application to categorizing color images. Commun Stat Simul Comput 47(7):2152–2168

    Article  MathSciNet  Google Scholar 

  6. Chen JH, Hung WL (2015) An automatic clustering algorithm for probability density functions. J Stat Comput Simul 85(15):3047–3063

    Article  MathSciNet  Google Scholar 

  7. Chen Y, Zhou A (2022) Multiobjective portfolio optimization via Pareto front evolution. Complex Intell Syst 8:4301–4317

    Article  Google Scholar 

  8. Davies DL, Bouldin DW (1979) A Cluster Separation Measure. In: IEEE Transactions on Pattern Analysis and Machine Intelligence 1(2):224–227

  9. Diem HK, Trung VD, Trung NT, Van Tai V, Thao NT (2018) A differential evolution-based clustering for probability density functions. IEEE Access 6:41325–41336

    Article  Google Scholar 

  10. Ezugwu AE, Ikotun AM, Oyelade OO, Abualigah L, Agushaka JO, Eke CI, Akinyelu AA (2022) A comprehensive survey of clustering algorithms: State-of-the-art machine learning applications, taxonomy, challenges, and future research prospects. Eng Appl Artif Intell 110:104743

    Article  Google Scholar 

  11. Guo L, Dai Q (2022) Graph clustering via variational graph embedding. Pattern Recogn 122:108334

    Article  Google Scholar 

  12. Holland JH (1973) Genetic algorithms and the optimal allocation of trials. SIAM J Comput 2(2):88–105

    Article  MathSciNet  Google Scholar 

  13. Hubert L (1977) Nominal scale response agreement as a generalized correlation. Br J Math Stat Psychol 30(1):98–103

    Article  Google Scholar 

  14. Hubert L, Arabie P (1985) Comparing partitions. J Classif 2(1):193–218

    Article  Google Scholar 

  15. Hung WL, Yang JH Shen KF (2016) Self-updating clustering algorithm for interval-valued data. In: 2016 IEEE International Conference on Fuzzy Systems, pp 1494–1500

  16. Hussain W, Merigó JM, Raza MR, Gao H (2022) A new qos prediction model using hybrid iowa-anfis with fuzzy c-means, subtractive clustering and grid partitioning. Inf Sci 584:280–300

    Article  Google Scholar 

  17. Kordos M, Blachnik M, Scherer R (2022) Fuzzy clustering decomposition of genetic algorithm-based instance selection for regression problems. Inf Sci 587:23–40

    Article  Google Scholar 

  18. Lotf JJ, Azgomi MA, Dishabi MRE (2022) An improved influence maximization method for social networks based on genetic algorithm. Physica A: Stat Mech Appl 586:126480

    Article  Google Scholar 

  19. Mirkin B, Chernyi L (1970) Measurement of the distance between distinct partitions of a finite set of objects. Avtomatika i Telemekhanika 5:120–127

    MathSciNet  Google Scholar 

  20. Negi SS, Schein CH, Braun W (2022) Regional and temporal coordinated mutation patterns in sars-cov-2 spike protein revealed by a clustering and network analysis. Sci Rep 12(1):1–10

    Article  Google Scholar 

  21. Nguyentrang T, Vovan T (2017) Fuzzy clustering of probability density functions. J Appl Stat 44(4):583–601

    Article  MathSciNet  Google Scholar 

  22. Peiravi A, Nourelfath M, Zanjani MK (2022) Redundancy strategies assessment and optimization of k-out-of-n systems based on markov chains and genetic algorithms. Reliab Eng Syst Saf 221:108277

    Article  Google Scholar 

  23. Phamtoan D, Vovan T, Phamchau A, Nguyentrang T, Hokieu D (2019) A new binary adaptive elitist differential evolution based automatic k-medoids clustering for probability density functions. Math Probl Eng, ID 6380568:1–26

    Google Scholar 

  24. Phamtoan D, Vovan T (2021) Automatic fuzzy genetic algorithm in clustering for images based on the extracted intervals. Multimed Tools Appl 80:35193–35215

    Article  Google Scholar 

  25. Phamtoan D, Nguyenhuu T, Vovan T (2022) Fuzzy clustering algorithm for outlier-interval data based on the robust exponent distance. Appl Intell 52:6276–6291

    Article  Google Scholar 

  26. Phamtoan D, Vovan T (2022) Automatic fuzzy clustering for probability density functions using the genetic algorithm. Neural Comput Appl 34:14609–14625

    Article  Google Scholar 

  27. Phamtoan D, Vovan T (2023) The fuzzy cluster analysis for interval value using genetic algorithm and its application in image recognition. Comput Stat 38:25–51

    Article  MathSciNet  Google Scholar 

  28. Ramezanpour MR, Farajpour M (2022) Application of artificial neural networks and genetic algorithm to predict and optimize greenhouse banana fruit yield through nitrogen, potassium and magnesium. Plos One 17(2):e0264040

    Article  Google Scholar 

  29. Rodréguez, SIR, de Carvalho FDAT (2019) A new fuzzy clustering algorithm for interval-valued data based on City-Block distance. 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), pp 1-6

  30. Vovan T, Phamgia T (2010) Clustering probability distributions. J Appl Stat 37(11):1891–1910

    Article  MathSciNet  Google Scholar 

  31. Vovan T, Nguyenthoi T, Voduy T, Hohuu V, Nguyentrang T (2017) Modified genetic algorithm-based clustering for probability density functions. J Stat Comput Simul 87(10):1964–1979

    Article  MathSciNet  Google Scholar 

  32. Vovan T (2017) L 1-distance and classification problem by bayesian method. J Appl Stat 44(3):385–401

    Article  MathSciNet  Google Scholar 

  33. Vovan T (2019) Cluster width of probability density functions. Intell Data Anal 23(2):385–405

    Article  MathSciNet  Google Scholar 

  34. Vovan T, NguyenTrang T (2018) Similar coefficient for cluster of probability density functions. Commun Stat - Theory Methods 47(8):1792–1811

    Article  MathSciNet  Google Scholar 

  35. Vovan T, Phamtoan D, Tranthituy D (2021) Automatic genetic algorithm in clustering for discrete elements. Commun Stat B: Simul 50(6):1679–1694

    Article  MathSciNet  Google Scholar 

  36. Vovan T, Phamtoan D, Tuan LH, Nguyentrang T (2021) An automatic clustering for interval data using the genetic algorithm. Ann Oper Res 303(1):359–380

    Article  MathSciNet  Google Scholar 

  37. Yaqoob I, Hashem IAT, Gani A, Mokhtar S, Ahmed E, Anuar NB, Vasilakos AV (2016) Big data: from beginning to future. Int J Inf Manag 36(6):1231–1247

  38. Xie XL, Beni GA (1991) Validity measure for fuzzy clustering. IEEE Trans Pattern Anal Mach Intell 13(8):841–847

    Article  Google Scholar 

Download references

Funding

This research is funded by Ministry of Education and Training in Viet Nam under Grant Number: B2022-TCT-03.

Author information

Authors and Affiliations

  1. Faculty of Mechanical - Electrical and Computer Engineering, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam

    Dinh Phamtoan

  2. College of Natural Science, Can Tho University, Can Tho City, Vietnam

    Tai Vovan

Authors
  1. Dinh Phamtoan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tai Vovan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tai Vovan.

Ethics declarations

Conflicts of interest

The authors declare that there is no conflict of interest with any financial organizations regarding the material reported in this manuscript.

Ethical approval

This study does not violate and does not involve moral and ethical statement.

Informed consent

The authors were aware of the publication of the paper and agreed to its publication.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Phamtoan, D., Vovan, T. Improving fuzzy clustering model for probability density functions using the two-objective genetic algorithm. Multimed Tools Appl 83, 45291–45314 (2024). https://doi.org/10.1007/s11042-023-17217-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-023-17217-5

Keywords

Search

Navigation