Skip to main content
Springer Nature Link
Log in

Image encryption algorithms based on two-dimensional discrete hyperchaotic systems and parallel compressive sensing

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

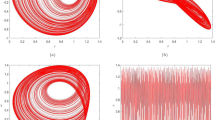
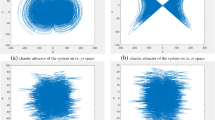
In this paper, a new two-dimensional discrete hyperchaotic system is proposed. Verification using the phase-track map, bifurcation map and Lyapunov exponent of the chaotic system shows that the chaotic system has better traversal, hyperchaos, unpredictability and wider chaotic region compared with the existing two-dimensional discrete chaotic systems. To improve the efficiency and security of the image encryption algorithm, this paper firstly uses parallel compressive sensing-aware image processing to greatly improve the efficiency of the image encryption. Secondly, index scrambling and forward and backward diffusion using a combination of a subset of discrete data sequences generated by a two-dimensional discrete hyperchaotic system improves the security of the image encryption algorithm. In addition ,the initial key and the sum of some pixel values of the original image are used to generate the initial values and control parameters of the 2D-SLS chaotic sequence using the hash of SHA-512, making the proposed algorithm robust to known plaintext and selected plaintext attacks. Simulation and experimental results show that the proposed algorithm is more efficient and secure than recently proposed encryption algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Algorithm 1
Fig. 4
Algorithm 2
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Data Availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Ajagbe SA, Adesina AO (2020) Design and development of an access control based electronic medical record (emr). CPJ 26:98–119

    Google Scholar 

  2. Liu JY, Yang DD, Zhou HB, Chen SQ (2018) A digital image encryption algorithm based on bit-planes and an improved logistic map. Multimed Tools Appl 77:10217–10233. https://doi.org/10.1007/s11042-017-5406-2

    Article  Google Scholar 

  3. Liu GZ,Wu Q,Wang GY,Jin PP (2022) A improved logistic chaotic map and its application to image encryption and hiding. J Electron Inf Technol 44:3602–3609. https://doi.org/10.11999/JEIT210763

  4. Li CL,Zhou Y,Li HM ,Feng W, Du JR (2021) Image encryption scheme with bit-level scrambling and multiplication diffusion. Multimed Tools Appl 80:18479 – 18501. https://doi.org/10.1007/s11042-021-10631-7

  5. Wu WS, Wang GY,Wu Q (2023) Image encryption based on improved two-dimensional mapping and dna coding. J Hangzhou Dianzi Univ (Nat Sci) 43:34–4048

  6. Deng WB, Liu S, Liu FC, Huang RN (2022) An image encryption algorithm based on compressed sensing and DNA coding. Comput Eng Sci 44(9):1574–1582

    Google Scholar 

  7. Wu XG,Wang KS,Wang XY, KanHB, Jürgen Kurths (2018) Color image dna encryption using nca map-based cml and one-time keys. Signal Proc 148(jul.):272–287. https://doi.org/10.1016/j.sigpro.2018.02.028

  8. Dong WL, Li QL, Tang YW, Hu M, Zeng R (2021) A robust and multi chaotic DNA image encryption with pixel-value pseudorandom substitution scheme. Opt Commun 499(127):211. https://doi.org/10.1016/j.optcom.2021.127211

    Article  Google Scholar 

  9. Yousif SF, Abboud AJ, Alhumaima RS (2022) A new image encryption based on bit replacing, chaos and DNA coding techniques. Multimedia Tools Appl 81:27453–27493. https://doi.org/10.1007/s11042-022-12762-x

    Article  Google Scholar 

  10. Brahim Anis Bacha Bel Hadj, NHs Adda Ali Pacha, (2023) A new image compression-encryption scheme based on compressive sensing & classical AES algorithm. Multimed Tools Appl 1–31. https://doi.org/10.1007/s11042-023-15171-w

  11. Hafsa A, Sghaier A, Malek J, Machhout M (2021) Image encryption method based on improved ecc and modified AES algorithm. Multimed Tools Appl 80:19769–19801. https://doi.org/10.1007/s11042-021-10700-x

    Article  Google Scholar 

  12. Sun FY, Lv ZB (2021) A secure image encryption based on spatial surface chaotic system and AES algorithm. Multimed Tools Appl 81:3959–3979. https://doi.org/10.1007/s11042-021-11690-6

    Article  Google Scholar 

  13. Jiang DH, Zhu LY, Shen ZY, Wang XY, Chen YP (2022) A double image visual security encryption algorithm combining 2d compressive sensing and chaotic mapping. J Xi’an Jiaotong Univ 56(002):140–148

    Google Scholar 

  14. Wang XY, Liu C, Jiang DH (2021) A novel triple-image encryption and hiding algorithm based on chaos, compressive sensing and 3d DCT. Inf Sci 574:505–527. https://doi.org/10.1016/j.ins.2021.06.032

    Article  MathSciNet  Google Scholar 

  15. Hua ZY, Zhou YC, Huang HJ (2019) Cosine-transform-based chaotic system for image encryption. Inf Sci Int J 480:403–419. https://doi.org/10.1016/j.ins.2018.12.048

    Article  Google Scholar 

  16. Mansouri Ali, Wang XY (2020) A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme. Inf Sci 520:46–62. https://doi.org/10.1016/j.ins.2020.02.008

    Article  MathSciNet  Google Scholar 

  17. Tang ZJ, Yang Y, Xu SJ, Yu CQ, Zhang XQ et al (2019) Image encryption with double spiral scans and chaotic maps. Secur Commun Netw 2019. https://doi.org/10.1155/2019/8694678

  18. Tang ZJ, Wang F, Zhang XQ (2017) Image encryption based on random projection partition and chaotic system. Multimed Tools Appl 76:8257–8283. https://doi.org/10.1007/s11042-016-3476-1

    Article  Google Scholar 

  19. Hua ZY, Zhou YC (2016) Image encryption using 2d logistic-adjusted-sine map. Inf Sci 339:237–253. https://doi.org/10.1016/j.ins.2016.01.017

    Article  Google Scholar 

  20. Liu SC ,Li CB,Li YX (2022) A novel image encryption algorithm based on exponent-cosine chaotic mapping. J Electron Inf Technol 44(5):1754–1762. https://doi.org/10.11999/JEIT210270

  21. Chen S, Lü J, (2002) Parameters identification and synchronization of chaotic systems based upon adaptive control. Phys Lett A 299(4):353–358. https://doi.org/10.1016/S0375-9601(02)00522-4

  22. Ye GD (2010) Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recogn Lett 31(5):347–354. https://doi.org/10.1016/j.patrec.2009.11.008

    Article  Google Scholar 

  23. Donoho D (2006) Compressed sensing. IEEE Trans Inf Theory 52(4):1289–1306. https://doi.org/10.1109/TIT.2006.871582

    Article  Google Scholar 

  24. Shi H, Wang LD (2019) Multi-process image encryption scheme based on compressed sensing and multi-dimensional chaotic system*. Acta PhysSin 68(20):39–52. https://doi.org/10.7498/aps.68.20190553

    Article  Google Scholar 

  25. Gong LH, Qiu KD, Deng CW, Zhou NR (2019) An image compression and encryption algorithm based on chaotic system and compressive sensing. Opt Laser Technol 115:257–267. https://doi.org/10.1016/j.optlastec.2019.01.039

    Article  Google Scholar 

  26. Hua ZY, Zhang KY, Li YM, Zhou YC (2021) Visually secure image encryption using adaptive-thresholding sparsification and parallel compressive sensing. Signal Process 183(107):998. https://doi.org/10.1016/j.sigpro.2021.107998

    Article  Google Scholar 

  27. HY W, Vieira J (2010) 2-d wavelet transforms in the form of matrices and application in compressed sensing. 2010 8th World Congress on Intelligent Control and Automation

  28. Fay R, Ruland C (2016) Compressive sensing encryption modes and their security. 2016 11th International Conference for Internet Technology and Secured Transactions (ICITST)

  29. Cai J, Xie SC, Zhang JZ (2023) Image compression-encryption algorithm based on chaos and compressive sensing. Multimed Tools Appl 82(14):22189–22212. https://doi.org/10.1007/s11042-022-13346-5

    Article  Google Scholar 

  30. Wang ZP, Jiang YN, Chen SF (2022) Image parallel block compressive sensing scheme using DFT measurement matrix. Multimed Tools Appl 82:21561–21583. https://doi.org/10.1007/s11042-022-14176-1

    Article  Google Scholar 

  31. Sun KH (2015) Principle and technology of chaotic secure communication. Tsinghua University Press, BeiJing

    Google Scholar 

  32. Candes EJ, Tao T (2005) Decoding by linear programming. IEEE Trans Inf Theory 51(12):4203–4215. https://doi.org/10.1109/TIT.2005.858979

    Article  MathSciNet  Google Scholar 

  33. Pati Y, Rezaiifar R, Krishnaprasad P (1993) Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. In: Proceedings of 27th Asilomar Conference on Signals, Systems and Computers

  34. Dai W, Milenkovic O (2008) Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans Inf Theory 55(5):2230–2249. https://doi.org/10.1109/TIT.2009.2016006

    Article  MathSciNet  Google Scholar 

  35. Mohimani GH, Babaie-Zadeh M, Jutten C (2007) Fast sparse representation based on smoothed 0 norm. In: International Conference on Independent Component Analysis & Signal Separation, pp 389–396

  36. Alvarez G, Li S (2006) Some basic cryptographic requirements for chaos-based cryptosystems. Int J Bifurcation Chaos Appl Sci Eng 16:2129–2151. https://doi.org/10.1142/S0218127406015970

    Article  MathSciNet  Google Scholar 

  37. Wei DYJM (2021) A fast image encryption algorithm based on parallel compressive sensing and DNA sequence. Opt - Int J Light Electron Opt 238(6):166748. https://doi.org/10.1016/j.ijleo.2021.166748

  38. Musanna F, Kumar S (2020) A novel image encryption algorithm using chaotic compressive sensing and nonlinear exponential function. J Inf Secur Appl 54:102560. https://doi.org/10.1016/j.jisa.2020.102560

    Article  Google Scholar 

  39. Zhou KL, Fan JJ, Fan HJ, Li M (2020) Secure image encryption scheme using double random-phase encoding and compressed sensing. Opt Laser Technol 121:105769–105769. https://doi.org/10.1016/j.optlastec.2019.105769

    Article  Google Scholar 

  40. Xu QY, Sun KH, He SB, Zhu CX (2020) An effective image encryption algorithm based on compressive sensing and 2d-slim. Opt Lasers Eng 134:106178. https://doi.org/10.1016/j.optlaseng.2020.106178

    Article  Google Scholar 

  41. Liu JL, Zhang M, Tong X, Wang Z (2021) Image compression and encryption algorithm based on compressive sensing and nonlinear diffusion. Multimed Tools Appl 80(17):25433–25452. https://doi.org/10.1007/s11042-021-10884-2

    Article  Google Scholar 

  42. Liang F, Li Y, Chen CH, Ye ZY, Zhou JT (2017) Ossim:an object-based multiview stereo algorithm using ssim index matching cost. IEEE Trans Geoence Remote Sens 55(12):6937–6949. https://doi.org/10.1109/TGRS.2017.2737033

    Article  Google Scholar 

  43. Xu J, Mou J, Liu J, Hao J (2022) The image compression-encryption algorithm based on the compression sensing and fractional-order chaotic system. Vis Comput 38:1509–1526. https://doi.org/10.1007/s00371-021-02085-7

    Article  Google Scholar 

  44. Gan ZH, Chai XL, Zhang JT, Zhang YS, Chen YR (2020) An effective image compression-encryption scheme based on compressive sensing (CS) and game of life (gol). Neural Comput & Applic 32:14113–14141. https://doi.org/10.1007/s00521-020-04808-8

    Article  Google Scholar 

  45. Xu QY, Sun KH, He SB, Zhu CX (2020) An effective image encryption algorithm based on compressive sensing and 2d-slim. Optics Lasers Eng 134(106):178. https://doi.org/10.1016/j.optlaseng.2020.106178

    Article  Google Scholar 

  46. Chai XL, Zheng XY, Gan ZH, Han DJ, Chen YR (2018) An image encryption algorithm based on chaotic system and compressive sensing. Signal Process 148:124–144. https://doi.org/10.1016/j.sigpro.2018.02.007

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Hubei Minzu University, Enshi 445000, Hubei, China

    Yuhui Gao

  2. College of Intelligent Systems Science and Engineering, Hubei Minzu University, Enshi 445000, Hubei, China

    Jingyi Liu & Shiqiang Chen

Authors
  1. Yuhui Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jingyi Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shiqiang Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Shiqiang Chen.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, Y., Liu, J. & Chen, S. Image encryption algorithms based on two-dimensional discrete hyperchaotic systems and parallel compressive sensing. Multimed Tools Appl 83, 57139–57161 (2024). https://doi.org/10.1007/s11042-023-17745-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-023-17745-0

Keywords