Skip to main content
Springer Nature Link
Log in

Lightweight encryption scheme based on a new NLFSR

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

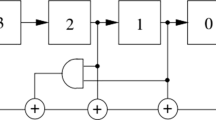
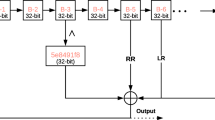
This paper presents a new nonlinear feedback shift register (NLFSR) in the Galois configuration to generate the pseudorandom number sequences (PRNS) for a lightweight encryption scheme. In the NLFSR, the feedback function is applied to each state, not only the last bit of NLFSR. In the proposed design the size of the feedback is reduced using Galois configuration. The NLFSR is tested with NIST Statistical Test Suite to evaluate its quality randomness. The new NLFSR is used as an pseudorandom number generator to design a new lightweight image encryption algorithm. The encryption process can be represent in two phases permutation and diffusion. In the first phase, two different PRNSs generated by the new NLFSR for permute the row and column pixels of the plain image (PI). Then convert the permuted image into a 1D binary vector. In the diffusion phase, DNA arithmetic is applied between the 1D and another PRNS generated by the same NLFSR with different key. Several security analysis tests are performed on the proposed scheme (like histogram analysis, entropy, correlation coefficient, NPCR, UACI, MSE, and PSNR ) to test the security strength of the encryption method. It was found that the new NLFSR had passes all the tests in NIST Statistical Test Suite, and the test results of the encryption scheme are also acceptable and shows potential security strength.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Algorithm 1
Algorithm 2
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Adhikari S, Karforma S (2021) A novel image encryption method for e-governance application using elliptic curve pseudo random number and chaotic random number sequence. Multimed Tools Appl 1–26

  2. Ali TS, Ali R (2020) A new chaos based color image encryption algorithm using permutation substitution and boolean operation. Multimed Tools Appl 79(27):19853–19873

    Article  Google Scholar 

  3. Dey S, Sarkar S (2021) A theoretical investigation on the distinguishers of salsa and chacha. Discret Appl Math 302:147–162

    Article  MathSciNet  Google Scholar 

  4. Dubrova E, Hell M (2017) Espresso: A stream cipher for 5g wireless communication systems. Cryptogr Commun 9(2):273–289

    Article  MathSciNet  Google Scholar 

  5. Erkan U, Toktas A, Toktas F, Alenezi F (2022) 2d e\(\pi \)-map for image encryption. Inf Sci 589:770–789

    Article  Google Scholar 

  6. Fu J, Gan Z, Chai X, Lu Y (2022) Cloud-decryption-assisted image compression and encryption based on compressed sensing. Multimed Tools Appl 81(12):17401–17436

    Article  Google Scholar 

  7. Hamann M, Krause M, Meier W (2017) Lizard-a lightweight stream cipher for power-constrained devices. IACR Trans Symmetric Cryptol 2017(1):45–79

    Article  Google Scholar 

  8. Hamann M, Krause M, Meier W, Zhang B (2018) Design and analysis of small-state grain-like stream ciphers. Cryptogr Commun 10(5):803–834

    Article  MathSciNet  Google Scholar 

  9. Hell M, Johansson T, Maximov A, Meier W (2008) The grain family of stream ciphers. In: New Stream Cipher Designs, pp 179–190. Springer

  10. Hua Z, Li J, Li Y, Chen Y (2021) Image encryption using value-differencing transformation and modified zigzag transformation. Nonlinear Dyn 106:3583–3599

    Article  Google Scholar 

  11. Jiang Y (2020) Weak grain-like structures. IEEE Trans Inf Theory 66(12):7717–7723

    Article  MathSciNet  Google Scholar 

  12. Kumari P, Mondal B (2023) An encryption scheme based on grain stream cipher and chaos for privacy protection of image data on iot network. Wirel Pers Commun 130(3):2261–2280

    Article  Google Scholar 

  13. Kumari P, Mondal B (2023) Lightweight image encryption algorithm using nlfsr and cbc mode. J Supercomput 130:1–21

    Google Scholar 

  14. Li B, Liu M, Lin D (2020) Fpga implementations of grain v1, mickey 2.0, trivium, lizard and plantlet. Microprocess Microsyst 78:103210

    Article  Google Scholar 

  15. Li F, Wu H, Zhou G, Wei W (2019) Robust real-time image encryption with aperiodic chaotic map and random-cycling bit shift. J Real Time Image Process 16(3):775–790

    Article  Google Scholar 

  16. Lyle M, Sarosh P, Parah SA (2022) Adaptive image encryption based on twin chaotic maps. Multimed Tools Appl 81(6):8179–8198

    Article  Google Scholar 

  17. Ahmad ZUSKFAM, Alam MZ (2018) An image encryption approach using particle swarm optimization and chaotic map. Int J Inf Technol 10(3):247–255

    Google Scholar 

  18. McKay K (2016) Users guide to running the draft nist sp 800–90b entropy estimation suite. Tech. Rep. SP, NIST, Gaithersburg, MD, USA

    Google Scholar 

  19. Mondal B (2018) Cryptographic image scrambling techniques. In: J Inf Secur Cryptogr, pages 37–65. CRC Press

  20. Naskar PK, Bhattacharyya S, Mahatab KC, Dhal KG, Chaudhuri A (2021) An efficient block-level image encryption scheme based on multi-chaotic maps with dna encoding. Nonliner Dyn 105(4):3673–3698

    Article  Google Scholar 

  21. Pourjabbar Kari A, Habibizad Navin A, Bidgoli AM, Mirnia M (2021) A new image encryption scheme based on hybrid chaotic maps. Multimed Tools Appl 80:2753–2772

    Article  Google Scholar 

  22. Praveenkumar P, Amirtharajan R, Thenmozhi K, Rayappan JBB (2017) Fusion of confusion and diffusion: a novel image encryption approach. Telecommun Syst 65(1):65–78

    Article  Google Scholar 

  23. Ruk A et al (2001) A statistical test suite for the validation of random number generators and pseudo-random number generators for cryptographic applications. NIST. http://csrc.nist.gov/rng/rng2.html

  24. Rukhin A, Soto J, Nechvatal J, Smid M, Barker E, Leigh S, Levenson M, Vangel M, Banks D, Heckert A et al (2001) A statistical test suite for random and pseudorandom number generators for cryptographic applications, vol. 22. US Department of Commerce, Technology Administration, National Institute of \(\ldots \)

  25. Shah AA, Parah SA, Rashid M, Elhoseny M (2020) Efficient image encryption scheme based on generalized logistic map for real time image processing. J Real Time Image Process 17(6):2139–2151

    Article  Google Scholar 

  26. Shahna K (2023) Novel chaos based cryptosystem using four-dimensional hyper chaotic map with efficient permutation and substitution techniques. Chaos Solit Fractals 170:113383

    Article  MathSciNet  Google Scholar 

  27. Shahna K, Mohamed A (2021) Novel hyper chaotic color image encryption based on pixel and bit level scrambling with diffusion. Signal Process Image Commun 99:116495

    Article  Google Scholar 

  28. Shi Z, Jin C, Zhang J, Cui T, Ding L, Jin Y (2023) A general correlation evaluation model on lfsr-based stream ciphers. IEEE Trans Inf Theory 69(10):6682–6699

    Article  MathSciNet  Google Scholar 

  29. Suresh T, Ramakrishnan M (2020) Design of low power nfsr for rfid system with irregular clock pulse. Microprocess Microsyst 73:102983

    Article  Google Scholar 

  30. Tiwari D, Mondal B, Singh SK, Koundal D (2023) Lightweight encryption for privacy protection of data transmission in cyber physical systems. Clust Comput 26(4):2351–2365

    Article  Google Scholar 

  31. Toktas A, Erkan U, Ustun D (2021) An image encryption scheme based on an optimal chaotic map derived by multi-objective optimization using abc algorithm. Nonlinear Dyn 105(2):1885–1909

    Article  Google Scholar 

  32. Wang T, Wang MH (2020) Hyperchaotic image encryption algorithm based on bit-level permutation and DNA encoding. Opt Laser Technol 132:106355

    Article  Google Scholar 

  33. Wei D, Jiang M, Deng Y (2023) A secure image encryption algorithm based on hyper-chaotic and bit-level permutation. Expert Syst Appl 213:119074

    Article  Google Scholar 

  34. Xu C, Sun J, Wang C (2020) A novel image encryption algorithm based on bit-plane matrix rotation and hyper chaotic systems. Multimed Tools Appl 79(9–10):5573–5593

    Article  Google Scholar 

  35. Yao G, Parampalli U (2022) Improved transformation algorithms for generalized galois nlfsrs. Cryptogr Commun 14(2):229–258

    Article  MathSciNet  Google Scholar 

  36. Zhang D, Wen X, Yan C, Li T (2023) An image encryption algorithm based on joint rna-level permutation and substitution. Multimed Tools Appl 82(15):23401–23426

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science and Engineering, National Institute of Technology Patna, Patna, 800005, India

    Punam Kumari & Bhaskar Mondal

Authors
  1. Punam Kumari
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Bhaskar Mondal
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Bhaskar Mondal.

Ethics declarations

The authors hereby declare that there was no full or partial financial support from any organization. The author do not have any Conflicts of interest to disclosures.    Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumari, P., Mondal, B. Lightweight encryption scheme based on a new NLFSR. Multimed Tools Appl 83, 64919–64943 (2024). https://doi.org/10.1007/s11042-024-18222-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-024-18222-y

Keywords