Skip to main content

Advertisement

Springer Nature Link
Log in

Holographic encryption algorithm based on DNA coding and bit-plane decomposition

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

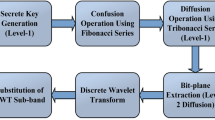
In recent years, encryption algorithms have undergone rapid development, finding extensive applications across diverse industries. In the pursuit of enhancing the security of image encryption methodologies, this paper introduces a novel computational holographic encryption approach grounded in DNA coding and bit-plane decomposition. The encryption framework employs a Logistic-Sine chaotic mapping system characterized by a substantial key space to control encryption particulars. The plaintext image undergoes encryption through the input–output algorithm of computational holography. This algorithm shifts information from the spatial domain, represented by the greyscale map, to the frequency domain, concealing the distribution of pixel values. The incorporation of DNA coding and bit-plane transformations serves to intensify the chaos within the ciphertext image, thereby maximizing the efficacy of the encryption process. By integrating principles from biology and physical optics into encryption methodologies, this approach amalgamates diverse scientific domains. Simulation results and data analyses substantiate that the proposed encryption algorithm adeptly withstands various attacks, attesting to its security and reliability.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data availability

Lena is available at http://www.lenna.org/. Baboon, peppers and goldhill are available at https://sipi.usc.edu/database/. The encryption and decryption algorithms proposed in the paper can be accessed in https://github.com/legend-liang/Holographic-encryption-algorithm-based-on-DNA-coding-and-bit-plane-decomposition.git.

Abbreviations

Ambut:

Full Name

DNA:

DeoxyriboNucleic Acid

DES:

Data Encryption Standard

RSA:

Rivest-Shamir-Adleman

FFT:

Fast Fourier transform

IFFT:

Inverse Fast Fourier transform

GS:

Gerchberg-Saxton

XOR:

Exclusive OR

CPU:

Central Processing Unit

NPCR:

Number of Pixels Changed Rate

UACI:

Unified Average Change Intensity

PSNR:

Peak Signal-to-Noise Ratios

RGB:

Red-Green–Blue

References

  1. Zhang X et al (2014) Compressing encrypted images with auxiliary information. IEEE Trans Multimed 16(5):1327–1336

    Google Scholar 

  2. Ke Y et al (2020) Fully homomorphic encryption encapsulated difference expansion for reversible data hiding in encrypted domain. IEEE Trans Circuits Syst Video Technol 30(8):2353–2365

    Google Scholar 

  3. Yu C et al (2021) Reversible data hiding with hierarchical embedding for encrypted images. IEEE Transact Circuits Syst Video Technol 32(2):451–466

    Google Scholar 

  4. Du Y, Yin Z, Zhang X (2020) High capacity lossless data hiding in JPEG bitstream based on general VLC mapping. IEEE Trans Dependable Secure Comput 19(2):1420–1433

    Google Scholar 

  5. Li S, Ma R, Zhang H (2019) Enhancing security for JPEG Image against mosaic attack using Inter-block shuffle encryption. IEEE Access 7:72696–72702

    Google Scholar 

  6. Wu Y, Dai X (2020) Encryption of accounting data using DES algorithm in computing environment. J Intell Fuzzy Syst 39(4):5085–5095

    Google Scholar 

  7. Shao Z, Gao Y (2015) Certificate-based verifiably encrypted RSA signatures. Trans Emerg Telecommun Technol 26(2):276–289

    Google Scholar 

  8. Li S et al (2006) Chaos-based encryption for digital image and video. In: Furht B, Kirovski D (eds) Multimedia encryption and authentication techniques and applications. Auerbach Publications, pp 129–163. https://doi.org/10.1201/9781420013450-4

  9. Mazloom S, Eftekhari-Moghadam AM (2009) Color image encryption based on coupled nonlinear chaotic map. Chaos Solitons Fractals 42(3):1745–1754

    Google Scholar 

  10. Nithya R, Dhanasekaran D (2022) Novel dominant color subband image encryption in visual sensor network for smart military surveillance system. Traitement Du Signal 39(3):951–960. https://doi.org/10.18280/ts.390322

  11. Alslman Y et al (2022) Hybrid encryption scheme for medical imaging using autoencoder and advanced encryption standard. Electronics 11(23):3967

    Google Scholar 

  12. Deb S, Biswas B, Bhuyan B (2019) Secure image encryption scheme using high efficiency word-oriented feedback shift register over finite field. Multimed Tools Appl 78:34901–34925

    Google Scholar 

  13. Zope-Chaudhari S, Venkatachalam P, Buddhiraju KM (2015) Secure dissemination and protection of multispectral images using crypto-watermarking. IEEE J Select Top Appl Earth Obs Remote Sensing 8(11):5388–5394

    Google Scholar 

  14. Song C, Qiao Y (2015) A novel image encryption algorithm based on DNA encoding and spatiotemporal chaos. Entropy 17(10):6954–6968

    MathSciNet  Google Scholar 

  15. Matthews R (1989) On the derivation of a “chaotic” encryption algorithm. Cryptologia 13(1):29–42

    MathSciNet  Google Scholar 

  16. Chai X et al (2020) Color image compression and encryption scheme based on compressive sensing and double random encryption strategy. Signal Process 176:107684

    Google Scholar 

  17. Chen C, Sun K, He S (2020) An improved image encryption algorithm with finite computing precision. Signal Process 168:107340

    Google Scholar 

  18. Hou W et al (2020) A novel image-encryption scheme based on a non-linear cross-coupled hyperchaotic system with the dynamic correlation of plaintext pixels. Entropy 22(7):779

    MathSciNet  Google Scholar 

  19. Çelik H, Doğan N (2023) A hybrid color image encryption method based on extended logistic map. Multimed Tools Appl 83(5):12627–12650. https://doi.org/10.1007/s11042-023-16215-x

  20. Iqbal N et al (2023) An efficient image cipher based on the 1D scrambled image and 2D logistic chaotic map. Multimed Tools Appl 82(26):40345–40373. https://doi.org/10.1007/s11042-023-15037-1

  21. Hazer A, Yıldırım R (2021) A review of single and multiple optical image encryption techniques. J Opt 23(11):113501

    Google Scholar 

  22. Liu S, Guo C, Sheridan JT (2014) A review of optical image encryption techniques. Opt Laser Technol 57:327–342

    Google Scholar 

  23. Chen W, Javidi B, Chen X (2014) Advances in optical security systems. Adv Opt Photon 6(2):120–155

    Google Scholar 

  24. Refregier P, Javidi B (1995) Optical image encryption based on input plane and Fourier plane random encoding. Opt Lett 20(7):767–769

    Google Scholar 

  25. Qin W, Peng X (2010) Asymmetric cryptosystem based on phase-truncated Fourier transforms. Opt Lett 35(2):118–120

    Google Scholar 

  26. Clemente P et al (2010) Optical encryption based on computational ghost imaging. Opt Lett 35(14):2391–2393

    Google Scholar 

  27. Tsang PWM (2017) Single-random-phase holographic encryption of images. Opt Lasers Eng 89:22–28

    Google Scholar 

  28. Piao M-L et al (2019) Robust multidepth object encryption based on a computer-generated hologram with a cascaded structure. Appl Opt 58(36):9921–9930

    Google Scholar 

  29. Kong D et al (2017) Image encryption based on interleaved computer-generated holograms. IEEE Trans Indust Inform 14(2):673–678

    Google Scholar 

  30. Wang X, Zhao D (2012) Fully phase multiple-image encryption based on superposition principle and the digital holographic technique. Opt Commun 285(21–22):4280–4284

    Google Scholar 

  31. Abookasis D, Rosen J (2006) Three types of computer-generated hologram synthesized from multiple angular viewpoints of a three-dimensional scene. Appl Opt 45(25):6533–6538

    Google Scholar 

  32. Tricoles G (1987) Computer generated holograms: an historical review. Appl Opt 26(20):4351–4360

    Google Scholar 

  33. Zhou P et al (2019) Dynamic compensatory Gerchberg-Saxton algorithm for multiple-plane reconstruction in holographic displays. Opt Express 27(6):8958–8967

    Google Scholar 

  34. Yifat Y et al (2014) Highly efficient and broadband wide-angle holography using patch-dipole nanoantenna reflectarrays. Nano Lett 14(5):2485–2490

    Google Scholar 

  35. Sun S et al (2012) Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater 11(5):426–431

    Google Scholar 

  36. Liu L et al (2014) Broadband metasurfaces with simultaneous control of phase and amplitude. Adv Mater 26(29):5031–5036

    Google Scholar 

  37. Chong KE et al (2016) Efficient polarization-insensitive complex wavefront control using Huygens’ metasurfaces based on dielectric resonant meta-atoms. Acs Photon 3(4):514–519

    Google Scholar 

  38. Zhao W et al (2016) Dielectric Huygens’ metasurface for high-efficiency hologram operating in transmission mode. Sci Reports 6(1):30613

    Google Scholar 

  39. Chen WT et al (2014) High-efficiency broadband meta-hologram with polarization-controlled dual images. Nano Lett 14(1):225–230

    Google Scholar 

  40. Montelongo Y et al (2014) Polarization switchable diffraction based on subwavelength plasmonic nanoantennas. Nano Lett 14(1):294–298

    MathSciNet  Google Scholar 

  41. Zhu M, Wang C (2020) A novel parallel chaotic system with greatly improved Lyapunov exponent and chaotic range. Int J Mod Phys B 34(07):2050048

    MathSciNet  Google Scholar 

  42. Qi G, Chen G (2015) A spherical chaotic system. Nonlinear Dyn 81:1381–1392

    MathSciNet  Google Scholar 

  43. Li Q, Chen L (2023) An image encryption algorithm based on 6-dimensional hyper chaotic system and DNA encoding. Multimed Tools Appl 83(2):5351–5368. https://doi.org/10.1007/s11042-023-15550-3

  44. Wang Y et al (2015) Security analysis on a color image encryption based on DNA encoding and chaos map. Comput Electr Eng 46:433–446

    Google Scholar 

  45. Zhou Y et al (2012) Image encryption using P-Fibonacci transform and decomposition. Opt Commun 285(5):594–608

    Google Scholar 

  46. Alvarez G, Li S (2006) Some basic cryptographic requirements for chaos-based cryptosystems. Int J Bifurcation Chaos 16(08):2129–2151

    MathSciNet  Google Scholar 

  47. Li J et al (2022) Holographic encryption algorithm based on bit-plane decomposition and hyperchaotic Lorenz system. Opt Laser Technol 152:108127

    Google Scholar 

  48. Wan Y, Wang S, Baoxiang Du (2023) A bit plane image encryption algorithm based on compound chaos. Multimed Tools Appl 82(14):22103–22121

    Google Scholar 

  49. Musanna F, Kumar S (2020) Image encryption using quantum 3-D Baker map and generalized gray code coupled with fractional Chen’s chaotic system. Quantum Inf Process 19:1–31

    MathSciNet  Google Scholar 

  50. Tian J et al (2021) A novel image encryption algorithm using PWLCM map-based CML chaotic system and dynamic DNA encryption. Multimed Tools Appl 80(21–23):32841–32861

    Google Scholar 

Download references

Acknowledgements

This research is supported by the National Natural Science Foundation of China under Grants No. 62175039.

Author information

Authors and Affiliations

  1. School of Physics and Opto-Electronic Engineering, Guangdong University of Technology, Guangzhou, 510006, China

    Zheng Liang, Li Chen, Kai Chen, Zhenhui Liang, Kunhua Wen & Yihua Hu

  2. Guangdong Provincial Key Laboratory of Information Photonics Technology, Guangdong University of Technology, Guangzhou, China

    Li Chen

  3. Zhongshan Zhongying Optical Co., Zhongshan, 528441, Guangdong, China

    Jiawei Zhu

Authors
  1. Zheng Liang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Li Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Kai Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Zhenhui Liang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Kunhua Wen
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Jiawei Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

  7. Yihua Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Li Chen.

Ethics declarations

Competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Fig. 10
figure 10

The general model of the hologram

Full size image
Fig. 11
figure 11

Schematic diagram of the GS algorithm

Full size image
Fig. 12
figure 12

Comparison of Lyapunov indices

Full size image
Fig. 13
figure 13

The Lyapunov index of Logistic-sine chaotic system

Full size image
Fig. 14
figure 14

The scatterplot of Logistic-sine chaotic system

Full size image

Tables 8, 9, 10, 11 and 12.

Table 8 DNA addition
Full size table
Table 9 DNA subtraction
Full size table
Table 10 DNA XOR computing
Full size table
Table 11 DNA XNOR computing
Full size table
Table 12 Reordering rules
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liang, Z., Chen, L., Chen, K. et al. Holographic encryption algorithm based on DNA coding and bit-plane decomposition. Multimed Tools Appl 83, 87385–87413 (2024). https://doi.org/10.1007/s11042-024-18838-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-024-18838-0

Keywords