Skip to main content

Advertisement

Springer Nature Link
Log in

High-resolution estimation of the directions-of-arrival distribution by algebraic phase unwrapping algorithms

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

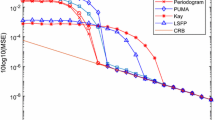
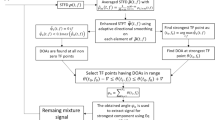
Abstract

We present nontrivial utilization methods of a pair of symbolic algebraic algorithms (Yamada et al. in IEEE Trans Signal Process 46:1639–1664, 1998; Yamada and Bose in IEEE Trans Circuits Syst 1 Fundam Theory Appl 49:298–304, 2002) which were developed originally for multidimensional phase unwrapping and zero-distribution problems. Given the minor subspace of the covariance matrix of the data measured at a uniform linear array of sensors, the proposed methods provide estimates of the Directions-of-Arrival (DOA) distribution of multiple narrowband signals, i.e., the number of DOA in an arbitrarily specified range, without using any numerical search for each direction of arrival. The proposed methods can serve as powerful mathematical tools to extract global information in the high-resolution DOA estimation problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Barabell, A. J. (1983, May). Improving the resolution performance of eigenstructure-based direction-finding algorithms. In Proceedings of IEEE ICASSP’83 (pp. 336–339).

  • Belloni F., Richter A., Koivunen V. (2007) DoA estimation via manifold separation for arbitrary array structures. IEEE Transactions on Signal Processing 55(10): 4800–4810

    Article  MathSciNet  Google Scholar 

  • Bienvenu, G. (1979, May). Influence of the spatial coherence of the background noise on high resolution passive methods. In Proceedings of IEEE ICASSP’79 (pp. 306–309).

  • Chen J. C., Yao K., Hudson R. E. (2002) Source localization and beamforming. IEEE Signal Processing Magazine 19: 30–39

    Article  Google Scholar 

  • Friedlander B. (1993) The root-MUSIC algorithm for direction finding with interpolated arrays. Signal Processing 30: 15–29

    Article  MATH  Google Scholar 

  • Godara L. C. (1997a) Application of antenna arrays to mobile communications, Part I: Performance improvement, feasibility, and system considerations. Proceedings of the IEEE 85: 1031–1050

    Article  Google Scholar 

  • Godara L. C. (1997b) Application of antenna arrays to mobile communications, Part II: Beam-forming and direction-of-arrival considerations. Proceedings of the IEEE 85: 1195–1245

    Article  Google Scholar 

  • Godara L. C. (2004) Smart antennas. CRC Press, Boca Raton

    Book  Google Scholar 

  • Henrici P. (1974) Applied and computational complex analysis. Wiley, New York

    MATH  Google Scholar 

  • Hyberg P., Jansson M., Ottersten B. (2004) Array interpolation and bias reduction. IEEE Transactions on Signal Processing 52(10): 2711–2720

    Article  Google Scholar 

  • Hyberg P., Jansson M., Ottersten B. (2005) Array interpolation and DOA MSE reduction. IEEE Transactions on Signal Processing 53(12): 4464–4471

    Article  MathSciNet  Google Scholar 

  • Ichige, K., Imai, M., Arai, H., Nakano, M., & Hirano M. (2006, May). Direction of arrival detection system for radio surveillance: Frequency spectrum analysis of CDMA and jamming waves. In Proceedings of the IEEE vehicular technology conference (VTC-spring), no. 11H-1, Melbourne, Australia.

  • Mathews C. P., Zoltowski M. D. (1994) Eigenstructure techniques for 2-D angle estimation with uniform circular arrays. IEEE Transactions on Signal Processing 42(9): 2395–2407

    Article  Google Scholar 

  • Misono M., Yamada I. (2008) An efficient adaptive minor subspace extraction using exact nested orthogonal complement structure. IEICE Transactions on Fundamentals of Electronics 91-A(8): 1867–1874

    Article  Google Scholar 

  • Ouyang S., Bao Z., Liao G.-S., Ching P. C. (2001) Adaptive minor component extraction with modular structure. IEEE Transactions on Signal Processing 49: 2127–2137

    Article  Google Scholar 

  • Rao B. D., Hari K. V. S. (1989) Performance analysis of Root-MUSIC. IEEE Transactions on Acoustics, Speech and Signal Processing 37: 1939–1949

    Article  Google Scholar 

  • Rapapport, T. S. (eds) (1998) Smart antennas: Adaptive arrays, algorithms, and wireless position location. IEEE Press, Piscataway, NJ

    Google Scholar 

  • Roy R., Kailath T. (1989) ESPRIT—Estimation of signal parameter via rotational invariance techniques. IEEE Transactions on Acoustics, Speech and Signal Processing 37: 984–995

    Article  Google Scholar 

  • Schmidt, R. O. (1979) Multiple emitter location and signal parameter estimation. In Proceedings of RADC, spectral estimation workshop (pp. 243–258) Rome, NY.

  • Shirayanagi, K., & Sweedler, M. (1995). A theory of stabilizing algebraic algorithms (pp. 1–92). Technical Report 95-28, Mathematical Sciences Institute, Cornell University.

  • Shirayanagi K., Sekigawa H. (1997) An interval method based on zero rewriting and its application to Sturm’s algorithm. IEICE Transactions on Fundamentals (Japanese Edition) 80-A: 791–801

    Google Scholar 

  • Sidrovich D. V., Gershman A. B. (1998) Two-dimensional wideband interpolated root-MUSIC applied to measured seismic data. IEEE Transactions on Signal Processing 46: 2263–2267

    Article  Google Scholar 

  • Stoica P., Moses R. (1997) Introduction to spectral analysis. Prentice-Hall, New Jersey

    MATH  Google Scholar 

  • Van Trees H. L. (2002) Optimum array processing. Wiley, New York

    Book  Google Scholar 

  • Wang H., Kaveh M. (1985) Coherent signal-subspace processing for detection and estimation of angles of arrival of multiple wide-band sources. IEEE Transactions on Acoustics, Speech and Signal Processing 33: 823–831

    Article  Google Scholar 

  • Wax M., Kailath T. (1985) Detection of signals by information theoretic criteria. IEEE Transactions on Acoustics, Speech and Signal Processing 33: 387–392

    Article  MathSciNet  Google Scholar 

  • Weiss A. J., Friedlander B. (1993) Range and bearing estimation using polynomial rooting. IEEE Journal on Oceanic Engineering 18: 130–137

    Article  Google Scholar 

  • Yamada I., Kurosawa K., Hasegawa H., Sakaniwa K. (1998) Algebraic multidimensional phase unwrapping and zero distribution of complex polynomials—Characterization of multivariate stable polynomials. IEEE Transactions on Signal Processing 46: 1639–1664

    Article  MATH  MathSciNet  Google Scholar 

  • Yamada I., Bose N. K. (2002) Algebraic phase unwrapping and zero distribution of polynomial for continuous-time systems. IEEE Transactions on Circuits and Systems—1: Fundamental Theory and Applications 49: 298–304

    Article  MathSciNet  Google Scholar 

  • Yamada, I. (2005, May). High-resolution DOA estimation by algebraic phase unwrapping algorithm. In Proceedings of IEEE ISCAS’05 (pp. 2413–2416).

  • Yamada, I., & Oguchi, K. (2005, December). Symbolic computation of DOA distribution by algebraic phase unwrapping. In Asian symposium on computer mathematics (ASCM). Seoul: KIAS.

  • Zetterberg P., Ottersten B. (1995) The spectrum efficiency of a base station antenna array system for spatially selective transmission. IEEE Transactions on Vehicle Technology 44: 651–660

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Communications and Integrated Systems, Tokyo Institute of Technology, 2-12-1-S3-60 Ookayama Meguro-ku, Tokyo, 152-8550, Japan

    Isao Yamada & Kazuhiro Oguchi

Authors
  1. Isao Yamada
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Kazuhiro Oguchi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Isao Yamada.

Additional information

This paper was made by the 1st author, in memory of Professor Nirmal Kumar Bose, based on partially the authors’ joint work during the 2nd author was at the Tokyo Institute of Technology. Currently, the 2nd author is with the Sony Corporation.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yamada, I., Oguchi, K. High-resolution estimation of the directions-of-arrival distribution by algebraic phase unwrapping algorithms. Multidim Syst Sign Process 22, 191–211 (2011). https://doi.org/10.1007/s11045-010-0141-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11045-010-0141-0

Keywords