Skip to main content

Advertisement

Springer Nature Link
Log in

The delay-range-dependent robust stability analysis for 2-D state-delayed systems with uncertainty

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

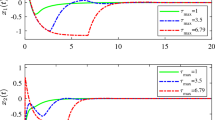
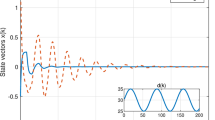
This paper addresses the problems of delay-range-dependent stability and robust stability for uncertain two-dimensional (2-D) state-delayed systems in the Fornasini–Machesini second model, with the uncertainty assumed to be of norm bounded form. A generalized Lyapunov function candidate is introduced to prove the stability condition and some free-weighting matrices are used for less conservative conditions. The resulting stability and robust stability conditions in terms of linear matrix inequalities are delay-range-dependent. Some numerical examples are given to illustrate the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Chen, S., & Fong, I. (2006). A delay-dependent approach to H ∞ filtering for 2-D state-delayed systems. In: Proceedings 45th IEEE conference on systems and control in aerospace and astronautics (pp. 540–544).

  • Chen S., Fong I. (2007) Delay-dependent robust H ∞ filtering for uncertain 2-D state-delayed systems. Signal Processing 87(11): 2659–2672

    Article  MATH  Google Scholar 

  • Feng Z., Xu L., Wu M., He Y. (2010) Delay-dependent robust stability and stabilisation of uncertain two-dimensional discrete systems with time-varying delays. IET Control Theory and Applications 10(4): 1959–1971

    Article  MathSciNet  Google Scholar 

  • He Y., Wang Q., Lin C., Wu M. (2007) Delay-range-dependent stability for systems with time-varying delay. Automatica 43(2): 371–376

    Article  MathSciNet  MATH  Google Scholar 

  • Hinamoto, T. (1989). The Fornasini–Marchesini model with no overflow oscillations and its application to 2-D digital filter design. In Proceedings IEEE international symposium on circuits and systems 1680–1683.

  • Mahmoud M. (2000) Robust control and filtering for time-delay systems. Control engineering series. Marcel Dekker, New York

    Google Scholar 

  • Paszke W., Lam J., Galkowski K., Xu S., Lin Z. (2004) Robust stability and stabilisation of 2D discrete state-delayed systems. Systems and Control Letters 51(3–4): 277–291

    Article  MathSciNet  MATH  Google Scholar 

  • Paszke, W., Lam, J., Galkowski, K., Xu, S., Rogers, E., & Kummert, A. (2006a). Delay-dependent stability of 2D state-delayed linear systems. In Proceedings IEEE international symposium on circuits and systems (pp. 2813–2816).

  • Paszke, W., Lam J., Galkowski, K., Xu, S., & Kummert, A. (2006b). Delay-dependent stability condition for uncertain linear 2-D state-delayed systems. In Proceedings 45th IEEE conference on decision and control (pp. 2783–2788).

  • Peng D., Guan X. (2009a) Output feedback H ∞ control for 2-D state-delayed systems. Circuits, Systems, and Signal Processing 28(1): 147–167

    Article  MathSciNet  MATH  Google Scholar 

  • Peng D., Guan X. (2009b) H ∞ filtering of 2-D discrete state-delayed systems. Multidimensional Systems and Signal Processing 20(3): 265–284

    Article  MathSciNet  MATH  Google Scholar 

  • Petersen I., Hollot C. (1986) A Riccati equation approach to the stabilization of uncertain linear systems. Automatica 22(4): 397–411

    Article  MathSciNet  MATH  Google Scholar 

  • Wu L., Wang Z., Gao H., Wang C. (2007) Filtering for uncertain 2-D discrete systems with state delays. Signal Processing 87(9): 2213–2230

    Article  MATH  Google Scholar 

  • Xie L., Lu L., Zhang D., Zhang H. (2004) Improved robust H 2 and H ∞ filtering for uncertain discrete-time systems. Automatica 40(5): 873–880

    Article  MathSciNet  MATH  Google Scholar 

  • Xu S., Lam J. (2005) Improved delay-dependent stability criteria for time-delay systems. IEEE Transactions on Automatic Control 50(3): 384–387

    Article  MathSciNet  Google Scholar 

  • Xu, H., Guo, L., Zou, Y., & Xu, S. (2007). Stability analysis for two-dimensional discrete delayed systems described by general models. In Proceedings IEEE international conference on control and automation (pp. 942–945).

  • Xu H., Xu S., Lam J. (2008) Positive real control for 2-D discrete delayed systems via output feedback controllers. Journal of Computational and Applied Mathematics 216(1): 87–97

    Article  MathSciNet  MATH  Google Scholar 

  • Xu J., Yu L. (2009a) Delay-dependent H ∞ control for 2-D discrete state delay systems in the second FM model. Multidimensional Systems and Signal Processing 20(4): 333–349

    Article  MathSciNet  Google Scholar 

  • Xu J., Yu L. (2009b) Delay-dependent guaranteed cost control for uncertain 2-D discrete systems with state delay in the FM second model. Journal of the Franklin Institute 346(2): 159–174

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang L., Wang C., Gao H. (2007) Delay-dependent stability and stabilization of a class of linear switched time-varying delay systems. Journal of Systems Engineering and Electronics 18(2): 320–326

    Article  MATH  Google Scholar 

  • Zhu X., Yang G. (2008) Delay-dependent stability criteria for systems with differentiable time delays. Acta Automatica Sinica 34(7): 765–771

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Automation, Nanjing University of Science and Technology, Nanjing, 210094, People’s Republic of China

    Juan Yao & Yun Zou

  2. Department of Mathematics, Nanjing University of Science and Technology, Nanjing, 210094, People’s Republic of China

    Weiqun Wang

Authors
  1. Juan Yao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Weiqun Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yun Zou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Juan Yao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yao, J., Wang, W. & Zou, Y. The delay-range-dependent robust stability analysis for 2-D state-delayed systems with uncertainty. Multidim Syst Sign Process 24, 87–103 (2013). https://doi.org/10.1007/s11045-011-0156-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11045-011-0156-1

Keywords