Abstract
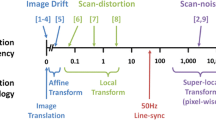
Transmission electron microscopes (TEMs) are the tools of choice in materials science, semiconductor, and biological research and it is expected that they will be increasingly used to autonomously perform high-volume, repetitive, nano-measurements in the near future. Thus, there is a clear need to develop automation strategies for these microscopes. In particular, an important feature in need of automation is specimen drift compensation, which is a common cause of image blurring in long-exposure TEM images, especially at high magnifications. In this paper, a systematic online approach to specimen drift compensation, called adaptive minimum variance control, is discussed in detail. The method makes use of an identified drift model, continuously updated from online drift measurements, to predict and ameliorate future drift values, significantly reducing their variance. The method’s performance, measured in terms of drift variance reduction, is illustrated using both experimental and simulated data, and it is then compared with the performance of two pragmatic model-free methods: last data point prediction and linear extrapolation prediction.







Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
Random variables and processes are denotes in boldfaced fonts, \(\mathbb N \) denotes the non-negative integers, and \(\mathbb N ^*\) denotes the positive integers.
With a slight abuse of notation, \(\mathcal H (B)\) and \(\mathcal H _c(B)\) will also denote the transfer functions \(\mathcal H (z)\) and \(\mathcal H _c(z)\) as in Fig. 3.
We gratefully acknowledge Dr. Richard Doornbos (Embedded Systems Institute) and Dr. Seyno Sluyterman (FEI Company) for their support in recording these images.
Other experimental parameters of interest are: pixel size, 2.1 nm/pixel; defocus, \(4.37\,\upmu \hbox {m}\); electron dose, 144–148 e/nm\(^2\)s; spot size, 10; specimen, gold on carbon foil.
References
Akaike, H. (1970). A fundamental relation between predictor identification and power spectrum estimation. Annals of the Institute of Statistical Mathematics, 22(1), 219–223.
Åström, K. J. (1967). Computer control of a paper machine: An application of linear stochastic control theory. IBM Journal of Research and Development, 11(4), 389–405.
Åström, K. J. (1970). Introduction to stochastic control theory. New York, NY: Academic Press.
Åström, K. J., & Wittenmark, B. (1973). On self tuning regulators. Automatica, 9(2), 185–199.
Åström, K. J., & Wittenmark, B. (1995). Adaptive control reading. Massachusetts: Addison-Wesley.
Basu, P., Rudoy, D., & Wolfe, P. J. (2009). A nonparametric test for stationarity based on local Fourier analysis. In Proceedings of the 2009 IEEE international conference on acoustics, speech and signal processing (pp. 3005–3008). Taipei, Taiwan.
Bloomfield, P. (1972). On the error of prediction of a time series. Biometrika, 59(3), 501–507.
Box, G. E. P., Jenkins, G. M., & Reinsel, G. C. (1976). Time series analysis: Forecasting and control. Oakland, CA: Holden-Day.
Broersen, P. M. T. (2002). Automatic spectral analysis with time series models. IEEE Transactions on Instrumentation and Measurement, 51(2), 211–216.
Broersen, P. M. T. (2006). Automatic autocorrelation and spectral analysis. London: Springer.
Broersen, P. M. T. (2009). ARMASA toolbox for Matlab. http://goo.gl/jMNWK.
De Graef, M. (2003). Introduction to conventional transmission electron microscopy. Cambridge: Cambridge University Press.
Durbin, J. (1960). The fitting of time series models. Revue de l’Institut International de Statistique, 28(3), 233–243.
Erkelens, J. S., Tejada, A., & den Dekker, A. J. (2013). Identification of time series models from segments: Application to scanning transmission electron microscopy images. IEEE Transactions on Instrumentation and Measurement, 62, to appear.
Franklin, G. F., Powell, J. D., & Workman, M. L. (1998). Digital control of dynamical systems (3rd ed.). Menlo Park, CA: Addison-Wesley.
Hamilton, J. D. (1994). Time series analysis. Princeton, NJ: Princeton University Press.
Hannan, E. J. (1987). Rational transfer function approximation. Statistical Science, 2(2), 135–151.
Howe, J. M. (2008). In-situ HRTEM studies of interface dynamics during solid-solid phase transformations in metal alloys. In F. Banhart (Ed.), In-situ electron microcopy at high-resolution (pp. 167–186). Singapore: World Scientific.
Inada, H., Kakibayashi, H., Isakozawa, S., Hashimoto, T., Yaguchi, T., & Nakamura, K. (2009). Hitachi’s development of cold-field emission scanning transmission electron microscopes. In P. W. Hawkes (Ed.), Cold field emission and the scanning transmission electron microscope, advances in imaging and electron physics (Vol. 159, pp. 123–186). London: Elsevier.
Kwiatkowski, D., Phillips, P. C. B., Schmidt, P., & Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics, 54(1–3), 159–178.
Li, Z., & Evans, R. (1997). Minimum-variance control of linear time-varying systems. Automatica, 33(8), 1531–1537.
Liu, Z., & Gu, W. (2004). High-speed and high-precision deflectors applied in electron beam lithography system based on scanning electron microscopy. Journal of Vacuum Science and Technology. B: Microelectronics and Nanometer Structures, 22(6), 3557–3559.
Pfaff, B. (2008). Analysis of integrated and cointegrated time series with R (2nd ed.). New York, NY: Springer.
Phillips, P. C. B., & Perron, P. (1988). Testing for a unit root in time series regression. Biomètrika, 75(2), 335–346.
Plitzko, J. M., & Mayer, J. (1999). Quantitative thin film analysis by energy filtering transmission electron microscopy. Ultramicroscopy, 78(1–4), 207–219.
Priestley, M. B. (1981a). Spectral analysis and time series (Vol. 1). New York, NY: Academic Press.
Priestley, M. B. (1981b). Spectral analysis and time series (Vol. 2). New York, NY: Academic Press.
Pulokas, J., Green, C., Kisseberth, N., Potter, C. S., & Carragher, B. (1999). Improving the positional accuracy of the goniometer on the philips CM series TEM. Journal of Structural Biology, 128(3), 250–256.
Reimer, L. (1993). Transmission electron micrsocopy. Physics of image formation and microanalysis (3rd ed.). Berlin, Heidelberg: Springer.
Sachs, D., Nasiri, S., & Goehl, D. (2006). Image stabilization technology overview. http://goo.gl/YVHiN, White Paper.
Saka, H. (2008). In-situ high-resolution observation of solid–solid, solid–liquid and solid–gas reactions. In F. Banhart (Ed.), In-situ electron microcopy at high-resolution. Singapore: World Scientific.
Shan, Q., Jia, J., & Agarwala, A. (2008). High-quality motion deblurring from a single image. ACM Transactions on Graphics (SIGGRAPH), 27(3), article 73.
Sigle, W., Krämer, S., Varshney, V., Zern, A., Eigenthaler, U., & Rühle, M. (2003). Plasmon energy mapping in energy-filtering transmission electron microscopy. Ultramicroscopy, 96(3–4), 565–571.
Snella, M. T. (2010). Drift correction for scanning-electron microscopy. Master’s thesis. Boston, MA: Massachusetts Institute of Technology.
Spence, J. C. H. (2003). High-resolution electron microscopy (3rd ed.). New York, NY: Oxford University Press.
Tarău, A. N., Nuij, P., & Steinbuch, M. (2011a). Hierarchical control for drift correction in transmission electron microscopes. In Proceedings of the 20th IEEE international conference on control applications (pp. 351–356). Denver, CO.
Tarău, A. N., Nuij, P., & Steinbuch, M. (2011b). Model-based drift control for electron microscopes. In Proceedings of the 18th IFAC World Congress (pp. 8583–8588). Milano, Italy.
Tejada, A., & den Dekker, A. J. (2011). POEM: A fast defocus estimation method for scanning transmission electron microscopy. In Proceedings of the 2011 IEEE international instrumentation and measurement technology conference (pp. 1228–1232). Hangzhou, China.
Tejada, A., & den Dekker, A. J. (2012). Defocus polar rose estimation method (POEM): A fast defocus estimation method for STEM. IEEE Transactions on Instrumentation and Measurement, 61(10), 2723–2730.
Tejada, A., Van Den Broek, W., van der Hoeven, S., & den Dekker, A. J. (2009a). Towards STEM control: Modeling framework and development of a sensor for defocus control. In Proceedings of 48th IEEE conference on decision and control (pp. 8310–8315). Shanghai, China.
Tejada, A., van der Hoeven, S. W., den Dekker, A. J., & Van den Hof, P. M. J. (2009b). Towards automatic control of scanning transmission electron microscopes. In Proceedings of the 18th IEEE international conference on control applications (pp. 788–793). Saint Petersburg, Russia.
Tejada, A., den Dekker, A. J., & Van Den Broek, W. (2011a). Introducing measure-by-wire, the systematic use of systems and control theory in transmission electron microscopy. Ultramicroscopy, 111(11), 1581–1591.
Tejada, A., Vos, P., & den Dekker, A. J. (2011b). Towards an adaptive minimum variance control scheme for specimen drift compensation in transmission electron microscopes. In Proceedings of 7th international workshop on multidimensional (nD) systems. Poitiers, France.
Tsuneta, R., Koguchi, M., Nakamura, K., & Nishida, A. (2002). A specimen-drift-free EDX mapping system in a STEM for observing two-dimensional profiles of low dose elements in fine semiconductor devices. Journal of Electron Microscopy, 51(3), 167–171.
Williams, D. B., & Carter, C. B. (2009). Transmission electron microscopy. A textbook for materials science. New York, NY: Springer.
Yamamoto, T. (1975). Asymptotic mean square error of multi-step prediction from mixed autoregressive moving average model. CORE Discussion Papers No. 7521, Center for Operations Research & Econometrics, Heverlee, Belgium.
Yang, Q., Jagannathan, S., & Bohannan, E. W. (2008). Automatic drift compensation using phase correlation method for nanomanipulation. IEEE Transactions on Nanotechnology, 7(2), 209–216.
Zhang, W. (2010). On the stability and convergence of self-tuning controlvirtual equivalent system approach. International Journal of Control, 83(5), 879–896.
Zitová, B., & Flusser, J. (2003). Image registration methods: A survey. Image and Vision Computing, 21(11), 977–1000.
Acknowledgments
This research was sponsored by the Condor project at FEI company, under the responsibilities of the Embedded Systems Institute (ESI). This project is partially supported by the Dutch Ministry of Economic Affairs under the BSIK program. The authors also gratefully acknowledge the instructive technical discussions on control theory held with Dr. Stefan Kuiper (TNO) and Dr. Xavier Bombois (Delft University of Technology), the simulation support of Ir. Pauline Vos (NLS), the insights on TEM imaging provided by Dr. Wouter Van den Broek (Ulm University), and the technical discussions on ARMASA with Dr. Piet M.T. Broersen and Dr. Jan S. Erkelens.
Author information
Authors and Affiliations
Corresponding author
Appendix: Determination of stationarity properties of time series
Appendix: Determination of stationarity properties of time series
Determining a time series’ stationarity properties is a well established subject of study, specially in econometrics. The best understood stationarity tests are those by Phillips and Perron (1988) (PP) and Kwiatkowski et al. (1992) (KPSS), which assume the time series to be generated by either model (2), (7), or (8) (with \(d=1\)) (for tests without this assumption see, e.g., Basu et al. 2009). Both tests use hypothesis testing and can discern a stationary time series with constant mean from one with a linear trend or one with a unit root. Moreover, these tests are complementary, since they have opposite null hypotheses (KPSS’s is that the time series is stationary, while PP’s is that the series has a unit root), and can be used to reinforce each other’s conclusions.
Both tests were applied to the experimental drift realizations described in Sect. 4 in three steps, making use of the fact that differencing a process with deterministic trend does not yield a stationary process. Thus, in the first step the test were applied, with a 99 % significance level, to the second difference of each experimental drift realization. In each of the 20 cases, the PP null hypothesis was rejected while the KPSS null hypothesis could not be rejected. This strongly suggested that the experimental drift realizations were generated by either an ARMA\((p,q)\), ARIMA\((p,1,q)\), or ARIMA\((p,2,q)\) process and not by a process with deterministic trend. To eliminate the ARIMA\((p,2,q)\) possibility, in the second step the tests were applied to the the first difference of each experimental drift realization. The tests results, shown in Table 5, strongly suggest that the drift is not generated by an ARIMA\((p,2,q)\) process (since most first-difference series seem to be stationary). The highlighted results (red solid boxes) in this table indicate instances where the PP and KPSS tests contradict each other, so no decision can be made. However, in each of these instances the companion pair of tests (i.e., those shown in the same row, adjacent column) applied to the same experimental drift realizations do allow for a decision. Note that in most cases, both the constant level and linear trend KPSS give positive results, which seems to indicate the absence of a linear trend in the first-difference data. To make the final determination, in the third step the tests were applied to the experimental drift realizations directly. The test results are shown in Table 6. It follows immediately from this table that realizations \(RL_0^x,\, RL_0^y,\, RL_1^x,\, RL_2^x,\, RL_2^y,\, RL_3^x,\, RL_3^y,\, RL_4^x,\, RL_4^y,\, U\!D_0^x\), and \(U\!D_3^x\) seem to come from an ARIMA\((p,1,q)\) process with constant mean. The results provide contradictory information for realizations \(U\!D_0^y,\, U\!D_1^x,\, U\!D_2^y\) (green shaded boxes) that seems to suggest that these series may be barely stationary (i.e., they may have a root very close to the unitary circle). The results also suggest that realizations \(U\!D_1^y\) and \(U\!D_4^y\) may come from a stationary process and, finally, that no final decision can be reached for realizations \(RL_1^y,\, U\!D_2^y,\, U\!D_3^y\), and \(U\!D_4^x\) (black dashed boxes) based on the results of these tests (although Table 5 suggests that there is no loss in generality in assuming these realizations came from an ARIMA\((p,1,q)\) process). In conclusion, most realizations seem to come from an ARIMA\((p,1,q)\) process.
Rights and permissions
About this article
Cite this article
Tejada, A., den Dekker, A.J. A comparison between minimum variance control and other online compensation methods for specimen drift in transmission electron microscopy. Multidim Syst Sign Process 25, 247–271 (2014). https://doi.org/10.1007/s11045-013-0246-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11045-013-0246-3