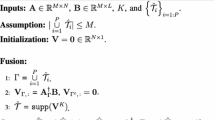Split Bregman algorithms for multiple measurement vector problem

Abstract

The standard sparse representation aims to reconstruct sparse signal from single measurement vector which is known as SMV model. In some applications, the SMV model extend to the multiple measurement vector (MMV) model, in which the signal consists of a set of jointly sparse vectors. In this paper, efficient algorithms based on split Bregman iteration are proposed to solve the MMV problems with both constrained form and unconstrained form. The convergence of the proposed algorithms is also discussed. Moreover, the proposed algorithms are used in magnetic resonance imaging reconstruction. Numerical results show the effectiveness of the proposed algorithms.

Appendices

Appendix 1: Proof of theorem 1

proof

The main idea of this proof is from the one in Cai et al. (2009). However, this proof is much different due to the matrix variable and the mixed norm.

Since subproblems (17) and (18) are convex, the first order optimality condition of Algorithm 1 gives as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf 0 = \lambda \mathbf A ^T (\mathbf A \mathbf X ^{k+1}-\mathbf Y ) + \mu (\mathbf X ^{k+1}-\mathbf Z ^k+\mathbf B ^k), \\ \mathbf 0 = \mathbf P ^{k+1}+ \mu (\mathbf Z ^{k+1}-\mathbf X ^k-\mathbf B ^k), \\ \mathbf B ^{k+1} = \mathbf B ^k + (\mathbf X ^{k+1} - \mathbf Z ^{k+1}),\\ \end{array} \right. \end{aligned}$$

(34)

where $\mathbf P ^{k+1} \in \partial \Vert \mathbf Z \Vert _{2,1} \mid _\mathbf{Z = \mathbf Z ^{k+1} }$, for ease of notations, we just denote $\mathbf P ^{k+1} \in \partial \Vert \mathbf Z ^{k+1} \Vert _{2,1}$ in the remainder of this paper. The subgradient of $\Vert \cdot \Vert _{2,1}$ can be seen in Appendix 3.

Since there exists at least one solution $\mathbf X ^*$ of (3) by the assumption, by the first order optimality condition, $\mathbf X ^*$ must satisfy

$$\begin{aligned} \mathbf P ^* + \mathbf A ^T(\mathbf A \mathbf X ^{*}-\mathbf Y ) = 0, \end{aligned}$$

(35)

where $\mathbf P ^{*} \in \partial \Vert \mathbf Z ^{*} \Vert _{2,1}$ and $\mathbf Z ^{*} = \mathbf X ^{*}$.

Let $\mathbf B ^* = \mathbf P ^*/ \mu$. Then (35) can be formulated as

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf 0 = \lambda \mathbf A ^T (\mathbf A \mathbf X ^{*}-\mathbf Y ) + \mu (\mathbf X ^{*}-\mathbf Z ^*+\mathbf B ^*), \\ \mathbf 0 = \mathbf P ^{*}+ \mu (\mathbf Z ^{*}-\mathbf X ^*-\mathbf B ^*), \\ \mathbf B ^{*} = \mathbf B ^* + (\mathbf X ^{*} - \mathbf Z ^{*}).\\ \end{array} \right. \end{aligned}$$

(36)

Comparing (36) with (34), $(\mathbf X ^{*}, \mathbf Z ^{*}, \mathbf B ^{*})$ is a fixed point of Algorithm 1. Similar like the paper by Goldstein and Osher (2009), if the unconstrained spilt Bregman iteration converges, it converges to a solution of (3).

Denote the errors by $\mathbf X _e^{k} = \mathbf X ^{k}-\mathbf X ^{*}$, $\mathbf Z _e^{k} = \mathbf Z ^{k}-\mathbf Z ^{*}$ and $\mathbf B _e^{k} = \mathbf B ^{k}-\mathbf B ^{*}$. Subtracting the first equation of (34) by the first equation of (36), we obtain

$$\begin{aligned} \mathbf 0 = \lambda \mathbf A ^T \mathbf A \mathbf X _e^{k+1} + \mu (\mathbf X _e^{k+1}-\mathbf Z _e^k+\mathbf B _e^k). \end{aligned}$$

(37)

Taking the inner product of the left- and right-hand sides with $\mathbf X _e^{k+1}$, we have

$$\begin{aligned} \mathbf 0 = \lambda \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 + \mu \Vert \mathbf X _e^{k+1} \Vert _F^2 - \mu \langle \mathbf Z _e^k, \mathbf X _e^{k+1} \rangle + \mu \langle \mathbf B _e^k, \mathbf X _e^{k+1} \rangle . \end{aligned}$$

(38)

Similarly, subtracting the second equation of (34) by the second equation of (36) and then taking the inner product of the left- and right- hand sides with $\mathbf Z _e^{k+1}$, we have

$$\begin{aligned} \mathbf 0 = \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle + \mu \Vert \mathbf Z _e^{k+1} \Vert _F^2 - \mu \langle \mathbf Z _e^{k+1}, \mathbf X _e^{k+1} \rangle - \mu \langle \mathbf B _e^k, \mathbf Z _e^{k+1} \rangle \end{aligned}$$

(39)

where $\mathbf P ^{k+1} \in \partial \Vert \mathbf Z ^{k+1} \Vert _{2,1}$, $\mathbf P ^{*} \in \partial \Vert \mathbf Z ^{*} \Vert _{2,1}$.

Adding both sides of (38) to the corresponding sides of (39), we have

$$\begin{aligned} \mathbf 0&= \lambda \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 + \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle \nonumber \\&+\, \mu \left( \Vert \mathbf X _e^{k+1} \Vert _F^2 + \Vert \mathbf Z _e^{k+1} \Vert _F^2 - \langle \mathbf X _e^{k+1},\mathbf Z _e^{k+1}+\mathbf Z _e^{k} \rangle + \langle \mathbf B _e^k, \mathbf X _e^{k+1}-\mathbf Z _e^{k+1} \rangle \right) . \end{aligned}$$

(40)

Furthermore, by subtracting the third equation of (34) by the corresponding one in (36), we obtain

$$\begin{aligned} \mathbf B _e^{k+1} = \mathbf B _e^k + \mathbf X _e^{k+1} - \mathbf Z _e^{k+1}. \end{aligned}$$

(41)

Taking square norm of both sides of (41), we obtain

$$\begin{aligned} \Vert \mathbf B _e^{k+1}\Vert _F^2 = \Vert \mathbf B _e^k\Vert _F^2 + \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k+1} \Vert _F^2 + 2\langle \mathbf B _e^k, \mathbf X _e^{k+1} - \mathbf Z _e^{k+1}\rangle , \end{aligned}$$

(42)

and further

$$\begin{aligned} \langle \mathbf B _e^k, \mathbf X _e^{k+1} - \mathbf Z _e^{k+1}\rangle = \frac{1}{2}(\Vert \mathbf B _e^{k+1}\Vert _F^2 - \Vert \mathbf B _e^k\Vert _F^2 - \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k+1}\Vert _F^2). \end{aligned}$$

(43)

Substituting (43) into (40), we have

$$\begin{aligned}&\frac{\mu }{2}(\Vert \mathbf B _e^{k}\Vert _F^2 - \Vert \mathbf B _e^{k+1}\Vert _F^2) = \lambda \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 + \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle \nonumber \\&\quad \quad + \mu (\Vert \mathbf X _e^{k+1} \Vert _F^2 + \Vert \mathbf Z _e^{k+1} \Vert _F^2 - \langle \mathbf X _e^{k+1},\mathbf Z _e^{k+1}+\mathbf Z _e^{k} \rangle - \frac{1}{2} \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k+1}\Vert _F^2) \nonumber \\&\quad = \lambda \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 + \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle \!+\! \frac{\mu }{2} (\Vert \mathbf X _e^{k+1} \!-\! \mathbf Z _e^{k} \Vert _F^2 + \Vert \mathbf Z _e^{k+1} \Vert _F^2 - \Vert \mathbf Z _e^{k}\Vert _F^2).\nonumber \\ \end{aligned}$$

(44)

Summing (44) from $k=0$ to $k=K$, it yields

$$\begin{aligned} \frac{\mu }{2}(\Vert \mathbf B _e^{0}\Vert _F^2 - \Vert \mathbf B _e^{K+1}\Vert _F^2&= \lambda \sum _{k=0}^K \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 + \sum _{k=0}^K \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle \nonumber \\&+ \frac{\mu }{2} (\sum _{k=0}^K \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 + \Vert \mathbf Z _e^{K+1} \Vert _F^2 - \Vert \mathbf Z _e^{0}\Vert _F^2). \end{aligned}$$

(45)

Since $\mathbf P ^{k+1} \in \partial \Vert \mathbf X ^{k+1} \Vert _{2,1}$, $\mathbf P ^{*} \in \partial \Vert \mathbf X ^{*} \Vert _{2,1}$ and $\Vert \cdot \Vert _{2,1}$ is convex, for $\forall k$,

$$\begin{aligned} \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle&= \Vert \mathbf Z ^{k+1} \Vert _F^2 - \Vert \mathbf Z ^{*}\Vert _F^2 - \langle \mathbf P ^{*}, \mathbf Z _e^{k+1}-\mathbf Z _e^{*}\rangle \nonumber \\&+ \Vert \mathbf Z ^{*} \Vert _F^2 - \Vert \mathbf Z ^{k+1}\Vert _F^2 - \langle \mathbf P ^{k+1}, \mathbf Z ^{*}-\mathbf Z ^{k+1}\rangle \ge 0. \end{aligned}$$

(46)

Therefore, all terms involved in (45) are nonnegative. We have

$$\begin{aligned}&\frac{\mu }{2}\Vert \mathbf B _e^{0}\Vert _F^2 + \frac{\mu }{2} \Vert \mathbf Z _e^{0}\Vert _F^2 \nonumber \\&\quad \ge \frac{\lambda }{2} \sum _{k=0}^K \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 + \sum _{k=0}^K \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle + \frac{\mu }{2} (\sum _{k=0}^K \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 ).\qquad \end{aligned}$$

(47)

From (47) and $\mu >0$, $\lambda >0$, we can get

$$\begin{aligned} \sum _{k=0}^{+ \infty } \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 < + \infty . \end{aligned}$$

(48)

(48) imply that $\lim _{k\rightarrow + \infty } \Vert \mathbf A \mathbf X _e^{k} \Vert _F^2 =0$, and

$$\begin{aligned}&\lim _{k\rightarrow + \infty } \Vert \mathbf A \mathbf X _e^{k} \Vert _F^2 = \lim _{k\rightarrow + \infty } \Vert \mathbf A \mathbf X ^{k} - \mathbf A \mathbf X ^{*}\Vert _F^2\nonumber \\&\quad = \lim _{k\rightarrow + \infty } \langle \mathbf A ^T(\mathbf A \mathbf X ^{k}-\mathbf A \mathbf X ^{*}), \mathbf X ^{k} - \mathbf X ^{*} \rangle = 0. \end{aligned}$$

(49)

Recall the definition of the Bregman distance, for any convex function $J$, we have

$$\begin{aligned} D_J^\mathbf{P }(\mathbf X ,\mathbf Z ) + D_J^\mathbf{Q }(\mathbf Z ,\mathbf X ) = \langle \mathbf Q -\mathbf P , \mathbf X -\mathbf Z \rangle \end{aligned}$$

(50)

where $\mathbf P \in \partial J(\mathbf Z )$ and $\mathbf Q \in \partial J(\mathbf X )$.

Now let $J(\mathbf X ) = \frac{1}{2}\Vert \mathbf{AX-Y }\Vert _F^2$, $\nabla J(\mathbf X ) = \mathbf A ^T(\mathbf{AX-Y })$, from (50) we have

$$\begin{aligned} D_J^{\nabla J(\mathbf X ^{*})}(\mathbf X ^k,\mathbf X ^*) + D_J^{\nabla J(\mathbf X ^{k})}(\mathbf X ^*,\mathbf X ^k) = \langle \mathbf A ^T(\mathbf A \mathbf X ^{k}-\mathbf A \mathbf X ^{*}), \mathbf X ^{k} - \mathbf X ^{*} \rangle = 0. \end{aligned}$$

(51)

(51) together with the nonnegativity of the Bregman distance, implies that

$$\begin{aligned} \lim _{k\rightarrow + \infty } D_J^{\nabla J(\mathbf X ^{*})}(\mathbf X ^k,\mathbf X ^*) =0, \end{aligned}$$

(52)

i.e.,

$$\begin{aligned} \lim _{k\rightarrow + \infty } \frac{1}{2}\Vert \mathbf A \mathbf X ^{k} - \mathbf Y \Vert _F^2 - \frac{1}{2}\Vert \mathbf A \mathbf X ^{*} - \mathbf Y \Vert _F^2 - \langle \mathbf A ^T(\mathbf A \mathbf X ^{*}-\mathbf Y ), \mathbf X ^{k} - \mathbf X ^{*} \rangle = 0. \end{aligned}$$

(53)

Similarly, (47) also leads to

$$\begin{aligned} \sum _{k=0}^{+ \infty } \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle < + \infty , \end{aligned}$$

(54)

and hence

$$\begin{aligned} \lim _{k\rightarrow + \infty } \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle =0. \end{aligned}$$

(55)

Let $J(\mathbf Z ) = \Vert \mathbf Z \Vert _{2,1}$ and $\mathbf P \in \partial \Vert \mathbf Z \Vert _{2,1}$, we can get $\lim _{k\rightarrow + \infty } D_{\Vert \cdot \Vert _{2,1}}^\mathbf{P ^*}(\mathbf Z ^k,\mathbf Z ^*) =0$, i.e.,

$$\begin{aligned} \lim _{k\rightarrow + \infty } \Vert \mathbf Z ^k \Vert _{2,1} - \Vert \mathbf Z ^* \Vert _{2,1} - \langle \mathbf Z ^{k}-\mathbf Z ^{*}, \mathbf P ^{*} \rangle = 0. \end{aligned}$$

(56)

Moreover, since $\mu >0$, (47) also leads to $\sum _{k=0}^{+ \infty } \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 < + \infty$, which implies that $\lim _{k\rightarrow + \infty } \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 = 0$. By $\mathbf X ^{*} = \mathbf Z ^{*}$, we conclude that

$$\begin{aligned} \lim _{k\rightarrow + \infty } \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2&= \lim _{k\rightarrow + \infty } \Vert \mathbf X ^{k+1} - \mathbf X ^{*} - \mathbf Z ^{k} + \mathbf Z ^{*} \Vert _F^2 \nonumber \\&= \lim _{k\rightarrow + \infty } \Vert \mathbf X ^{k+1} - \mathbf Z ^{k} \Vert _F^2 = 0. \end{aligned}$$

(57)

Since $\Vert \cdot \Vert _{2,1}$ is continuous, by (56) and (57), for $\mathbf X$, we have

$$\begin{aligned} \lim _{k\rightarrow + \infty } \Vert \mathbf X ^k \Vert _{2,1} - \Vert \mathbf X ^* \Vert _{2,1} - \langle \mathbf X ^{k}-\mathbf X ^{*}, \mathbf P ^{*} \rangle = 0. \end{aligned}$$

(58)

Adding (53) to (58), it yields

$$\begin{aligned} 0&= \lim _{k\rightarrow + \infty } \Vert \mathbf X ^k \Vert _{2,1} + \frac{\lambda }{2} \Vert \mathbf A \mathbf X ^k-\mathbf Y \Vert _F^2 \nonumber \\&\quad -\Vert \mathbf X ^* \Vert _{2,1} - \frac{\lambda }{2} \Vert \mathbf A \mathbf X ^*-\mathbf Y \Vert _F^2 - \langle \mathbf X ^{k}-\mathbf X ^{*}, \mathbf P ^{*}+\mathbf A ^T(\mathbf A \mathbf X ^{*}-\mathbf Y ) \rangle \nonumber \\&= \lim _{k\rightarrow + \infty } \Vert \mathbf X ^k \Vert _{2,1} + \frac{\lambda }{2} \Vert \mathbf A \mathbf X ^k-\mathbf Y \Vert _F^2 - \Vert \mathbf X ^* \Vert _{2,1} - \frac{\lambda }{2} \Vert \mathbf A \mathbf X ^*-\mathbf Y \Vert _F^2, \end{aligned}$$

(59)

where the last equality comes from (35). So (29) is proved.

Next, we prove (30) whenever (3) has a unique solution. It is proved by contradiction.

Define $\varPhi (\mathbf X ) = \Vert \mathbf X \Vert _{2,1} + \Vert \mathbf{AX-Y }\Vert _F^2$. Then $\varPhi (\mathbf X )$ is convex and lower semi-continuous. Since $\mathbf X ^*$ is the unique minimizer, we have $\varPhi (\mathbf X ^*) > \varPhi (\mathbf X )$ for $\mathbf X \ne \mathbf X ^*$.

Now, suppose that (30) does not hold. So, there exists a subsequence $\mathbf X ^{k_i}$ such that $\Vert \mathbf X ^{k_i} - \mathbf X ^{*}\Vert _F > \epsilon$ for some $\epsilon > 0$ and all $i$. Then, $\varPhi (\mathbf X ^{k_i}) > \min \{ \varPhi (\mathbf X ) : \Vert \mathbf X ^{k_i} - \mathbf X ^{*}\Vert _F = \epsilon \}$. Let $\mathbf Z$ be the intersection of $\{ \mathbf X : \Vert \mathbf X - \mathbf X ^{*}\Vert _F = \epsilon \}$ and the line from $\mathbf X ^{*}$ to $\mathbf X ^{k_i}$. Indeed, there exists a positive number $t \in (0,1)$ such that $\mathbf Z = t \mathbf X ^{*} + (1-t) \mathbf X ^{k_i}$. By the convexity of $\varPhi$ and the definition of $\mathbf X ^{*}$, we have

$$\begin{aligned} \varPhi (\mathbf X ^{k_i}) >&= t \varPhi (\mathbf X ^{*}) + (1-t) \varPhi (\mathbf X ^{k_i}) \ge \varPhi (t \mathbf X ^{*} + (1-t) \mathbf X ^{k_i}) = \varPhi (\mathbf Z ) \nonumber \\&\ge \min \{ \varPhi (\mathbf X ) : \Vert \mathbf X ^{k_i} - \mathbf X ^{*}\Vert _F = \epsilon \}. \end{aligned}$$

(60)

Denote ${\tilde{\mathbf{X }}} = \min \{ \varPhi (\mathbf X ) : \Vert \mathbf X ^{k_i} - \mathbf X ^{*}\Vert _F = \epsilon \}$. By (29), we have

$$\begin{aligned} \varPhi (\mathbf X ^*) = \lim _{k\rightarrow + \infty } \varPhi (\mathbf X ^{k_i}) \ge \varPhi ({\tilde{\mathbf{X }}}) > \varPhi (\mathbf X ^*), \end{aligned}$$

(61)

which is a contradiction. So (30) holds whenever (3) has a unique solution. $\square$

Appendix 2: Proof of Theorem 2

proof

Since subproblems (26) and (27) are convex, the first order optimality condition of Algorithm 2 is given as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf 0 = \lambda \mathbf A ^T (\mathbf A \mathbf X ^{k+1}-\mathbf Y +\mathbf C ^k) + \mu (\mathbf X ^{k+1}-\mathbf Z ^k+\mathbf B ^k), \\ \mathbf 0 = \mathbf P ^{k+1}+ \mu (\mathbf Z ^{k+1}-\mathbf X ^k-\mathbf B ^k), \\ \mathbf C ^{k+1} = \mathbf C ^k + (\mathbf Y - \mathbf A \mathbf X ^{k+1}),\\ \mathbf B ^{k+1} = \mathbf B ^k + (\mathbf X ^{k+1} - \mathbf Z ^{k+1}),\\ \end{array} \right. \end{aligned}$$

(62)

where $\mathbf P ^{k+1} \in \partial \Vert \mathbf Z ^{k+1} \Vert _{2,1}$.

Let $L(\mathbf X ,\mathbf W ) = \Vert \mathbf X \Vert _{2,1} + \langle \mathbf W , \mathbf{AX-Y }\rangle$ be the Lagrangian of (2) and $\mathbf W$ be the Lagrangian multiplier. Since there exists at least one solution $\mathbf X ^*$ of (2) by the assumption, the KKT condition ensures the existence of a $\mathbf W ^*$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} \nabla _\mathbf{X } L(\mathbf X ^*,\mathbf W ^*) = \mathbf P ^* + \mathbf A ^T\mathbf W ^* = 0, \\ \nabla _\mathbf{W } L(\mathbf X ^*,\mathbf W ^*) = \mathbf A \mathbf X ^*-\mathbf Y = 0, \\ \end{array} \right. \end{aligned}$$

(63)

where $\mathbf P ^{*} \in \partial \Vert \mathbf X ^{*} \Vert _{2,1}$.

Let $\mathbf B ^* = \mathbf P ^*/ \mu$, $\mathbf C ^* = \mathbf W ^*/ \lambda$. Then (63) can be formulated as

$$\begin{aligned} \left\{ \begin{array}{ll} \mathbf 0 = \lambda \mathbf A ^T (\mathbf A \mathbf X ^{*}-\mathbf Y +\mathbf C ^*) + \mu (\mathbf X ^{*}-\mathbf Z ^*+\mathbf B ^*), \\ \mathbf 0 = \mathbf P ^{*}+ \mu (\mathbf Z ^{*}-\mathbf X ^*-\mathbf B ^*), \\ \mathbf C ^{*} = \mathbf C ^* + (\mathbf Y - \mathbf A \mathbf X ^{*}),\\ \mathbf B ^{*} = \mathbf B ^* + (\mathbf X ^{*} - \mathbf Z ^{*}).\\ \end{array} \right. \end{aligned}$$

(64)

Comparing (64) and (62), $(\mathbf X ^{*}, \mathbf Z ^{*}, \mathbf C ^{*}, \mathbf B ^{*})$ is a fixed point of Algorithm 2.

Denote the errors by $\mathbf X _e^{k} = \mathbf X ^{k}-\mathbf X ^{*}$, $\mathbf Z _e^{k} = \mathbf Z ^{k}-\mathbf Z ^{*}$, $\mathbf B _e^{k} = \mathbf B ^{k}-\mathbf B ^{*}$ and $\mathbf C _e^{k} = \mathbf C ^{k}-\mathbf C ^{*}$.

Similar to the corresponding part of the proof of Theorem 1,

we can get

$$\begin{aligned}&\frac{\lambda }{2}(\Vert \mathbf C _e^{0}\Vert _F^2 - \Vert \mathbf C _e^{K+1}\Vert _F^2) + \frac{\mu }{2}(\Vert \mathbf B _e^{0}\Vert _F^2 - \Vert \mathbf B _e^{K+1}\Vert _F^2)\nonumber \\&\quad = \frac{\lambda }{2} \sum _{k=0}^K \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 + \sum _{k=0}^K \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle \nonumber \\&\quad \quad + \frac{\mu }{2} (\sum _{k=0}^K \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 + \Vert \mathbf Z _e^{K+1} \Vert _F^2 - \Vert \mathbf Z _e^{0}\Vert _F^2). \end{aligned}$$

(65)

Note all terms involved in (65) are nonnegative. We have

$$\begin{aligned}&\frac{\lambda }{2}\Vert \mathbf C _e^{0}\Vert _F^2 + \frac{\mu }{2}\Vert \mathbf B _e^{0}\Vert _F^2 + \frac{\mu }{2} \Vert \mathbf Z _e^{0}\Vert _F^2 \nonumber \\&\quad \ge \frac{\lambda }{2} \sum _{k=0}^K \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 + \sum _{k=0}^K \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle + \frac{\mu }{2} (\sum _{k=0}^K \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 ).\qquad \end{aligned}$$

(66)

From (66) and $\mu >0$, $\lambda >0$, we can get

$$\begin{aligned} \sum _{k=0}^{+ \infty } \Vert \mathbf A \mathbf X _e^{k+1} \Vert _F^2 < + \infty . \end{aligned}$$

(67)

(67) and $\mathbf A \mathbf X _e^{k+1} = \mathbf A \mathbf X ^{k+1} - \mathbf Y$ leads to the first equation in (31) holding, i.e.,

$$\begin{aligned} \lim _{k\rightarrow + \infty } \Vert \mathbf A \mathbf X ^{k+1} - \mathbf Y \Vert _F^2 =0. \end{aligned}$$

(68)

Similarly, (67) also leads to

$$\begin{aligned} \sum _{k=0}^{+ \infty } \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z _e^{k+1}-\mathbf Z _e^{*}\rangle < + \infty , \end{aligned}$$

(69)

and hence

$$\begin{aligned} \lim _{k\rightarrow + \infty } \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle =0. \end{aligned}$$

(70)

Recall equation (50) and let $J(\mathbf Z )= \Vert \mathbf Z \Vert _{2,1}$, $\mathbf P \in \partial \Vert \mathbf Z \Vert _{2,1}$, we have

$$\begin{aligned} \langle \mathbf P ^{k+1}-\mathbf P ^{*}, \mathbf Z ^{k+1}-\mathbf Z ^{*}\rangle = D_{\Vert \cdot \Vert _{2,1}}^\mathbf{P ^k}(\mathbf Z ^k,\mathbf Z ^*) + D_{\Vert \cdot \Vert _{2,1}}^\mathbf{P ^*}(\mathbf Z ^*,\mathbf Z ^k). \end{aligned}$$

(71)

(71) and (70) imply that $\lim _{k\rightarrow + \infty } D_{\Vert \cdot \Vert _{2,1}}^\mathbf{P ^*}(\mathbf Z ^k,\mathbf Z ^*) + D_{\Vert \cdot \Vert _{2,1}}^\mathbf{P ^k}(\mathbf Z ^*,\mathbf Z ^k) =0$, and together with the nonnegativity of the Bregman distance, implies that

$$\begin{aligned} \lim _{k\rightarrow + \infty } D_{\Vert \cdot \Vert _{2,1}}^\mathbf{P ^*}(\mathbf Z ^k,\mathbf Z ^*) =0, \end{aligned}$$

(72)

i.e.,

$$\begin{aligned} \lim _{k\rightarrow + \infty } \Vert \mathbf Z ^k \Vert _{2,1} - \Vert \mathbf Z ^* \Vert _{2,1} - \langle \mathbf Z ^{k}-\mathbf Z ^{*}, \mathbf P ^{*} \rangle = 0. \end{aligned}$$

(73)

Moreover, since $\mu >0$, (67) also leads to $\sum _{k=0}^{+ \infty } \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 < + \infty$, which implies that $\lim _{k\rightarrow + \infty } \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 = 0$. By $\mathbf X ^{*} = \mathbf Z ^{*}$, we conclude that

$$\begin{aligned} \lim _{k\rightarrow + \infty } \Vert \mathbf X _e^{k+1} - \mathbf Z _e^{k} \Vert _F^2 = \lim _{k\rightarrow + \infty } \Vert \mathbf X ^{k+1} - \mathbf X ^{*} - \mathbf Z ^{k} + \mathbf Z ^{*} \Vert _F^2 \!=\! \lim _{k\rightarrow \!+\! \infty } \Vert \mathbf X ^{k+1} - \mathbf Z ^{k} \Vert _F^2 = 0.\nonumber \\ \end{aligned}$$

(74)

Since $\Vert \cdot \Vert _{2,1}$ is continuous, by (73) and (74), for $\mathbf X$, we have

$$\begin{aligned} \lim _{k\rightarrow + \infty } \Vert \mathbf X ^k \Vert _{2,1} - \Vert \mathbf X ^* \Vert _{2,1} - \langle \mathbf X ^{k}-\mathbf X ^{*}, \mathbf P ^{*} \rangle = 0. \end{aligned}$$

(75)

Furthermore, since $\mathbf A \mathbf X ^k \rightarrow \mathbf Y$ and $\mathbf A \mathbf X ^* = \mathbf Y$, we have

$$\begin{aligned} \lim _{k\rightarrow + \infty } \langle \mathbf A \mathbf X ^{k} - \mathbf A \mathbf X ^{*}, \mathbf W ^{*} \rangle = 0. \end{aligned}$$

(76)

Summing (75) and (76), it yields

$$\begin{aligned}&0 = \lim _{k\rightarrow + \infty } \Vert \mathbf X ^k \Vert _{2,1} - \Vert \mathbf X ^* \Vert _{2,1} - \langle \mathbf X ^{k} - \mathbf X ^{*}, \mathbf P ^{*} \rangle - \langle \mathbf A \mathbf X ^{k} - \mathbf A \mathbf X ^{*}, \mathbf W ^{*} \rangle \nonumber \\&\quad = \lim _{k\rightarrow + \infty } \Vert \mathbf X ^k \Vert _{2,1} - \Vert \mathbf X ^* \Vert _{2,1} - \langle \mathbf X ^{k} - \mathbf X ^{*}, \mathbf P ^{*}+\mathbf A ^T\mathbf W ^{*} \rangle \nonumber \\&\quad = \lim _{k\rightarrow + \infty } \Vert \mathbf X ^k \Vert _{2,1} - \Vert \mathbf X ^* \Vert _{2,1}, \end{aligned}$$

(77)

where the last equality comes from the first equation of (63). This is the second equation of (31).

Next, we prove (32) whenever (2) has a unique solution. It is proved by contradiction.

Let $\mathbf W ^*$ be the vector in (63). Define

$$\begin{aligned} \varPhi (\mathbf X ) = L(\mathbf X ,\mathbf W ^*) + \Vert \mathbf{AX-Y }\Vert _F^2 = \Vert \mathbf X \Vert _{2,1} + \langle \mathbf W ^*, \mathbf{AX-Y }\rangle + \Vert \mathbf{AX-Y }\Vert _F^2. \end{aligned}$$

(78)

(78) is convex and continuous. Since $(\mathbf X ^*,\mathbf W ^*)$ is a saddle point of $L(\mathbf X ,\mathbf W )$ and $\mathbf A \mathbf X ^*=\mathbf Y$, we have $\varPhi (\mathbf X ) \ge \varPhi (\mathbf X ^*)$. Especially, we have $\varPhi (\mathbf X ) > \varPhi (\mathbf X ^*)$ for $\mathbf X \ne \mathbf X ^*$. The above conclusion can be seen as follows: When $\mathbf X \ne \mathbf X ^*$, if $\mathbf A \mathbf X =\mathbf Y$, then $\varPhi (\mathbf X ) > \varPhi (\mathbf X ^*)$ holds immediately due to the uniqueness of the solution of (2); otherwise, $\Vert \mathbf{AX-Y }\Vert _F^2 > 0 = \Vert \mathbf A \mathbf X ^*-\mathbf Y \Vert _F^2$ and therefore

$$\begin{aligned}&\varPhi (\mathbf X ) = L(\mathbf X ,\mathbf W ^*) + \Vert \mathbf{AX-Y }\Vert _F^2 \ge L(\mathbf X ^*,\mathbf W ^*) + \Vert \mathbf{AX-Y }\Vert _F^2 \nonumber \\&> L(\mathbf X ^*,\mathbf W ^*) + \Vert \mathbf A \mathbf X ^*-\mathbf Y \Vert _F^2 = \varPhi (\mathbf X ^*). \end{aligned}$$

(79)

The remainder of the proof can follows the same line as the one in Theorem 1. $\square$

Appendix 3: Subgradient of $\Vert \mathbf X \Vert _{2,1}$

For $\Vert \mathbf X \Vert _{2,1} = \sum _{j=1}^n \Vert \mathbf X ^j \Vert _{2}$, the subgradient of $\Vert \mathbf X \Vert _{2,1}$ is obtained as

$$\begin{aligned} \frac{ \partial \Vert \mathbf X \Vert _{2,1} }{\partial \mathbf X } =\begin{bmatrix} \frac{ \partial \Vert \mathbf X ^1 \Vert _{2}}{\partial \mathbf X _{11}}&\cdots&\frac{ \partial \Vert \mathbf X ^1 \Vert _{2}}{\partial \mathbf X _{1L}} \\ \vdots&\ddots&\vdots \\ \frac{ \partial \Vert \mathbf X ^n \Vert _{2}}{\partial \mathbf X _{n1}}&\cdots&\frac{ \partial \Vert \mathbf X ^n \Vert _{2}}{\partial \mathbf X _{nL}} \end{bmatrix} =\begin{bmatrix} \frac{ \partial \Vert \mathbf X ^1 \Vert _{2}}{\partial \mathbf X ^{1}} \\ \vdots \\ \frac{ \partial \Vert \mathbf X ^n \Vert _{2}}{\partial \mathbf X ^{n}} \end{bmatrix} , \end{aligned}$$

(80)

where

$$\begin{aligned} \frac{ \partial \Vert \mathbf X ^j \Vert _{2}}{\partial \mathbf X ^{j}} =\left\{ \begin{array}{l@{\quad }l} \mathbf X ^j / \Vert \mathbf X ^j\Vert _2 &{} \text {if} \; \mathbf X ^j \ne \mathbf 0 , \\ \{ \mathbf v \big | \Vert \mathbf v \Vert _2 \le 1, \mathbf v \in \mathbb R ^{L}\} &{} \text {if} \; \mathbf X ^j = \mathbf 0 . \end{array} \right. \end{aligned}$$

(81)