High spectral quality pansharpening approach based on MTF-matched filter banks

Abstract

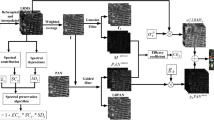
Pansharpening consists in merging a low-resolution multispectral image (MS) with a high spatial resolution panchromatic image (PAN) to produce a high resolution pansharpened MS image. It consists in enhancing spatially the low-resolution MS image by injecting the missing details provided by the high-resolution PAN image. In this paper, we propose a novel pansharpening approach based on decomposition/reconstruction processing using low-pass and high-pass filter banks. On the one hand, the low-pass approximation (taking into account the imaging system modulation transfer function MTF) of the pansharpened MS image is assumed to be equal to the original MS image in order to preserve the spectral quality. On the other hand, the high-pass filter allowing us to extract the high-frequency PAN details is designed as complementary filter to the low-pass one in order to provide perfect reconstruction in the ideal case. Quantitative assessment performed on reduced and full-resolution images are used to validate the proposed technique and compare it to state-of-art. Experimental results using Pléaides and GeoEye-1 data show that our proposed fusion schema outperforms the pre-existing methods visually as well as quantitatively.

Appendices

Appendix 1: Downsampling/upsampling processes

This appendix contains the equations defining the downsampling and upsampling processes.

For downsampling, a considered discrete input sequence x[n] having z-transform noted X(z) is subsampled by an integer factor M yielding to the output y[n] . The latter is obtained by discarding those samples of x[n] whose indices are not multiple of the integer M :

$$\begin{aligned} y[n] = \left\{ \begin{aligned} x[M n]&\quad \text {if } M \text { is even,}\\ 0&\quad \text {otherwise.}\\ \end{aligned} \right. \end{aligned}$$

(27)

The z -transform of y[n] is Y(z) given by:

$$\begin{aligned} Y(z) = \frac{1}{2} \left[ X(z^{\frac{1}{2}}) + X(-z^{\frac{1}{2}})\right] . \end{aligned}$$

(28)

where, the term $X(z^{\frac{1}{2}})$ is the expanded version of X(z) and the second term $X(-z^{\frac{1}{2}})$ is a shifted version of the first term. The term $X(-z^{\frac{1}{2}})$ causes an overlap in the frequency domain, which induces the aliasing effect. When aliasing occurs, the original signal, x[n], cannot be recovered perfectly from y[n] . To overcome this problem, the input signal should be bandlimited using a low-pass filtering. Therefore, ideal decimator is recommended before performing downsampling (Oppenheim and Schafer 2009).

Interpolating by a factor L consists in inserting $L-1$ ( L is an integer) zeros between successive samples. It is expressed by:

$$\begin{aligned} y[n] = \left\{ \begin{aligned} x \left[ \frac{n}{L} \right]&\quad \text {if }\frac{n}{L} \in \mathbb {Z} ,\\ 0&\quad \text {otherwise.}\\ \end{aligned} \right. \end{aligned}$$

(29)

The z -transform of the upsampled signal is:

$$\begin{aligned} Y(z) = X(z^{L}). \end{aligned}$$

(30)

The term Y(z) contains $L-1$ replica of the original spectrum, that causes spectral periodization effects. This phenomenon may be seen as the dual of the aliasing effect. In practice, in order to eliminate the replica produced by the upsampler, one may introduce a filtering step after the upsampling process.

Aliasing and spectral periodization may simultaneously occur, when downsamplers and upsamplers are cascaded (Vaidyanathan 1990). In this case, it is not possible to restore the input signal from its downsampled and upsampled version. Such distortions should be canceled (or at least reduced): the signal x[n] is filtered using low-pass filtering followed by a decimator, then it is interpolated and filtered by an ideal filter aiming at rejecting the spectral periodizations and retaining only the desired signal.

Appendix 2: Two-channel filter banks

Remark Let the z -transform of a sequence x[n] be X(z) .

The analysis filter bank (Fig. 1) decomposes the input signal x[n] into low and high frequency components $x_1[n]$ and $x_2[n]$, respectively, which are expressed as functions of X(z) by:

$$\begin{aligned} \left\{ \begin{aligned} X_1(z)= & {} H(z).X(z), \\ X_2(z)= & {} G(z).X(z). \end{aligned} \right. \end{aligned}$$

(31)

Then, the signals $x_1[n]$ and $x_2[n]$ in both channels are subsampled by a factor two according to [cf. (28), (31)]:

$$\begin{aligned} \left\{ \begin{aligned} V_1(z)= & {} \frac{1}{2} \left[ H(z^{1/2}).X(z^{1/2}) + H(-z^{1/2}). X(-z^{1/2})\right] ,\\ V_2(z)= & {} \frac{1}{2} \left[ G(z^{1/2}).X(z^{1/2}) + G(-z^{1/2}). X(-z^{1/2})\right] . \end{aligned} \right. \end{aligned}$$

(32)

The second configuration aims at reconstructing the original signal from the two smoothed and subsampled signals $v_1[n]$ and $v_2[n]$. These latter are upsampled by a factor two. Based on (30) and (32), the two components $U_1(z)$ and $U_2(z)$ are given by:

$$\begin{aligned} \left\{ \begin{aligned} U_1(z) = \frac{1}{2} [ H(z).X(z) + H(-z). X(-z)],\\ U_2(z) = \frac{1}{2} [ G(z).X(z) + G(-z). X(-z)]. \end{aligned} \right. \end{aligned}$$

(33)

Then, they are interpolated using low-pass and high-pass filtering: $h_r[n]$ and $g_r[n]$, respectively, obtaining the following components $Y_1(z)$ and $Y_2(z)$:

$$\begin{aligned} \left\{ \begin{aligned} Y_1(z) = H_r(z)U_1(z) = \frac{1}{2} H_r(z)[H(z)X(z)+H(-z)X(-z)],\\ Y_2(z) = G_r(z)U_2(z) = \frac{1}{2} G_r(z)[G(z)X(z)+G(-z)X(-z)]. \end{aligned} \right. \end{aligned}$$

(34)

Finally, the two components $Y_1(z)$ and $Y_2(z)$ are summed allowing the reconstruction of the output signal $x_r[n]$:

$$\begin{aligned} X_r(z) = \frac{1}{2}\lbrace \underbrace{ [H(z)H_r(z)+G(z)G_r(z)]}_{E(z)} X(z) + \underbrace{[H(-z)H_r(z)+G(-z)G_r(z)]}_{F(z)} X(-z)\rbrace , \end{aligned}$$

(35)

where E(z) and F(z) are called distortion transfer function and aliasing transfer function (Vetterli and Kovačević 1995), respectively.

In (35), the component involving X(z) represents the desired signal, whereas the term involving $X(-z)$ is the unwanted aliased component caused by downsampling that must be minimized.

Appendix 3: 4-reduction versus 2 -reduction Gaussian filters

For many remote sensing imaging systems, the resolution-scale between PAN and MS images is four. In order to downsample directly the PAN image to reach the resolution of MS image and to take into account the MTF of the MS sensors, the 4 -reduction filter ($r_4$) is used in this case. To respect the MTF Gaussian shape, Kallel (2015) defined it as a centered Gaussian distribution of standard deviation, $\sigma _4$, given by:

$$\begin{aligned} \sigma _4 = \frac{4}{\pi } \sqrt{\log (\alpha _{cf}^{-2})} \end{aligned}$$

(36)

where $\alpha _{cf}$ is the cutoff value at the Nyquist frequency.

Now, in our study, the two-channel filter bank is considered, the scale-ratio is equal two. The downsampling operation must be then applied twice. It consists of applying low-pass filter ($r_2$) followed by sub-sampling ($\downarrow 2$).

The question is how to compute the adequate filter $r_2$ such that when 2 -reduction downsampling is applied twice it fits the 4 -reduction one. At the one hand, according to Kallel (2015), the first level ( 2 -reduction) and the second level ( 4 -reduction) filters (respectively, $r_2$ and $r_4$ ) are linked together as follows:

$$\begin{aligned} r_{4}[n] = \sum _k r_{2}[k] r_{2}[n-2k] \end{aligned}$$

(37)

At the other hand, to conserve the radiometric properties, a reduction filter, r , must verify the averaging filter equality:

$$\begin{aligned} \sum _i {r}[i] = 1. \end{aligned}$$

(38)

Using the latter two equalities, we will show in the following that $r_2$ can be Gaussian-shaped.

Lemma 1

Let us consider the couple of filters (h, g) , satisfying the averaging property. Then, the filter v defined by:

$$\begin{aligned} v[n] = \sum _i h[i] g[n- 2 i]. \end{aligned}$$

(39)

satisfies it, too.

Proof

Summing all coefficients of the filter v :

$$\begin{aligned} \sum _n v[n] = \sum _n \sum _i h[i] g[n- 2 i] = \sum _i h[i] \sum _n g[n- 2 i] \end{aligned}$$

(40)

Then, substitute p for $n - 2 i$ in (40):

$$\begin{aligned} \sum _p v[p] = \sum _i h[i] \sum _p g[p] = 1 . \end{aligned}$$

(41)

$\square$

Theorem 1

Given a Gaussian filter, $v_2$, of standard deviation $\sigma$, defined by:

$$\begin{aligned} v_2[n] = a_{\sigma } \exp \left( \frac{- n^2 }{2 \sigma ^2} \right) , \end{aligned}$$

(42)

where $a_{\sigma }$ allows to verify the averaging property, i.e.:

$$\begin{aligned} a_{\sigma } = \frac{1}{\sum _n \exp \left( \frac{- n^2}{2 \sigma ^2}\right) } \end{aligned}$$

(43)

Then, the filter $v_4$ defined by:

$$\begin{aligned} v_{4}[n] = \sum _k v_{2}[k] v_{2}[n-2k] \end{aligned}$$

(44)

is a Gaussian filter of standard deviation $\sqrt{5} \sigma$.

Proof

(44) can be written as follows:

$$\begin{aligned} \begin{aligned} v_4[n]&= \sum _k a_{\sigma }^2 \exp \left( \frac{- k^2 }{2 \sigma ^2}\right) \exp \left( \frac{- (n-2k)^2 }{2 \sigma ^2}\right) \\&= a_{\sigma }^2 \sum _k \exp \left( \frac{- k^2}{2\sigma ^2}\right) \exp \left( \frac{- (n^2 - 4 n k + 4 k^2) }{2 \sigma ^2}\right) \\&= a_{\sigma }^2 \sum _k \exp \left( \frac{-5 k^2 + 4 n k - n^2}{2 \sigma ^2}\right) \\&= a_{\sigma }^2 \sum _k \exp \left( \frac{\frac{-n^2}{5} - \left( -\sqrt{5} k + \frac{2 n}{\sqrt{5}}\right) ^2}{2 \sigma ^2}\right) \\&= a_{\sigma }^2 \sum _k \exp \left( \frac{- n^2 }{10 \sigma ^2}\right) \exp \left( \frac{-\left( -\sqrt{5} k + \frac{2n}{\sqrt{5}}\right) ^2}{2 \sigma ^2}\right) \\&= a_{\sigma }^2 \exp \left( \frac{-n^2}{10\sigma ^2}\right) \sum _k \exp \left( \frac{-\left( -\sqrt{5} k + \frac{2 n}{\sqrt{5}}\right) ^2}{2 \sigma ^2}\right) \\&= a_{\sigma }^2 \exp \left( \frac{-n^2}{10\sigma ^2}\right) \sum _k\exp \left( \frac{-5}{2 \sigma ^2}\left( \frac{2n}{5}-k\right) \right) ^2 \\ \end{aligned} \end{aligned}$$

(45)

Then, replacing variable $\frac{2n}{5} -k$ by p, (45) can be written as:

$$\begin{aligned} v_4[n] = \left[ a_{\sigma }^2 \sum _{p} \exp \left( \frac{-5 p^2}{2 \sigma ^2}\right) \right] \exp \left( \frac{- n^2 }{10 \sigma ^2}\right) \end{aligned}$$

(46)

It is clear that $a_{\sigma }^2 \sum _p \exp \left( \frac{-5 p^2}{2 \sigma ^2}\right)$ is a constant. Moreover, according to Lemma 1, $v_4$ satisfies the averaging property, therefore:

$$\begin{aligned} a_{\sigma }^2 \sum _p \exp \left( \frac{-5 p^2}{2 \sigma ^2}\right) = \frac{1}{\sum \limits _{p} \exp \left( \frac{- p^2 }{10 \sigma ^2}\right) } \end{aligned}$$

(47)

Replacing (47) in (46), one find:

$$\begin{aligned} v_4 [n] = \frac{\exp \left( \frac{- n^2 }{10 \sigma ^2}\right) }{\sum \limits _p \exp \left( \frac{- p^2 }{10 \sigma ^2}\right) } \end{aligned}$$

(48)

Finally, it is possible to conclude that $v_{4}$ is a Gaussian distribution with a standard deviation equal $\sqrt{5} \sigma$. $\square$

According to Theorem 1, applying twice a Gaussian 2 -reduction downsampling of sdv $\sigma$ is equivalent to apply a Gaussian 4 -reduction filter of sdv $\sqrt{5} \sigma$. Now, in our case, we need to find $r_2$ such as $r_4$ is Gaussian of sdv $\sigma _4$. Therefore, $r_2$ can be chosen Gaussian of sdv $\sigma = \frac{\sigma _4}{\sqrt{5}}$.