DOA estimation with a rotational uniform linear array (RULA) and unknown spatial noise covariance

Abstract

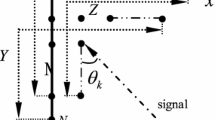
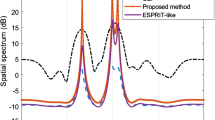
Direction of Arrival (DOA) estimation is one of the major tasks in array signal processing. In this paper, a new DOA estimation method is proposed using a rotational uniform linear array (RULA) consisting of omnidirectional sensors. The main contribution of the proposed method is that the number of distinguishable signals is larger than the methods in the literature with a uniform linear array consisting of the same number of omnidirectional sensors. Moreover, the new method can effectively reduce unknown spatial noises using a generalized complement projection matrix under the RULA framework. Simulations are presented to illustrate the effectiveness of the proposed method and comparison with some existing DOA estimation methods is also made.

Appendix

1.1 Proof of Proposition 1

An array contains at least 2 elements. For the number of elements $N \ge 2$, we have $N^2 > 2N-1$. The number of rows in $\mathbf {G}$ is larger than the number of columns and $\mathbf {G}$ is of full column rank. To complete the matrix, we construct a full column rank matrix $\mathbf {F} \in \mathbb {R}^{N^2 \times (N-1)^2}$, where each column in $\mathbf {F}$ is linearly independent of the columns in $\mathbf {G}$. Note that $2N-1+(N-1)^2$ is equal to $N^2$. Put two block matrices $\mathbf {F}$ and $\mathbf {G}$ together to form a new matrix $\mathbf {H} = \left[ \mathbf {F} \ \mathbf {G}\right] \in \mathbb {R}^{N^2 \times N^2}$. It is easy to see that $\mathbf {H}$ is of full rank $N^2$. Now construct $\widetilde{\mathbf {H}} = \mathrm{diag}\left\{ \mathbf {H}, \mathbf {H}, \ldots , \mathbf {H}\right\} \in \mathbb {R}^{N_\varphi N^2 \times N_\varphi N^2}$, where $\mathbf {H}$ appears $N_\varphi$ times as a block diagonal element in $\widetilde{\mathbf {H}}$. It is of full rank $N_\varphi N^2$. Next we can prove that $\mathbf {P}^\perp \widetilde{\mathbf {H}}$ is of rank $(N_\varphi -1)N^2$. To show this, we add the first block row of $\widetilde{\mathbf {H}}$ to every other block rows and get $\widetilde{\mathbf {H}}' = \begin{bmatrix} \mathbf {H}&\mathbf {0}&\cdots&\mathbf {0} \\ \mathbf {H}&\mathbf {H}&\cdots&\mathbf {0} \\ \vdots&\vdots&\vdots&\vdots \\ \mathbf {H}&\mathbf {0}&\cdots&\mathbf {H}\\ \end{bmatrix}$.

After multiplication with $\mathbf {P}^\perp$, the first $N^2$ columns of $\widetilde{\mathbf {H}}'$ will vanish. Thus the rank of $\mathbf {P}^\perp \widetilde{\mathbf {H}}'$ is smaller than or equal to $(N_\varphi -1) N^2$. At the same time, we notice that $\mathbf {P}^\perp$ can eliminate at most $N^2$ columns. So the rank of $\mathbf {P}^\perp \widetilde{\mathbf {H}}'$ is larger than or equal to $(N_\varphi -1) N^2$. Putting them together, we conclude that the rank of $\mathbf {P}^\perp \widetilde{\mathbf {H}}'$ is equal to $(N_\varphi -1) N^2$. Therefore, the rank of $\mathbf {P}^\perp \widetilde{\mathbf {H}}$ is also equal to $(N_\varphi -1) N^2$. It means exactly $N^2$ columns in $\widetilde{\mathbf {H}}$ are eliminated. Among them, $(N-1)^2$ of them are linear combinations of the columns in $\mathrm{diag}\left\{ \mathbf {F}, \mathbf {F}, \ldots , \mathbf {F}\right\} \in \mathbb {R}^{N_\varphi N^2 \times N_\varphi (N-1)^2}$. Those columns are linearly independent of the columns in $\widetilde{\mathbf {G}}$. Therefore, $\mathbf {P}^\perp$ will eliminate exactly $2N-1$ columns of the linear combinations of columns in $\widetilde{\mathbf {G}}$. As a result, $\mathbf {P}^\perp \widetilde{\mathbf {G}}$ is of rank $N_\varphi (2N-1) -(2N-1)=(N_\varphi -1)(2N-1)$.