Skip to main content

Advertisement

Springer Nature Link
Log in

Convergent method for designing high-accuracy bi-equiripple variable-delay filters using new delay-error expression

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

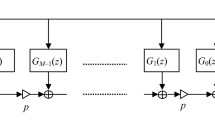
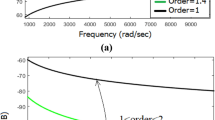
This paper proposes a fast non-iterative approach to the design of an odd-order bi-equiripple variable-delay (VD) digital filter whose mathematical model is a multi-variable (MV) transfer function. The objective of the bi-equiripple design is to minimize the maximum frequency-response deviation of this MV transfer function while mitigating the large overshoots of the VD response at the same time. Since the group-delay function is nonlinear with respect to the MV transfer-function coefficients, it is first linearized through using an approximate approach. This linearization enables the bi-equiripple VD filter to be designed with linear constraints, and the bi-equiripple design is then formulated as a convex minimization problem. The convex minimization does not require any iterations and thus it is fast and yields a convergent optimal solution. Solving the convex minimization problem produces a bi-equiripple VD filter with minimized worst-case frequency-response error and mitigated VD-deviation overshoots (jumps). An illustrating example is presented to demonstrate the above simultaneous deviation suppressions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  • Deng, T.-B. (2001). Discretization-free design of variable fractional-delay FIR digital filters. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 48(6), 637–644.

    Article  Google Scholar 

  • Deng, T.-B. (2004). Closed-form design and efficient implementation of variable digital filters with simultaneously tunable magnitude and fractional-delay. IEEE Transactions on Signal Processing, 52(6), 1668–1681.

    Article  MathSciNet  MATH  Google Scholar 

  • Deng, T.-B. (2007). Symmetric structures for odd-order maximally flat and weighted-least-squares variable fractional-delay filters. IEEE Transactions on Circuits and Systems I: Regular Papers, 54(12), 2718–2732.

    Article  Google Scholar 

  • Deng, T.-B. (2011). Minimax design of low-complexity even-order variable fractional-delay filters using second-order cone programming. IEEE Transactions on Circuits and Systems II: Express Briefs, 58(10), 692–696.

    Article  Google Scholar 

  • Deng, T.-B. (2012a). Bi-minimax design of odd-order variable fractional-delay digital filters. In Proceedings of IEEE ISCAS 2012 (pp. 786–789) Seoul, Korea.

  • Deng, T.-B. (2012b). Low-complexity and high-accuracy odd-order variable fractional-delay digital filters. In Proceedings of IEEE ICASSP 2012 (pp. 1589–1592). Kyoto, Japan.

  • Deng, T.-B., Chivapreecha, S., & Dejhan, K. (2012). Bi-minimax design of even-order variable fractional-delay FIR digital filters. IEEE Transactions on Circuits and Systems I: Regular Papers, 59(8), 1766–1774.

    Article  MathSciNet  Google Scholar 

  • Deng, T.-B., & Lian, Y. (2006). Weighted-least-squares design of variable fractional-delay FIR filters using coefficient-symmetry. IEEE Transactions on Signal Processing, 54(8), 3023–3038.

    Article  MATH  Google Scholar 

  • Deng, T.-B., & Qin, W. (2013). Coefficient relation-based minimax design and low-complexity structure of variable fractional-delay digital filters. Signal Processing, 93(4), 923–932.

    Article  Google Scholar 

  • Deng, T.-B., & Qin, W. (2014). Improved bi-equiripple variable fractional-delay filters. Signal Processing, 94(1), 300–307.

    Article  Google Scholar 

  • Deng, T.-B., & Soontornwong, P. (2016). Delay-error-constrained minimax design of all-pass variable-fractional-delay digital filters. Signal Processing, 120(3), 438–447.

    Article  Google Scholar 

  • Farrow, C. W. (1988). A continuously variable digital delay element. In Proceedings of IEEE ISCAS 1988 (Vol. 3, pp. 2641–2645). Espoo, Finland.

  • Liu, G.-S., & Wei, C.-W. (1992). A new variable fractional sample delay filter with nonlinear interpolation. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 39(2), 123–126.

    Article  Google Scholar 

  • Liu, J.-C., & You, S.-J. (2007). Weighted least squares near-equiripple approximation of variable fractional delay FIR filters. IET Signal Processing, 1(2), 66–72.

    Article  Google Scholar 

  • Pei, S.-C., Shyu, J.-J., Huang, Y.-D., & Chan, C.-H. (2012). Improved methods for the design of variable fractional-delay IIR digital filters. IEEE Transactions on Circuits and Systems I: Regular Papers, 59(5), 989–1000.

    Article  MathSciNet  Google Scholar 

  • Soontornwong, P., & Chivapreecha, S. (2015). Pascal-interpolation-based noninteger delay filter and low-complexity realization. Radioengineering, 24(4), 1002–1012.

    Article  Google Scholar 

  • Tseng, C.-C., & Lee, S.-L. (2012). Design of fractional delay filter using Hermite interpolation method. IEEE Transactions on Circuits and Systems I: Regular Papers, 59(7), 1458–1471.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Information Science, Faculty of Science, Toho University, Miyama 2-2-1, Funabashi, Chiba, 274-8510, Japan

    Tian-Bo Deng

Authors
  1. Tian-Bo Deng
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Tian-Bo Deng.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Deng, TB. Convergent method for designing high-accuracy bi-equiripple variable-delay filters using new delay-error expression. Multidim Syst Sign Process 30, 343–361 (2019). https://doi.org/10.1007/s11045-018-0559-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11045-018-0559-3

Keywords