Non-iterative CS recovery algorithm for surveillance applications: subjective and real-time experience

Abstract

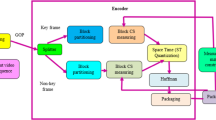
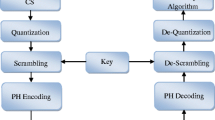
Non-iterative compressed sensing (CS) based recovery algorithms have been proposed in the recent years that efficiently recover the input from CS measurements without iterations. When it comes to reconstruction of images and videos for medical, military and surveillance applications, faster computations accompanied by least complexity and high accuracy is mandatory. Such large volumes of data can be effectively handled by non-iterative pseudo inverse based recovery algorithm (NIPIRA). This study uses NIPIRA to reconstruct the surveillance videos from the CS measurements and the algorithm’s efficiency is measured in terms of subjective measure and hardware implementation. The average peak signal to noise ratio exhibited by NIPIRA is around 32 dB; the mean opinion score is 3.5 that corresponds to ‘Fair’ quality reconstruction. Hardware implementation proves that NIPIRA recovers videos within seconds compared to iterative ones that take hours for the same. The upshot is that NIPIRA is perfectly suitable for surveillance applications.

Appendix

Apart from the experimental results, NIPIRA exhibits less error. This is because the sparse augmented matrix introduced in order to capture the measurements avoids the presence of spurious data and selects only the necessary information. Hence the optimum error cause by the logarithm is less than the additive or combined error. This is mathematically proved by the following derivation.

Optimality of NIPIRA This subsection mathematically supports the algorithmic procedure of NIPIRA with the proof for optimality of the algorithm. To prove the same, it is necessary to prove that the error between the input and reconstructed vectors $\Vert x-\varPhi ^{\dagger } y\Vert _{2}$ is dependent on the difference terms $\Vert x-x_{s}\Vert _{2}$, $\dfrac{\Vert x-x_{s}\Vert _{1}}{\sqrt{s}}$ and $\Vert e\Vert _{2}$ (Florence Gnana Poovathy and Radha 2016). The estimate that would reconstruct the best approximation is denoted as $\varPhi ^{\dagger } y$, where $\dagger$ signifies the pseudo inverse. $\Vert x-\varPhi ^{\dagger } y\Vert _{2}$ can be represented in terms of $\Vert x-x_{s}\Vert _{2}$ and $\Vert e\Vert _{2}$ as follows:

$$\begin{aligned} \Vert x-\varPhi ^{\dagger } y\Vert _{2}=\Vert x-x_{s}-\varPhi ^{\dagger } \varPhi (x-x_{s})-\varPhi ^{\dagger } e\Vert _{2} \end{aligned}$$

(4)

This can be combined as,

$$\begin{aligned} \Vert x-\varPhi ^{\dagger } y\Vert _{2}= & {} \Vert x-x_{s}\Vert _{2}+\Vert \varPhi ^{\dagger } \varPhi (x-x_{s})\Vert _{2}+\Vert \varPhi ^{\dagger } e\Vert _{2} \end{aligned}$$

(5)

$$\begin{aligned} \Vert x-\varPhi ^{\dagger } y\Vert _{2}= & {} \Vert x-x_{s}\Vert _{2}+\Vert \varPhi ^{\dagger }\Vert _{2} \Vert \varPhi (x-x_{s})\Vert _{2}+\Vert \varPhi ^{\dagger }\Vert _{2} \Vert e\Vert _{2} \end{aligned}$$

(6)

For general CS recovery process, a common lemma (Candes et al. 2006) is available which states that

$$\begin{aligned} \Vert \varPhi x\Vert _{2}\le \sqrt{1+\delta _{s}}\Vert x\Vert _{2}+\sqrt{1+\delta _{s}}\dfrac{\Vert x\Vert _{1}}{\sqrt{s}} \end{aligned}$$

(7)

Therefore,

$$\begin{aligned} \Vert \varPhi (x-x_{s})\Vert _{2}\le \sqrt{1+\delta _{s}}\Vert (x-x_{s})\Vert _{2}+\sqrt{1+\delta _{s}}\dfrac{\Vert (x-x_{s})\Vert _{1}}{\sqrt{s}} \end{aligned}$$

(8)

and

$$\begin{aligned} \Vert \varPhi \Vert _{2}=\dfrac{1}{\sqrt{1-\delta _{s}}} \end{aligned}$$

(9)

Substituting Eqs. 8 and 9 in 6,

$$\begin{aligned} \Vert x-\varPhi ^{\dagger } y\Vert _{2}&\le \Vert x-x_{s}\Vert _{2}\dfrac{\sqrt{1+\delta _{s}}}{\sqrt{1-\delta _{s}}}\Vert x-x_{s}\Vert _{2} \nonumber \\&\quad +\dfrac{\sqrt{1+\delta _{s}}}{\sqrt{1-\delta _{s}}}\dfrac{\Vert x-x_{s}\Vert _{1}}{\sqrt{s}}+\dfrac{1}{\sqrt{1-\delta _{s}}}\Vert e\Vert _{2} \end{aligned}$$

(10)

Combining the like terms together,

$$\begin{aligned} \Vert x-\varPhi ^{\dagger } y\Vert _{2}&\le \left( 1+\dfrac{\sqrt{1+\delta _{s}}}{\sqrt{1-\delta _{s}}}\right) \Vert x-x_{s}\Vert _{2} \nonumber \\&\quad +\dfrac{\sqrt{1+\delta _{s}}}{\sqrt{1-\delta _{s}}}\dfrac{\Vert x-x_{s}\Vert _{1}}{\sqrt{s}}+\dfrac{1}{\sqrt{1-\delta _{s}}}\Vert e\Vert _{2} \end{aligned}$$

(11)

From Eq. 11, it is proved that, the optimum error exhibited by NIPIRA is less than the combined error term $\Vert x-x_{s}\Vert _{2}$ and $\Vert e\Vert _{2}$. Hence optimality in reconstruction is preserved perfectly by NIPIRA. Another important parameter that can define the perfection of an algorithm is accuracy. Taking surveillance videos as input, the accuracy in recovery is above 95%. This projects NIPIRA to be the best non-iterative algorithm for reconstruction of surveillance videos. The PSNR obtained using NIPIRA is averagely 30 dB for 31.25% of input information (i.e. $M=20$).