Skip to main content
Springer Nature Link
Log in

3-D modelling of rectangular circuits as the particular class of spatially interconnected systems on the plane

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

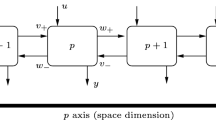
This paper is devoted to modelling the spatially interconnected system, particularly the regular circuit displayed in the plane as a 3-D system with two spatial indeterminates and one temporal indeterminate. First, the singular and nonsingular 3-D models of the Fornasini–Marchesini type are derived. Next, these models are transformed into the equivalent Roesser models. This work is a basis for further control applications of spatially interconnected systems on the plane.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Ahn, C. K., Shi, P., & Basin, M. V. (2015). Two-dimensional dissipative control and filtering for roesser model. IEEE Transactions on Automatic Control, 60(7), 1745–1759.

    MathSciNet  MATH  Google Scholar 

  • Antsaklis, P . J., & Michel, A . N. (2007). A linear systems primer (Vol. 1). Boston: Birkhäuser.

    MATH  Google Scholar 

  • Beck, C., & D’Andrea, R. (2004). Noncommuting multidimensional realization theory: Minimality, reachability, and observability. IEEE Transactions on Automatic Control, 49(10), 1815–1822.

    MathSciNet  MATH  Google Scholar 

  • Bose, N., Buchberger, B., & Guiver, J. (2003). Multidimensional systems theory and applications. Dordrecht: Kluwer.

    Google Scholar 

  • Bose, N. K. (1982). Applied multidimensional systems theory. New York: Van Nostrand Reinhold.

    MATH  Google Scholar 

  • Boudellioua, M. S. (2005). Equivalence to Smith form over a multivariate polynomial ring. In The fourth internatinal workshop on multidimensional systems (pp. 259–262).

  • Boudellioua, M. S., Galkowski, K., & Rogers, E. (2017). Equivalent 2-D nonsingular Roesser models for discrete linear repetitive processes. International Journal of Control, 1–9. https://doi.org/10.1080/00207179.2017.1414307

  • Chen, C. (1995). Linear system theory and design. Oxford: Oxford University Press, Inc.

    Google Scholar 

  • Cockburn, J. C. (2000). Multidimensional realizations of systems with parametric uncertainty. In Proceedings of MTNS (p. 6).

  • Cunha, D. P. (2013). Reduced order state-space models for 2-D systems. Master’s thesis, Dept. Elect. Comput. Eng., Univ. Porto, Portugal.

  • Ding, D.-W., Wang, H., & Li, X. (2015). \({H}_{-}/{H}_{\infty }\) fault detection observer design for two-dimensional roesser systems. Systems & Control Letters, 82, 115–120.

    MathSciNet  MATH  Google Scholar 

  • Dorf, R . C., & Bishop, R . H. (2011). Modern control systems. London: Pearson.

    MATH  Google Scholar 

  • Du, C., Xie, L., & Zhang, C. (2001). \({H}_\infty \) control and robust stabilization of two-dimensional systems in Roesser models. Automatica, 37(2), 205–211.

    MathSciNet  MATH  Google Scholar 

  • Feng, Z., & Xu, L. (2018). Optimization of coordinate transformation matrix for \({H}_\infty \) static-output-feedback control of 2-D discrete systems in FM second model. Multidimensional Systems and Signal Processing, 29(4), 1727–1737.

    MathSciNet  Google Scholar 

  • Feng, Z.-Y., Wu, Q., & Xu, L. (2012). \({H}_{\infty }\) control of linear multidimensional discrete systems. Multidimensional Systems and Signal Processing, 23(3), 381–411.

    MathSciNet  MATH  Google Scholar 

  • Fornasini, E., & Marchesini, G. (1976). State space realization theory of two-dimensional filters. IEEE Transactions on Automatic Control, 21(4), 484–492.

    MathSciNet  MATH  Google Scholar 

  • Friedland, B. (1986). Control systems design: An introduction to state-space methods. New York: McGraw-Hill.

    MATH  Google Scholar 

  • Galkowski, K. (2001). State space realization of linear 2-D systems with extensions to the general nD (\(n>2\)) case. London: Springer.

  • Kaczorek, T. (1985). Two-dimensional linear systems. London: Springer.

    MATH  Google Scholar 

  • Kaczorek, T. (1988). Singular models of 2-D systems. In Proceedings of the 12th World Congress on Scientific Computation, Paris (France).

  • Kailath, T. (1980). Linear systems. Upper Saddle River: Prentice-Hall.

    MATH  Google Scholar 

  • Lin, Z., & Bruton, L. (1989). BIBO stability of inverse 2-D digital filters in the presence of nonessential singularities of the second kind. IEEE Transactions on Circuits and Systems, 36(2), 244–254.

    MathSciNet  MATH  Google Scholar 

  • Lin, Z., Lam, J., Galkowski, K., & Xu, S. (2001). A constructive approach to stabilizability and stabilization of a class of nD systems. Multidimensional Systems and Signal Processing, 12(3–4), 329–343.

    MathSciNet  MATH  Google Scholar 

  • Lu, W.-S. (1995). On robust stability of 2-D discrete systems. IEEE Transactions on Automatic Control, 40(3), 502–506.

    MathSciNet  MATH  Google Scholar 

  • Magni, J.-F. (2006). User manual of the linear fractional representation toolbox version 2.0. Systems Control and Flight Dynamics Department. http://w3.onera.fr/smac/lfrt. Accessed 17 Mar 2014.

  • Paszke, W., Dabkowski, P., Rogers, E., & Gałkowski, K. (2015). New results on strong practical stability and stabilization of discrete linear repetitive processes. Systems & Control Letters, 77, 22–29.

    MathSciNet  MATH  Google Scholar 

  • Roesser, R. (1975). A discrete state-space model for linear image processing. IEEE Transactions on Automatic Control, 20(1), 1–10.

    MathSciNet  MATH  Google Scholar 

  • Rogers, E., Galkowski, K., & Owens, D. H. (2007). Control Systems theory and applications for linear repetitive processes. Control and information sciences. Berlin, Heidelberg: Springer.

    MATH  Google Scholar 

  • Sulikowski, B. (2018). Robust \({H}_2\) control of ladder circuits modeled as a subclass of \(2\)D systems. In Proceedings of the 17th annual European control conference (ECC2018) (pp. 888–893). Limassol, Cyprus.

  • Sulikowski, B., Galkowski, K., & Kummert, A. (2015). Proportional plus integral control of ladder circuits modeled in the form of two-dimensional (2D) systems. Multidimesional Systems and Signal Processing, 26(1), 267–290.

    MathSciNet  MATH  Google Scholar 

  • Wang, K., Chen, M. Z., & Chen, G. (2017). Realization of a transfer function as a passive two-port RC ladder network with a specified gain. International Journal of Circuit Theory and Applications, 45(11), 1467–1481.

    Google Scholar 

  • Xu, L., & Yan, S. (2010). A new elementary operation approach to multidimensional realization and LFR uncertainty modeling: The SISO case. Multidimensional Systems and Signal Processing, 21(4), 343–372.

    MathSciNet  MATH  Google Scholar 

  • Xu, L., Yan, S., Lin, Z., & Matsushita, S. (2012). A new elementary operation approach to multidimensional realization and LFR uncertainty modeling: The MIMO case. IEEE Transactions on Circuits and Systems-I, 59(3), 638–651.

    MathSciNet  Google Scholar 

  • Yan, S., Xu, L., Zhang, Y., Cai, Y., & Zhao, D. (2018). Order evaluation to new elementary operation approach for MIMO multidimensional systems. International Journal of Control, (just-accepted):1–20.

  • Yan, S., Xu, L., Zhao, Q., & Tian, Y. (2014). Elementary operation approach to order reduction for Roesser state-space model of multidimensional systems. IEEE Transactions on Circuits and Systems I: Regular Papers, 61(3), 789–802.

    Google Scholar 

  • Yan, S., Zhao, D., Xu, L., Cai, Y., & Li, Q. (2017). A novel elementary operation approach with Jordan transformation to order reduction for Roesser state-space model. Multidimensional Systems and Signal Processing, 28(4), 1417–1442.

    MathSciNet  MATH  Google Scholar 

  • Zerz, E. (1999). LFT representations of parametrized polynomial systems. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 46(3), 410–416.

    MathSciNet  MATH  Google Scholar 

  • Zerz, E. (2000). Topics in multidimensional linear systems theory. London: Springer.

    MATH  Google Scholar 

  • Zhao, D., Yan, S., Matsushita, S., & Xu, L. (2017). Order reduction for Roesser state-space model based on a certain system of equations. In 2017 10th international workshop on multidimensional (nD) systems (nDS) (pp. 1–5).

  • Zhao, D., Yan, S., & Xu, L. (2018). Eigenvalue trim approach to exact order reduction for Roesser state-space model of multidimensional systems. Multidimensional Systems and Signal Processing, 29(4), 1905–1934.

    MathSciNet  Google Scholar 

  • Zhou, K., Doyle, J . C., & Glover, K. (1996). Robust and optimal control (Vol. 40). New Jersey: Prentice hall.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Intelligent Mechatronics, Akita Prefectural University, Akita, 015-0055, Japan

    Dongdong Zhao & Li Xu

  2. Institute of Control and Computation Engineering, University of Zielona Gora, 65-516, Zielona Gora, Poland

    Krzysztof Galkowski & Bartlomiej Sulikowski

Authors
  1. Dongdong Zhao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Krzysztof Galkowski
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Bartlomiej Sulikowski
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Li Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dongdong Zhao.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work is partially supported by National Science Centre in Poland, Grant No. 2015/17/B/ST7/03703, the Japan Society for the Promotion of Science (JSPS.KAKENHI15K06072).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, D., Galkowski, K., Sulikowski, B. et al. 3-D modelling of rectangular circuits as the particular class of spatially interconnected systems on the plane. Multidim Syst Sign Process 30, 1583–1608 (2019). https://doi.org/10.1007/s11045-018-0619-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11045-018-0619-8

Keywords