Expanded coprime array for DOA estimation: augmented consecutive co-array and reduced mutual coupling

Abstract

Generalized coprime structure decomposes the interleaved subarrays in the conventional coprime array by introducing a displacement and the resulting CADiS, i.e. coprime array with displaced subarrays, configuration can enlarge the minimum adjacent spacing between elements to multiples of half-wavelength, which is considerably attractive in alleviating mutual coupling effect. However, the difference co-array that CADiS yields is fractured, which greatly deteriorates direction of arrival (DOA) estimation performance and achievable degrees of freedom of the algorithms based on consecutive co-array, e.g. spatial smoothing technique and Toeplitz matrix method. In this paper, from the mutual coupling effect and difference co-array perspective, we propose an expanded coprime array (ECA) structure by two steps. The first step is to further augment the displacement between the subarrays of CADiS to suppress the mutual coupling effect. The second step is to relocate a proper number of rightmost elements to concatenate the dominant consecutive co-array generated by CADiS to enhance the consecutive difference co-array. Specifically, we provide the closed-form expressions of resulting consecutive difference co-array, the number of relocated elements and their positions. Furthermore, different from the spatial smoothing based methods, we employ Toeplitz matrix property to directly construct the full-rank covariance matrix of the received data from the consecutive co-array with a lower computational cost and present the Toeplitz-MUSIC algorithm to testify the effectiveness and superiority of the proposed ECA structure.

Appendices

Appendix I

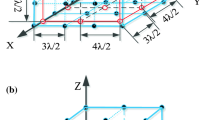
• (a) According to (13), the proposed structure is composed of three subarrays, which are specified by integer sets ${\mathbb{S}}_{1}$, ${\mathbb{S}}_{2}$ and ${\mathbb{S}}_{3}$, respectively. The difference co-array generated by ${\mathbb{S}}_{1}$ and ${\mathbb{S}}_{2}$ has holes distributed symmetrically on both positive and negative axis. When $R = \left\lfloor {M/2} \right\rfloor$, the position of holes on the positive axis can be specified by the following sets (Qin et al. 2015)

  $$ \left\{ {\begin{array}{*{20}l} {{\mathbb{H}}_{11} = \{ h_{11} |h_{11} = MN - aM - bN\} } \hfill \\ {{\mathbb{H}}_{12} = \{ h_{12} |h_{12} = M + dN\} } \hfill \\ {{\mathbb{H}}_{2} = \{ h_{2} |h_{2} = - (MN - aM - bN) + \delta \} } \hfill \\ \end{array} } \right. $$

  (a.1)

  where $a \in \left[ {1,\left\lfloor {N - N/M} \right\rfloor } \right] \subseteq [1,N - 2]$, $b \in \left[ {1,\left\lfloor {M - aM/N} \right\rfloor } \right] \subseteq [1,M - 1]$, $d \in [1,M]$ and $\delta = 3MN + M - (R + 1)N$, which denotes the virtual array aperture on the positive axis. Note that holes in ${\mathbb{H}}_{11}$ and ${\mathbb{H}}_{12}$ locate in the central part of the whole virtual array. The proof of (a.1) can be easily obtained using contradiction.

  Next, we prove that virtual sensors brought by ${\mathbb{S}}_{3}$ can fill all holes in the central part of difference co-array generated by ${\mathbb{S}}_{1}$ and ${\mathbb{S}}_{2}$, i.e., holes specified by ${\mathbb{H}}_{11}$ and ${\mathbb{H}}_{12}$.

  Holes in ${\mathbb{H}}_{11}$ can be rewritten as follows.

  For $b = 1$,

  $$ \begin{aligned} h_{11} & = MN - aM - N \\ & = (MN - N) - aM \\ \end{aligned} $$

  (a.2)

  For $b = b_{0} \in [2,R]$,

  $$ \begin{aligned} h_{11} & = MN - aM - b_{0} N \\ & = (MN - M - b_{0} N) - (a - 1)M \\ \end{aligned} $$

  (a.3)

  For $b = M - b_{0} \in [M - R,M - 2]$,

  $$ \begin{aligned} h_{11} & = MN - aM - (M - b_{0} )N \\ & = (N - a - 1)M - (MN - M - b_{0} N) \\ \end{aligned} $$

  (a.4)

  For $b = M - 1$,

  $$ \begin{aligned} h_{11} & = MN - aM - (M - 1)N \\ & {\kern 1pt} = (N - a)M - (MN - N) \\ \end{aligned} $$

  (a.5)

  Clearly, terms $MN - N$ and $MN - M - b_{0} N$ belongs to ${\mathbb{S}}_{3}$, while terms $aM$, $(a - 1)M$, $(N - a - 1)M$ and $(N - a)M$ belongs to ${\mathbb{S}}_{1}$, which means all holes in ${\mathbb{H}}_{11}$ can be filled by difference co-array generated by ${\mathbb{S}}_{1}$ and ${\mathbb{S}}_{3}$.

  Holes in ${\mathbb{H}}_{12}$ can be rewritten as follows.

  For $d = 1$,

  $$ \begin{aligned} h_{12} & = M + N \\ & = (MN - N) - (MN - M - 2N) \\ \end{aligned} $$

  (a.6)

  For $d \in [2,M]$,

  $$ \begin{aligned} h_{12} & = M + dN \\ & = \left[ {MN + M + N + (d - 2)N} \right] - (MN - N) \\ \end{aligned} $$

  (a.7)

  Clearly, terms $MN - N$ and $MN - M - 2N$ belongs to ${\mathbb{S}}_{3}$, while $MN + M + N + (d - 2)N \in {\mathbb{S}}_{2}$, which means all holes in ${\mathbb{H}}_{12}$ can be filled by difference co-array generated by ${\mathbb{S}}_{2}$ and ${\mathbb{S}}_{3}$. And hence we can conclude that all holes in the central part of difference co-array can filled when $R = \left\lfloor {M/2} \right\rfloor$.

• (b) Based on Qin et al. (2015), virtual sensors produced by ${\mathbb{S}}_{1}$ and ${\mathbb{S}}_{2}$ distribute consecutively in the range $\left[ {MN + M + 1,\;2MN + 2M - RN - 1} \right]$. According to the proof of property (a), the consecutive range on the positive axis can be enlarged to $[0,2MN + 2M - RN - 1]$. Besides, holes in ${\mathbb{H}}_{2}$ can be rewritten as

  $$ \begin{aligned} h_{2} & = - (MN - aM - bN) + \delta \\ & = \left[ {\left( {MN + M + N + mN} \right) - \left( {MN - M - cN} \right)} \right] \\ & \quad + \,\left( {a - 1} \right)M + \left( {2M - R + b - m - c - 2} \right)N \\ \end{aligned} $$

  (a.8)

  where $m \in [0,2M - R - 2]$, $c \in [2,R]$. When $a = 1$, $b \le R$, (a.8) can be further transformed into

  $$ h_{2} = \left( {MN + M + N + mN} \right) - \left( {MN - M - cN} \right) $$

  (a.9)

  where $MN + M + N + mN \in {\mathbb{S}}_{2}$, $MN - M - cN \in {\mathbb{S}}_{3}$, hence holes in ${\mathbb{H}}_{2}$ with $a = 1$, $b \le R$ can be filled by difference co-array generated by ${\mathbb{S}}_{2}$ and ${\mathbb{S}}_{3}$. Specifically, among the filled holes in ${\mathbb{H}}_{2}$, only the one with $a = 1$, $b = 1$ plays the role of enlarging the consecutive range after being filled since $M < N$. Therefore, it can be easily concluded that the difference co-array contains all the continuous integers in the range $[ - \,D,D]$, where $D = 2MN + 3M - RN - 1$ and the cDOF is $2D + 1$.

• (c) According to the proof of property (a), when $M$ is odd, holes in ${\mathbb{H}}_{11}$ are filled with unique sensor pairs presented in (a.2)–(a.5). On the contrary, when $M$ is even, holes with $b = R$ can be filled by both (a.3) and (a.4). Therefore, we can obtain the weight function as

  $$ \begin{aligned} & M\;{\text{is}}\;{\text{even:}}\quad w(l) = 1,\quad l \in [1,M - 1] \\ & M\;{\text{is}}\;{\text{odd:}}\quad w(l) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {l \in [1,M - 1]\;\& \;l \ne M/2} \hfill \\ {2,} \hfill & {l = M/2} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

Appendix II

In the case of IECA, the position of holes generated by ${\mathbb{S}}_{1}$ and ${\mathbb{S}}_{2}$ is still given by (a.1). Similarly, when $M \ge 6$ and $M$ is even, all holes in ${\mathbb{H}}_{11}$ and ${\mathbb{H}}_{12}$ can be filled by virtual sensors brought by ${\mathbb{S}}_{3}$. Besides, holes in ${\mathbb{H}}_{2}$ with $a = 1$, $b \le R - 1$ can be rewritten as

$$ \begin{aligned} h_{2} & = - (MN - aM - bN) + \delta \\ & = 2MN + 2M + (b - R - 1)N \\ & = (MN + M + N + mN) - (MN - M - cN) \\ \end{aligned} $$

(a.10)

where $m \in \left[ {0,2M - R - 2} \right]$, $c \in \left[ {2,R - 1} \right]$. Holes in ${\mathbb{H}}_{2}$ with $a = 2$, $b \le R$ can be rewritten as

$$ \begin{aligned} h_{2} & = - (MN - aM - bN) + \delta \\ & = 2MN + 3M + (b - R - 1)N \\ & = (MN + M + N + mN) - (MN - 2M - RN) \\ \end{aligned} $$

(a.11)

where $m \in \left[ {0,2M - R - 2} \right]$. Clearly, $MN + M + N + mN \in {\mathbb{S}}_{2}$, while terms $MN - M - cN$ and $MN - 2M - RN$ belongs to ${\mathbb{S}}_{3}$, which means holes in ${\mathbb{H}}_{2}$ with $a = 1$, $b \le R - 1$ and $a = 2$, $b \le R$ can be filled by difference co-array generated by ${\mathbb{S}}_{2}$ and ${\mathbb{S}}_{3}$. Besides, it is easy to observe that among these filled holes, holes with $(a,b) = (1,1)$, $(1,2)$ and $(2,1)$ can enlarge the consecutive range after being filled. Therefore, the resulting difference co-array contains all the continuous integers in the range $[ - \,D,D]$, where $D = 2MN + 4M - RN - 1$ and the cDOF is $2D + 1$.