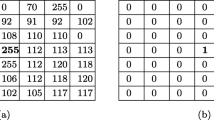
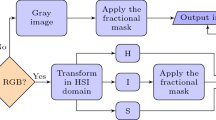
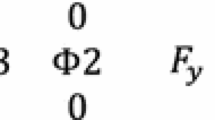Abstract
Digital images are affected by various types of noises, which may be incorporated into the image during its acquisition, transmission etc. Removal of these unwanted noises is an essential task, especially for digital images being used for various science, engineering, and biomedical applications. Depending upon the image acquisition process/devices, transmission medium, and other factors, noise present in digital images can be modeled into various types such as Gaussian noise, salt and paper noise etc. Most of the de-noising algorithms such as bilateral filter, Gaussian filter etc., perform well for Gaussian noise. However, these algorithms perform unsatisfactorily for impulsive noise, such as speckle noise. Aim of the proposed (research) work is to develop a de-noising algorithm which can remove different types of noises especially impulsive noises from digital images with high accuracy and at the same time preserving essential or vital image information such as edges, texture information etc. Here, in this paper, we propose an image de-noising algorithm based on an approximated fractional integrator (AFI), which overcomes the above-discussed issues efficiently. It has been employed for both black & white and grayscale images. For grayscale image (because of many intensity levels), we propose a new adaptive method for selection of fractional order (q) that depends on specific features such as gradient, entropy, local roughness, and contrast of the image. A hardware implementation of the proposed algorithm using NEXYS 4 DDR Artix-7, which is a low power FPGA device is done to further validate the performance of the proposed AFI based algorithm in a practical environment. Power consumption and resource utilization of the proposed algorithm is also addressed. Finally, three different quantitative parameters i.e., peak-signal-to-noise-ratio, structural similarity index and cross-correlation has been calculated, and the proposed method is compared with some state-of-the-art techniques, which validates the effectiveness of proposed algorithm especially if impulsive noise is present in digital images.













Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Anupriya, A., & Tayal, A. (2012). Wavelet based image denoising using self-organizing migration algorithm. CIIT International Journal of Digital Image Processing, 4(10), 542–546.
Aurich, V., & Weule, J. (1995). Non-linear Gaussian filters performing edge preserving diffusion. In G. Sagerer, S. Posch, & F. Kummert (Eds.), Mustererkennung 1995 (pp. 538–545). Berlin: Springer.
Bao, Q., Gao, J., & Chen, W. (2008). Local adaptive shrinkage threshold denoising using curvelet coefficients. Electronics Letters, 44(4), 277–278.
Black, M. J., Sapiro, G., Marimont, D. H., & Heeger, D. (1998). Robust anisotropic diffusion. IEEE Transactions on Image Processing, 7(3), 421–432.
Buades, A., Coll, B., & Morel, J. M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling & Simulation, 4(2), 490–530.
Cannistraci, C. V., Montevecchi, F. M., & Alessio, M. (2009). Median-modified wiener filter provides efficient denoising, preserving spot edge and morphology in 2-de image processing. Proteomics, 9(21), 4908–4919.
Chambolle, A. (2004). An algorithm for total variation minimization and applications. Journal of Mathematical imaging and vision, 20(1–2), 89–97.
Charoensak, C., & Sattar, F. (2007). FPGA design of a real-time implementation of dynamic range compression for improving television picture. In 2007 6th international conference on information, communications & signal processing (pp. 1–5). IEEE.
Chaudhury, K. N., Sage, D., & Unser, M. (2011). Fast \( o (1) \) bilateral filtering using trigonometric range kernels. IEEE Transactions on Image Processing, 20(12), 3376–3382.
Chen, F., Zhang, L., & Yu, H. (2015). External patch prior guided internal clustering for image denoising. In Proceedings of the IEEE international conference on computer vision (pp. 603–611).
Da Silva, R. D., Minetto, R., Schwartz, W. R., & Pedrini, H. (2013). Adaptive edge-preserving image denoising using wavelet transforms. Pattern Analysis and Applications, 16(4), 567–580.
Delkhosh, M. (2013). Introduction of derivatives and integrals of fractional order and its applications. Applied Mathematics and Physics, 1(4), 103–119.
Dong, W., Li, X., Zhang, L., & Shi, G. (2011). Sparsity-based image denoising via dictionary learning and structural clustering. In CVPR 2011 (pp. 457–464). IEEE.
Dutta, H., Hannig, F., Teich, J., Heigl, B., & Hornegger, H. (2006). A design methodology for hardware acceleration of adaptive filter algorithms in image processing. In IEEE 17th international conference on application-specific systems, architectures and processors (ASAP’06) (pp. 331–340). IEEE.
Gao, C., Zhou, J., Hu, J., & Lang, F. (2011). Edge detection of colour image based on quaternion fractional differential. IET Image Processing, 5(3), 261–272.
Getreuer, P. (2012). Rudin–Osher–Fatemi total variation denoising using split Bregman. Image Processing On Line, 2, 74–95.
Gonzalez, R. C., Woods, R. E., et al. (2002). Digital image processing
Hamza, A. B., Luque-Escamilla, P. L., Martínez-Aroza, J., & Román-Roldán, R. (1999). Removing noise and preserving details with relaxed median filters. Journal of Mathematical Imaging and Vision, 11(2), 161–177.
Hardie, R. C., & Barner, K. E. (1994). Rank conditioned rank selection filters for signal restoration. IEEE Transactions on Image Processing, 3(2), 192–206.
Jia, X., Liu, S., Feng, X., & Zhang, L. (2019). Focnet: A fractional optimal control network for image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 6054–6063).
Kokila, J., Ramasubramanian, N., & Naganathan, N. (2019). Resource efficient metering scheme for protecting SoC FPGA device and IPs in IOT applications. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 27(10), 2284–2295.
Kumar, B. S. (2013). Image denoising based on Gaussian/bilateral filter and its method noise thresholding. Signal, Image and Video Processing, 7(6), 1159–1172.
Kumar, S., Chauhan, S., Sundaram, G., Chouksey, M., & Jha, R. K. (2019a). An FPGA based practical implementation of stochastic resonance for image enhancement. In 25th international conference on noise and fluctuations (ICNF 2019), CONF.
Kumar, S., Gupta, A., & Jha, R. K. (2019b). Analysis, diagnosis and correction of rain streaks. In TENCON 2019-2019 IEEE region 10 conference (TENCON) (pp. 2700–2704). IEEE.
Kumar, S., & Jha, R. K. (2016). Enhancement of high dynamic range images using variational calculus regularizer with stochastic resonance. In Proceedings of the tenth Indian conference on computer vision, graphics and image processing (p. 38). ACM.
Kumar, S., & Jha, R. K. (2019). FD-based detector for medical image watermarking. IET Image Processing, 13(10), 1773–1782.
Kumar, S., Panna, B., & Jha, R. K. (2019c). Medical image encryption using fractional discrete cosine transform with chaotic function. Medical & Biological Engineering & Computing, 57(11), 2517–2533.
Lindoso, A., & Entrena, L. (2007). High performance FPGA-based image correlation. Journal of Real-Time Image Processing, 2(4), 223–233.
Luisier, F., Blu, T., & Unser, M. (2010). Image denoising in mixed Poisson–Gaussian noise. IEEE Transactions on Image Processing, 20(3), 696–708.
Manjon-Herrera, J. V. (2020). Non-local means filter. Retrieved July 20, 2019 from https://in.mathworks.com/matlabcentral/fileexchange/13176-non-local-means-filter.
Nakib, A., Schulze, Y., & Petit, E. (2012). Image thresholding framework based on two-dimensional digital fractional integration and legendre moments. IET Image Processing, 6(6), 717–727.
Perona, P., & Malik, J. (1990). Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(7), 629–639.
Pitas, I., & Venetsanopoulos, A. (1990). Nonlinear digital filters: Principles and applications. Hingham: Klumer Academic.
Pu, Y., Wang, W., Zhou, J., Wang, Y., & Jia, H. (2008). Fractional differential approach to detecting textural features of digital image and its fractional differential filter implementation. Science in China Series F: Information Sciences, 51(9), 1319–1339.
Rodriguez-Andina, J. J., Moure, M. J., & Valdes, M. D. (2007). Features, design tools, and application domains of FPGAs. IEEE Transactions on Industrial Electronics, 54(4), 1810–1823.
Rosado-Munoz, A., Bataller-Mompean, M., Soria-Olivas, E., Scarante, C., & Guerrero-Martinez, J. F. (2009). FPGA implementation of an adaptive filter robust to impulsive noise: Two approaches. IEEE Transactions on Industrial Electronics, 58(3), 860–870.
Saha, D., & Sur-Kolay, S. (2011). Secure public verification of IP marks in FPGA design through a zero-knowledge protocol. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 20(10), 1749–1757.
Samko, S. (2013). Fractional integration and differentiation of variable order: An overview. Nonlinear Dynamics, 71(4), 653–662.
Selesnick, I. W. (2004). The double-density dual-tree DWT. IEEE Transactions on Signal Processing, 52(5), 1304–1314.
Sethian, J. A. (1999). Level set methods and fast marching methods: evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science (Vol. 3). Cambridge: Cambridge University Press.
Sheng, H., Sun, H., Coopmans, C., Chen, Y., & Bohannan, G. (2011). A physical experimental study of variable-order fractional integrator and differentiator. The European Physical Journal Special Topics, 193(1), 93–104.
Tehranipoor, M., & Wang, C. (2011). Introduction to hardware security and trust. Berlin: Springer.
Trigeassou, J. C., Maamri, N., Sabatier, J., & Oustaloup, A. (2012). Transients of fractional-order integrator and derivatives. Signal, Image and Video Processing, 6(3), 359–372.
Vinh, T. Q., Park, J. H., Kim, Y. C., & Hong, S. H. (2008). FPGA implementation of real-time edge-preserving filter for video noise reduction. In 2008 international conference on computer and electrical engineering (pp. 611–614). IEEE.
Voloshynovskiy, S., Pereira, S., Pun, T., Eggers, J. J., & Su, J. K. (2001). Attacks on digital watermarks: Classification, estimation based attacks, and benchmarks. IEEE Communications Magazine, 39(8), 118–126.
Wang, Q., Yu, S., Li, C., Lü, J., Fang, X., Guyeux, C., et al. (2016). Theoretical design and FPGA-based implementation of higher-dimensional digital chaotic systems. IEEE Transactions on Circuits and Systems I: Regular Papers, 63(3), 401–412.
Wang, Z., Bovik, A. C., Sheikh, H. R., Simoncelli, E. P., et al. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4), 600–612.
Weickert, J. (1998). Anisotropic diffusion in image processing (Vol. 1). Stuttgart: Teubner Stuttgart.
Wen, B., Li, Y., & Bresler, Y. (2017). When sparsity meets low-rankness: Transform learning with non-local low-rank constraint for image restoration. In 2017 IEEE international conference on acoustics, speech and signal processing (ICASSP) (pp. 2297–2301). IEEE.
Xie, Q., Zhao, Q., Meng, D., Xu, Z., Gu, S., Zuo, W., & Zhang, L. (2016). Multispectral images denoising by intrinsic tensor sparsity regularization. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1692–1700).
Xie, Y., Gu, S., Liu, Y., Zuo, W., Zhang, W., & Zhang, L. (2016). Weighted schatten \( p \)-norm minimization for image denoising and background subtraction. IEEE Transactions on Image Processing, 25(10), 4842–4857.
Xu, J., Zhang, L., & Zhang, D. (2018). A trilateral weighted sparse coding scheme for real-world image denoising. In Proceedings of the European conference on computer vision (ECCV) (pp. 20–36).
Xu, J., Zhang, L., Zhang, D., & Feng, X. (2017). Multi-channel weighted nuclear norm minimization for real color image denoising. In Proceedings of the IEEE international conference on computer vision (pp. 1096–1104).
Xu, J., Zhang, L., Zuo, W., Zhang, D., & Feng, X. (2015). Patch group based nonlocal self-similarity prior learning for image denoising. In Proceedings of the IEEE international conference on computer vision (pp. 244–252).
Yang, R., Yin, L., Gabbouj, M., Astola, J., & Neuvo, Y. (1995). Optimal weighted median filtering under structural constraints. IEEE Transactions on Signal Processing, 43(3), 591–604.
Yue, Z., Yong, H., Zhao, Q., Meng, D., & Zhang, L. (2019). Variational denoising network: Toward blind noise modeling and removal. In Advances in neural information processing systems (pp. 1688–1699).
Zhang, J., & Liu, L. (2017). Publicly verifiable watermarking for intellectual property protection in FPGA design. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 25(4), 1520–1527.
Zhang, L., Dong, W., Zhang, D., & Shi, G. (2010). Two-stage image denoising by principal component analysis with local pixel grouping. Pattern Recognition, 43(4), 1531–1549.
Zhu, M., & Chan, T. (2008). An efficient primal-dual hybrid gradient algorithm for total variation image restoration. UCLA CAM Report, 34.
Acknowledgements
This publication is an outcome of the R&D work undertaken in the project under the Visvesvaraya PhD Scheme of Ministry of Electronics & Information Technology, Government of India, being implemented by Digital India Corporation (Formerly Media Lab Asia) (Grant No. U72900MH2001NPL133410).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Kumar, S., Jha, R.K. An FPGA-based design for a real-time image denoising using approximated fractional integrator. Multidim Syst Sign Process 31, 1317–1339 (2020). https://doi.org/10.1007/s11045-020-00709-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11045-020-00709-0