Skip to main content
Springer Nature Link
Log in

An hybrid denoising algorithm based on directional wavelet packets

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

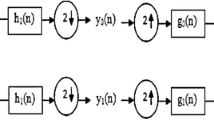
The paper presents an image denoising algorithm by combining a method that is based on directional quasi-analytic wavelet packets (qWPs) with the popular BM3D algorithm. The qWP-based denoising algorithm (qWPdn) consists of decomposition of the degraded image, application of adaptive localized soft thresholding to the transform coefficients using the Bivariate Shrinkage methodology, and restoration of the image from the thresholded coefficients from several decomposition levels. The combined method consists of several iterations of qWPdn and BM3D algorithms, where at each iteration the output from one algorithm updates the input to the other. The proposed methodology couples the qWPdn capabilities to capture edges and fine texture patterns even in the severely corrupted images with utilizing the sparsity in real images and self-similarity of patches in the image that is inherent in the BM3D. Multiple experiments, which compared the proposed methodology performance with the performance of six state-of-the-art denoising algorithms, confirmed that the combined algorithm was quite competitive.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

  1. The index n refers to the number of filters in the underlying one-dimensional complex tight framelet filter bank.

  2. \(s_{+}{\mathop {=}\limits ^{{\textit{def}}}}\max \{s, 0\}\).

  3. $$\begin{aligned}&{\textit{PSNR}}(\mathbf {x},{\tilde{\mathbf {x}}}){\mathop {=}\limits ^{{\textit{def}}}}10\log _{10}\left( \frac{K\,255^2}{\sum _{k=1}^K(x_{k}-\tilde{x}_{k})^2}\right) \; dB. \end{aligned}$$
    (3.2)

  4. For the “Seismic” image upqWP instead of upBM3D

  5. Averaged results from upBM3D are almost identical to those from hybrid algorithm.

References

  • Averbuch, A., Neittaanmäki, P., & Zheludev, V. (2020). Directional wavelet packets originating from polynomial splines. arXiv:2008.05364

  • Averbuch, A., Neittaanmäki, P., Zheludev, V., Salhov, M., & Hauser, J. (2021). Image inpainting using directional wavelet packets originating from polynomial splines. Signal Processing: Image Communication,, 97. arXiv:2001.04899

  • Averbuch, A., Coifman, R. R., Donoho, D. L., Israeli, M., & Shkolnisky, Y. (2008). A framework for discrete integral transformations I—The pseudopolar Fourier transform. SIAM Journal on Scientific Computing, 30(2), 764–784.

    Article  MathSciNet  MATH  Google Scholar 

  • Averbuch, A., Coifman, R. R., Donoho, D. L., Israeli, M., Shkolnisky, Y., & Sedelnikov, I. (2008). A framework for discrete integral transformations II—The 2d discrete Radon transform. SIAM Journal on Scientific Computing, 30(2), 785–803.

    Article  MathSciNet  MATH  Google Scholar 

  • Averbuch, A., Neittaanmäki, P., & Zheludev, V. (2019). Splines and spline wavelet methods with application to signal and image processing, Volume III: Selected topics. Springer.

  • Bayram, I., & Selesnick, I. W. (2008). On the dual-tree complex wavelet packet and m-band transforms. IEEE Transactions on Signal Processing, 56, 2298–2310.

    Article  MathSciNet  MATH  Google Scholar 

  • Binh, P. H. T., Cruz, C., & Egiazarian, K. (2021). Flashlight CNN image denoising. In 2020 28th European signal processing conference (EUSIPCO) (pp. 670–674).

  • Buades, A., Coll, B., & Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling & Simulation, 4(2), 490–530.

    Article  MathSciNet  MATH  Google Scholar 

  • Candés, E., Demanet, L., Donoho, D., & Ying, L. X. (2006). Fast discrete curvelet transforms. Multiscale Modeling & Simulation, 5, 861–899.

    Article  MathSciNet  MATH  Google Scholar 

  • Candés, E., & Donoho, D. (2004). New tight frames of curvelets and optimal representations of objects with piecewise \(c^{2}\) singularities. Communications on Pure and Applied Mathematics, 57, 219–266.

    Article  MathSciNet  MATH  Google Scholar 

  • Chen, Y., & Pock, T. (2017). Trainable nonlinear reaction diffusion: A flexible framework for fast and effective image restoration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 39(6), 1256–1272.

    Article  Google Scholar 

  • Che, Z., & Zhuang, X. (2018). Digital affine shear filter banks with 2-layer structure and their applications in image processing. IEEE Transactions on Image Processing, 27(8), 3931–3941.

    Article  MathSciNet  MATH  Google Scholar 

  • Coifman, R. R., & Wickerhauser, V. M. (1992). Entropy-based algorithms for best basis selection. IEEE Transactions on Information Theory, 38(2), 713–718.

    Article  MATH  Google Scholar 

  • Cruz, Cristóvão, Foi, Alessandro, Katkovnik, Vladimir, & Egiazarian, Karen. (2018). Nonlocality-reinforced convolutional neural networks for image denoising. IEEE Signal Processing Letters, 25(8), 1216–1220.

    Article  Google Scholar 

  • Dabov, K., Foi, A., Katkovnik, V., & Egiazarian, K. O. (2009). BM3D image denoising with shape adaptive principal component analysis. In Proceedings of the workshop on signal processing with adaptive sparse structured representations (SPARS’09).

  • Dabov, K., Foi, A., Katkovnik, V., & Egiazarian, K. (2007). Image denoising by sparse 3d transform-domain collaborative filtering. IEEE Transactions on Image Processing, 16(8), 2080–2095.

    Article  MathSciNet  Google Scholar 

  • Dong, W. S., Zhang, L., Shi, G. M., & Li, X. (2013). Nonlocally centralized sparse representation for image restoration. IEEE Transactions on Image Processing, 22(4), 1620–1630.

    Article  MathSciNet  MATH  Google Scholar 

  • Do, M. N., & Vetterli, M. (2008). Contourlets. In G. V. Welland (Ed.), Beyond wavelets. Academic Press.

  • Fang, Y., & Zeng, T. (2020). Learning deep edge prior for image denoising. Computer Vision and Image Understanding, 200, 103044.

    Article  Google Scholar 

  • Goyal, B., Dogra, A., Agrawal, S., Sohi, B. S., & Sharma, A. (2020). Image denoising review: From classical to state-of-the-art approaches. Information Fusion, 55, 220–244.

    Article  Google Scholar 

  • Gu, S., Zhang, L., Zuo, W., & Feng, X. (2014). Weighted nuclear norm minimization with application to image denoising. In 2014 IEEE conference on computer vision and pattern recognition (pp. 2862–2869).

  • Han, B., Mo, Q., Zhao, Z., & Zhuang, X. (2019). Directional compactly supported tensor product complex tight framelets with applications to image denoising and inpainting. SIAM Journal on Imaging Sciences, 12(4), 1739–1771.

    Article  MathSciNet  MATH  Google Scholar 

  • Han, B., & Zhao, Z. (2014). Tensor product complex tight framelets with increasing directionality. SIAM Journal on Imaging Sciences, 7(2), 997–1034.

    Article  MathSciNet  MATH  Google Scholar 

  • Han, B., Zhao, Z., & Zhuang, X. (2016). Directional tensor product complex tight framelets with low redundancy. Applied and Computational Harmonic Analysis, 41(2), 603–637.

    Article  MathSciNet  MATH  Google Scholar 

  • Hou, Y., & Shen, D. (2018). Image denoising with morphology- and size-adaptive block-matching transform domain filtering. EURASIP Journal on Image and Video Processing,59.

  • Ilesanmi, A. E., & Ilesanmi, T. O. (2021). Methods for image denoising using convolutional neural network: A review. Complex & Intelligent Systems, 7, 2179–2198.

    Article  Google Scholar 

  • Jalobeanu, A., Blanc-Féraud, L., & Zerubia, J. (2000). Satellite image deconvolution using complex wavelet packets. In Proc. IEEE Int. Conf. Image Process. (ICIP) (pp. 809–812).

  • Ji, H., Shen, Z., & Zhao, Y. (2017). Directional frames for image recovery: Multi-scale discrete Gabor frames. Journal of Fourier Analysis and Applications, 23(4), 729–757.

    Article  MathSciNet  MATH  Google Scholar 

  • Ji, H., Shen, Z., & Zhao, Y. (2018). Digital Gabor filters with MRA structure. SIAM Journal on Multiscale Modeling and Simulation, 16(1), 452–476.

    Article  MathSciNet  MATH  Google Scholar 

  • Kingsbury, N. G. (1999). Image processing with complex wavelets. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 357(1760), 2543–2560.

    Article  MATH  Google Scholar 

  • Kutyniok, G., & Labate, D. (2012). Shearlets: Multiscale analysis for multivariate data. Birkhäuser.

  • Lim, W.-Q., Kutyniok, G., & Zhuang, X. (2012). Digital shearlet transforms. In Shearlets: multiscale analysis for multivariate data (pp. 239–282). Birkhäuser.

  • Liu, J., & Osher, S. (2019). Block matching local SVD operator based sparsity and TV regularization for image denoising. Journal of Scientific Computing, 78, 607–624.

    Article  MathSciNet  MATH  Google Scholar 

  • Li, Xiaoxia, Xiao, Juan, Zhou, Yingyue, Ye, Yuanzheng, Lv, Nianzu, Wang, Xueyuan, et al. (2020). Detail retaining convolutional neural network for image denoising. Journal of Visual Communication and Image Representation, 71, 102774.

    Article  Google Scholar 

  • Mou, Chong, Zhang, Jian, Fan, Xiaopeng, Liu, Hangfan, & Wang, Ronggang. (2022). Cola-net: Collaborative attention network for image restoration. IEEE Transactions on Multimedia, 24, 1366–1377.

    Article  Google Scholar 

  • Quan, Yuhui, Chen, Yixin, Shao, Yizhen, Teng, Huan, Xu, Yong, & Ji, Hui. (2021). Image denoising using complex-valued deep CNN. Pattern Recognition, 111, 107639.

    Article  Google Scholar 

  • Romano, Y., & Elad, M. (2015). Boosting of image denoising algorithms. SIAM Journal on Imaging Sciences, 8(2), 1187–1219.

    Article  MathSciNet  MATH  Google Scholar 

  • Selesnick, I. W., Baraniuk, R. G., & Kingsbury, N. G. (2005). The dual-tree complex wavelet transform. IEEE Signal Processing Magazine, 22(6), 123–151.

    Article  Google Scholar 

  • Şendur, L., & Selesnick, I. W. (2002a). Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Transactions on Signal Processing, 50, 2744–2756.

  • Şendur, L., & Selesnick, I. (2002b). Bivariate shrinkage with local variance estimation. IEEE Signal Processing Letters, 9(12), 438–441.

  • Shi, Wuzhen, Jiang, Feng, Zhang, Shengping, Wang, Rui, Zhao, Debin, & Zhou, Huiyu. (2019). Hierarchical residual learning for image denoising. Signal Processing: Image Communication, 76, 243–251.

    Google Scholar 

  • Tian, C., Fei, L., Zheng, W., Zuo, W., Xu, Y., & Lin, C.-W. (2020). Deep learning on image denoising: An overview. Neural Networks,131.

  • Wang, Z., & Bovik, A. C. (2009). Mean squared error : Love it or leave it? IEEE Signal Processing Magazine, 26, 98–117.

    Article  Google Scholar 

  • Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4), 600–612.

    Article  Google Scholar 

  • Zhang, K., Zuo, W., Chen, Y., Meng, D., & Zhang, L. (2017). Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Transactions on Image Processing, 26(7), 3142–3155.

    Article  MathSciNet  MATH  Google Scholar 

  • Zhou, T., Li, C., Zeng, X., & Zhao, Y. (2021). Sparse representation with enhanced nonlocal self-similarity for image denoising. Machine Vision and Applications, 32(5), 1–11.

    Article  Google Scholar 

  • Zhuang, X. (2016). Digital affine shear transforms: Fast realization and applications in image/video processing. SIAM Journal on Imaging Sciences, 9(3), 1437–1466.

    Article  MathSciNet  MATH  Google Scholar 

  • Zhuang, X., & Han, B. (2019). Compactly supported tensor product complex tight framelets with directionality. In 2019 International conference on sampling theory and applications (SampTA), Bordeaux, France.

Download references

Acknowledgements

This research was partially supported by the Israel Science Foundation (ISF, 1556/17), Blavatnik Computer Science Research Fund Israel Ministry of Science and Technology 3-13601 and 3-14481.

Author information

Authors and Affiliations

  1. School of Computer Science, Tel Aviv University, Ramat Aviv, Tel Aviv, Israel

    Amir Averbuch, Valery Zheludev & Moshe Salhov

  2. Faculty of Mathematical Information Technology, University of Jyväskylä, Agora, Jyväskylä, Finland

    Pekka Neittaanmäki

  3. School of Electrical Engineering, Tel Aviv University, Ramat Aviv, Tel Aviv, Israel

    Jonathan Hauser

Authors
  1. Amir Averbuch
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Pekka Neittaanmäki
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Valery Zheludev
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Moshe Salhov
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Jonathan Hauser
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Amir Averbuch.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Matlab code for calculation of number of different orientations of real qWPs

Appendix: Matlab code for calculation of number of different orientations of real qWPs

figure f

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Averbuch, A., Neittaanmäki, P., Zheludev, V. et al. An hybrid denoising algorithm based on directional wavelet packets. Multidim Syst Sign Process 33, 1151–1183 (2022). https://doi.org/10.1007/s11045-022-00836-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11045-022-00836-w

Keywords