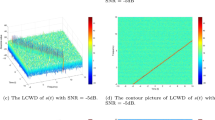
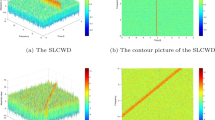
Abstract
This paper is to propose a new definition of two-dimensional (2D) Wigner distribution (2D-WD) and two-dimensional ambiguity function (2D-AF) associated with two-dimensional nonseparable linear canonical transform (2D-NS-LCT), namely 2D-NLCWD and 2D-NLCAF. This allows for several consequences of the basic properties of the proposed distributions such as the shift properties, the conjugation symmetry property, the marginal properties, the Moyal formula, and the relationships with the two-dimensional short-time Fourier transform (2D-STFT). Furthermore, we point out the usefulness and efficacy of newly defined distributions for detecting two-dimensional linear frequency-modulated (2D-LFM) signals.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data Availability
No datasets were generated or analysed during the current study.
References
Bai, R. F., Li, B. Z., & Cheng, Q. Y. (2012). Wigner-Ville distribution associated with the linear canonical transform. Journal of Applied Mathematics 1–14.
Che, T. W., Li, B. Z., & Xu, T. Z. (2012). The ambiguity function associated with the linear canonical transform. EURASIP Journal on Advances in Signal Processing, 138, 1–14.
Ding, J. J., & Pei, S. C. (2011). Eigenfunctions and self-imaging phenomena of the two-dimensional non-separable linear canonical transform. The Journal of the Optical Society of America, 28, 82–95.
Ding, J. J., Pei, S. C., & Liu, C. L. (2012). Improved implementation algorithms of the two-dimensional non-separable linear canonical transform. The Journal of the Optical Society of America, 29, 1615–1624.
Dong, P., & Galatsanos, N. P. (2002). Affine transformation resistant watermarking based on image normalization. IEEE International Conference on Image Processing, 3, 489–492.
Johnston, J. A. (1989). Wigner distribution and FM radar signal design. IEE Proceeding of F: Radar and Signal Process, 136, 81–88.
Koç, A., Ozaktas, H. M., & Hesselink, L. (2010). Fast and accurate computation of two-dimensional non-separable quadratic-phase integrals. The Journal of the Optical Society of America, 27, 1288–1302.
Liu, Z. J., Chen, H., Liu, T., Li, P. F., Dai, J. M., Sun, X. G., & Liu, S. T. (2010). Double-image encryption based on the affine transform and the gyrator transform. Journal of the Optic, 12, 035407.
Minh, L. T. (2023). Modified ambiguity function and Wigner distribution associated with quadratic-phase Fourier transform. The Journal of Fourier and Analysis and Application. Accepted (November 6, 2023).
Pei, S. C., & Ding, J. J. (2009). Properties, digital implementation, applications, and self image phenomena of the gyrator transform. In 17th European Signal Processing Conference (EUSIPCO) (Curran Associates, Inc.) (pp. 441–444).
Pei, S. C., & Ding, J. J. (2001). Two-dimensional affine generalized fractional Fourier transform. IEEE Transactions Signal Processing, 49(4), 878–897.
Pei, S. C., & Ding, J. J. (2010). Relations between fractional operations and time-frequency distributions and their applications. IEEE Transactions Signal Processing, 49, 1638–1655.
Pei, S. C., & Ding, J. J. (2010). Fractional Fourier transform: Wigner distribution, and filter design for stationary and nonstationary random processes. IEEE Transactions Signal Processing, 58, 4079–4092.
Ravi, K., Sheridan, J. T., & Basanta, B. (2018). Nonlinear double image encryption using 2D non-separable linear canonical transform and phase retrieval algorithm. Optics & Laser Technology, 107, 353–360.
Rodrigo, J. A., Alieva, T., & Calvo, M. L. (2007). Experimental implementation of the gyrator transform. The Journal of the Optical Society of America, 24, 3135–3139.
Rodrigo, J. A., Alieva, T., & Calvo, M. L. (2007). Applications of gyrator transform for image processing. Optics Communication, 278, 279–284.
Shah, F. A., & Teali, A. A. (2023). Scaling Wigner distribution in the framework of linear canonical transform. Circuits, Systems, and Signal Processing, 42, 1181–1205.
Teali, A. A., Shah, F. A., & Tantary, A. Y. (2023). Coupled fractional Wigner distribution with applications to LFM signals. Fractals, 31(02), 2340020.
Wei, D., & Shen, Y. (2022). New two-dimensional Wigner distribution and ambiguity function associated with the two-dimensional nonseparable linear canonical transform. Circuits, Systems, and Signal Processing, 41, 77–101.
Zayed, A. (2019). A new perspective on the two- dimensional fractional Fourier transform and its relationship with the Wigner distribution. The Journal of Fourier and Analysis and Application, 25(2), 460–487.
Zhang, Z. C. (2023). Uncertainty principle for free metaplectic transformation. The Journal of Fourier and Analysis and Application, 29(71).
Zhang, Z. C., & Lou, M. (2015). New integral transforms for generalizing the Wigner distribution and ambiguity function. IEEE Signal Processing Letters, 22(4).
Zhang, Z. C. (2016). Novel Wigner distribution and ambiguity function associated with the linear canonical transform domain. Optik, 127, 4995–5012.
Zhang, Z. C., Jiang, X., Qiang, S. Z., Sun, A., Liang, Z. Y., Shi, X., & Wu, A. Y. (2021). Y: Scaled Wigner distribution using fractional instantaneous autocorrelation. Optik, 237, 166691.
Zhang, Z. C., Zhu, Z., Li, D., & He, Y. (2023). Free metaplectic Wigner distribution: Definition and Heisenberg’s uncertainty principles. IEEE Transactions on Information Theory, 69(10), 6787–6810.
Zhao, L., Healy, J. J., & Sheridan, J. T. (2014). Two-dimensional nonseparable linear canonical transform: sampling theorem and unitary discretization. The Journal of the Optical Society of America, 31(12), 2631–2641.
Acknowledgements
The author would like to thank the anonymous referees very much for suggestions and valuable remarks which have helped to improve the exposition of the paper.
Author information
Authors and Affiliations
Contributions
L. T Minh wrote the main manuscript text and reviewed the manuscript.
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Minh, L.T. Novel two-dimensional Wigner distribution and ambiguity function in the framework of the two-dimensional nonseparable linear canonical transform. Multidim Syst Sign Process 35, 11–35 (2024). https://doi.org/10.1007/s11045-024-00886-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11045-024-00886-2
Keywords
- Wigner distribution
- Ambiguity function
- Nonseparable linear canonical transform
- Single-and multi-component LFM signal