Skip to main content
Springer Nature Link
Log in

On the complexity of nonuniform wavelength-based machine

  • Published:
Natural Computing Aims and scope Submit manuscript

Abstract

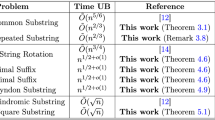
The wavelength-based machine, or simply w-machine, is an optical computational model, which is designed based on simultaneous movement of several wavelengths in a single light ray, and simultaneous effect of simple optical devices on them. In this paper, we investigate nonuniform complexity classes of w-machine, based on three complexity measures, namely, size, time, and word length. We show that the class of languages which can be generated by constant size nonuniform w-machines contain infinitely many Turing undecidable languages. Also, we show that polynomial size nonuniform w-machines generate all NP languages, and every NP-hard language requires at least polynomial time and polynomial size nonuniform w-machines to be generated. We prove that the class of languages which can be generated by polynomial size nonuniform w-machines is equal to NP/poly, and almost all languages require exponential size and polynomial time nonuniform w-machines to be generated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Barakat R, Reif JH (1987) Lower bounds on the computational efficiency of optical computing systems. Appl Opt 26(6):1015–1018

    Article  Google Scholar 

  • Beigel R, Kummer M, Stephan F (1995) Approximable sets. Inf Comput 120(2):304–314

    Article  MATH  MathSciNet  Google Scholar 

  • Chow TY (2011) Almost-natural proofs. J Comput Syst Sci 77(4):728–737

    Article  MATH  Google Scholar 

  • Demtrder W (2011) Atoms, molecules and photons: an introduction to atomic- molecular- and quantum physics, 2nd edn. Springer, Berlin

    Google Scholar 

  • Dolev S, Fitoussi H (2010) Masking traveling beams:optical solutions for np-complete problems, trading space for time. Theor Comput Sci 411:837–853

    Article  MATH  MathSciNet  Google Scholar 

  • Goliaei S (2012) Unconventional computing, an optical approach. Ph.D. Thesis, Tarbiat Modares University

  • Goliaei S, Foroughmand-Araabi MH (2012) Lower bounds on the complexity of the wavelength-based machine. In: Durand-Lose J, Jonoska N. (eds) Lecture notes in computer science, vol 7445. Springer, Berlin, Heidelberg 94–105

    Google Scholar 

  • Goliaei S, Jalili S (2009) An optical wavelength-based solution to the 3-SAT problem. In: Dolev S, Oltean M, (eds) Lecture Notes in Computer Science. Volume 5882. Springer-Verlag Berlin Heidelberg, pp 77–85

  • Goliaei S, Jalili S (2012) An optical solution to the 3-SAT problem using wavelength based selectors. J Supercomput 62:663–672

    Article  Google Scholar 

  • Goliaei S, Jalili S (2013) An optical wavelength-based computational machine. Int J Unconv Comput 9:97–123

    Google Scholar 

  • Goliaei S, Jalili S, Salimi J (2012) Light-based solution for the dominating set problem. Appl Opt 51(29):6979–6983

    Article  Google Scholar 

  • Haist T, Osten W (2007) An optical solution for the traveling salesman problem. Opt Express 15(16):10473–10482

    Article  Google Scholar 

  • Maier M (2008) Optical switching networks, 1st edn. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  • Meinders ER, Mijiritskii AV, van Pieterson L, Wuttig M (2006) Optical data storage: Phase-change media and recording, 1st edn. Springer, Berlin

    Google Scholar 

  • Muller DE (1956) Complexity in electronic switching circuits. IRE Trans Electron Comput 5(1):15–19

    Article  Google Scholar 

  • Muntean O, Oltean M (2009) Deciding whether a linear diophantine equation has solutions by using a light-based device. J Optoelectron Adv Mater 11(11):1728–1734

    Google Scholar 

  • Oltean M (2008) Solving the hamiltonian path problem with a light-based computer. Nat Comput 6(1):57–70

    Article  MathSciNet  Google Scholar 

  • Oltean M (2009) Light-based string matching. Nat Comput 8(1):121–132

    Article  MATH  MathSciNet  Google Scholar 

  • Oltean M, Muntean O (2008) Exact cover with light. New Gener Comput 26(4):329–346

    Article  MATH  Google Scholar 

  • Oltean M, Muntean O (2009) Solving the subset-sum problem with a light-based device. Nat Comput 8(2):321–331

    Article  MATH  MathSciNet  Google Scholar 

  • Reif JH, Tyagi A (1990) Energy complexity of optical computations. In: Proceedings of the 2nd IEEE symposium on parallel and distributed processing, pp 14–21

  • Reif JH, Tygar D, Yoshida A (1994) The computability and complexity of ray tracing. Discret Comput Geom 11:265–287

    Article  MATH  MathSciNet  Google Scholar 

  • Shannon C (1949) The synthesis of two-terminal switching circuits. Bell Syst Tech J 28(1):59–98

    Article  MathSciNet  Google Scholar 

  • Wegener I (2005) Complexity theory: exploring the limit of efficient algorithms, 1st edn. Springer, Berlin

    Google Scholar 

  • Woods D, Gibson J (2008) Lower bounds on the computational power of an optical model of computation. Nat Comput 7(1):95–108

    Article  MATH  MathSciNet  Google Scholar 

  • Woods D, Naughton TJ (2005) An optical model of computation. Theor Comput Sci 334(1–3):227–258

    Article  MATH  MathSciNet  Google Scholar 

  • Woods D, Naughton TJ (2008) Parallel and sequential optical computing. In: Dolev S, Haist T, Oltean M (eds) Lecture notes in computer science, vol 5172. Springer, Berlin, Heidelberg, pp 70–86

  • Woods D, Naughton TJ (2009) Optical computing. Appl Math Comput 215(4):1417–1430

    Article  MATH  MathSciNet  Google Scholar 

  • Yu FTS, Jutamulia S, Yin S (eds) (2001) Introduction to information optics, 1st edn. Academic Press, Boston

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Tehran, Tehran, Iran

    Sama Goliaei & Mohammad-Hadi Foroughmand-Araabi

Authors
  1. Sama Goliaei
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mohammad-Hadi Foroughmand-Araabi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Sama Goliaei.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Goliaei, S., Foroughmand-Araabi, MH. On the complexity of nonuniform wavelength-based machine. Nat Comput 13, 269–283 (2014). https://doi.org/10.1007/s11047-014-9412-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11047-014-9412-2

Keywords