Abstract
The field of structural DNA nanotechnology aims at the systematic development of self-assembling nanostructures using DNA as the construction material. Research in this area is progressing rapidly, and the controlled, computer-aided design of increasingly complex structures is becoming feasible. One thread of this endeavour is the design and characterisation of self-assembling 3D nanostructures based on wireframe polyhedral models. This article aims to illustrate some of the key developments in this direction, in sufficient detail so that the reader can achieve a general understanding of the main concepts and approaches. The emphasis is on the design principles rather than experimental methodology, and the role of computer science and computational tools is set forth.

Adapted with permission from Chen and Seeman (1991)

Reprinted with permission from Shih et al. (2004)

Reprinted with permission from Shih et al. (2004)

Reprinted with permission from He et al. (2008)

Reprinted with permission from He et al. (2008)

Adapted with permission from Rothemund (2006b)

Reprinted with permission from Rothemund (2006b)

Reprinted with permission from Douglas et al. (2009)

Reprinted with permission from Iinuma et al. (2014)

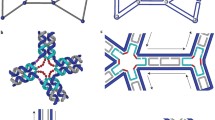
Reprinted with permission from Han et al. (2013)

Reprinted with permission from Han et al. (2013)

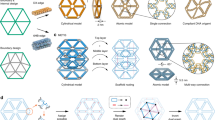
Adapted with permission from Benson et al. (2015)

Adapted with permission from Benson et al. (2015)

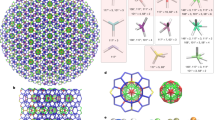
Adapted with permission from Veneziano et al. (2016)

Reprinted with permission from Veneziano et al. (2016)
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
We use the standard abbreviations ssDNA = single-stranded DNA, dsDNA = double-stranded DNA.
nt = nucleotide.
An interesting non-origami approach to volume-filling 3D designs, using DNA “bricks”, is presented in (Ke et al. 2012).
In fact, a cube is not an ideal test structure for DNA polyhedral designs, because unless the corner joints are stiff, a wireframe cube is not structurally rigid, i.e. in a rod-hinge model it flexes. A tetrahedron or any other convex polyhedron with only triangular faces would not have this problem (Cromwell 1999, Chapter 6).
It is noted in passing at the end of (Shih et al. 2004) that their design could be simplified further, with some loss of rigidity, by replacing the DX struts by simple duplex struts, and the PX struts by hairpin loops that are first cleaved open by restriction enzymes and then joined by ligation to their partners. One of the reviewers of the present survey also asked if the design could be based on DX-type struts alone. From the strand routing point of view this would seem to be possible, however with the backbone strand crossing itself at some point(s), so that one would need to take care also that the planned routing does not form a knot (cf. Sect. 4.2). The folding of this type of design has most likely not been experimentally tested.
A polyhedron is simplicial if it is homeomorphic (i.e. inflatable to) a sphere. It is trivalent if all vertices have exactly three neighbours.
This specific connection is recognised and summarised in (Rothemund 2006b) with elegant conciseness: “William Shih has observed that single-stranded origami may be used to create arbitrary polygonal networks. To see this, replace helper joins with paranemic cohesion motifs and scaffold joins with Shih’s double-crossover struts in all the diagrams of this section”.
The name A-trail presumably derives from the sharp “A-like” turns the path makes at each vertex.
More precisely, the problem is known to be NP-complete in Eulerian polyhedral graphs (Døvling Andersen and Fleischner 1995), but not in triangulated Eulerian polyhedral graphs. In fact, Fleischner (1990) conjectured that every triangulated Eulerian polyhedral graph has an A-trail, but even under this assumption, no polynomial time algorithm is known for finding such.
References
Benson E, Mohammed A, Gardell J et al (2015) DNA rendering of polyhedral meshes at the nanoscale. Nature 523:441–444. doi:10.1038/nature14586
Brenneman A, Condon A (2002) Strand design for biomolecular computation. Nat Comput 287:39–58. doi:10.1016/S0304-3975(02)00135-4
Chandrasekaran AR, Anderson N, Kizer M et al (2016a) Beyond the fold: emerging biological applications of DNA origami. ChemBioChem 17:1081–1089. doi:10.1002/cbic.201600038
Chandrasekaran AR, Pushpanathan M, Halvorsen K (2016b) Evolution of DNA origami scaffolds. Mater Lett 170:221–224. doi:10.1016/j.matlet.2016.01.161
Chen J, Seeman NC (1991) Synthesis from DNA of a molecule with the connectivity of a cube. Nature 350:631–633. doi:10.1038/350631a0
Cooper JP, Hagerman PJ (1987) Gel electrophoretic analysis of the geometry of a DNA four-way junction. J Mol Biol 198:711–719. doi:10.1016/0022-2836(87)90212-9
Cormen TH, Leiserson CE, Rivest RL, Stein C (2009) Introduction to algorithms, 3rd edn. MIT Press, Cambridge
Cromwell PR (1999) Polyhedra. Cambridge University Press, Cambridge
Diestel R (2017) Graph theory, 5th edn. Springer, Berlin
Dietz H, Douglas SM, Shih WM (2009) Folding DNA into twisted and curved nanoscale shapes. Science 325:725. doi:10.1126/science.1174251
Dirks RM, Lin M, Winfree E, Pierce NA (2004) Paradigms for computational nucleic acid design. Nucleic Acids Res 32:1392–1403. doi:10.1093/nar/gkh291
Douglas SM, Dietz H, Liedl T et al (2009) Self-assembly of DNA into nanoscale three-dimensional shapes. Nature 459:414–418. doi:10.1038/nature08016
Døvling Andersen L, Fleischner H (1995) The NP-completeness of finding A-trails in Eulerian graphs and of finding spanning trees in hypergraphs. Discrete Appl Math 59:203–214. doi:10.1016/0166-218X(95)80001-K
Edmonds J (1965) Paths, trees, and flowers. Can J Math 17:449–467. doi:10.4153/CJM-1965-045-4
Ellis-Monaghan JA, McDowell A, Moffatt I, Pangborn G (2015) DNA origami and the complexity of Eulerian circuits with turning costs. Nat Comput 14:491–503. doi:10.1007/s11047-014-9457-2
Ellis-Monaghan JA, Pangborn G, Seeman NC et al (2017) Design tools for reporter strands and DNA origami scaffold strands. Theor Comput Sci 671:69–78. doi:10.1016/j.tcs.2016.10.007
Euler L (1741) Solutio problematis ad geometriam situs pertinentis. Comment Acad Sci Petropolitanae 8:128–140
Feldkamp U, Niemeyer CM (2006) Rational design of DNA nanoarchitectures. Angew Chem Int Ed 45:1856–1876. doi:10.1002/anie.200502358
Fleischner H (1990) Eulerian graphs and related topics. Elsevier North Holland, Amsterdam
Fu TJ, Seeman NC (1993) DNA double-crossover molecules. Biochemistry (Mosc) 32:3211–3220. doi:10.1021/bi00064a003
Gibson DG, Young L, Chuang R-Y et al (2009) Enzymatic assembly of DNA molecules up to several hundred kilobases. Nat Methods 6:343–345. doi:10.1038/nmeth.1318
Gibson DG, Smith HO, Hutchison CA et al (2010) Chemical synthesis of the mouse mitochondrial genome. Nat Methods 7:901–903. doi:10.1038/nmeth.1515
Goodman RP, Berry RM, Turberfield AJ (2004) The single-step synthesis of a DNA tetrahedron. Chem Commun 40:1372–1373. doi:10.1039/B402293A
Goodman RP, Schaap IAT, Tardin CF et al (2005) Rapid chiral assembly of rigid DNA building blocks for molecular nanofabrication. Science 310:1661. doi:10.1126/science.1120367
Gür FN, Schwarz FW, Ye J et al (2016) Toward self-assembled plasmonic devices: high-yield arrangement of gold nanoparticles on DNA origami templates. ACS Nano 10:5374–5382. doi:10.1021/acsnano.6b01537
Han D, Pal S, Nangreave J et al (2011) DNA origami with complex curvatures in three-dimensional space. Science 332:342. doi:10.1126/science.1202998
Han D, Pal S, Yang Y et al (2013) DNA gridiron nanostructures based on four-arm junctions. Science 339:1412. doi:10.1126/science.1232252
He Y, Chen Y, Liu H et al (2005) Self-assembly of hexagonal DNA two-dimensional (2D) arrays. J Am Chem Soc 127:12202–12203. doi:10.1021/ja0541938
He Y, Ye T, Su M et al (2008) Hierarchical self-assembly of DNA into symmetric supramolecular polyhedra. Nature 452:198–201. doi:10.1038/nature06597
Hughes RA, Ellington AD (2017) Synthetic DNA synthesis and assembly: putting the synthetic in synthetic biology. Cold Spring Harb Perspect Biol. doi:10.1101/cshperspect.a023812
Iinuma R, Ke Y, Jungmann R et al (2014) Polyhedra self-assembled from DNA tripods and characterized with 3D DNA-PAINT. Science 344:65. doi:10.1126/science.1250944
Kallenbach NR, Ma R-I, Seeman NC (1983) An immobile nucleic acid junction constructed from oligonucleotides. Nature 305:829–831. doi:10.1038/305829a0
Ke Y, Sharma J, Liu M et al (2009) Scaffolded DNA origami of a DNA tetrahedron molecular container. Nano Lett 9:2445–2447. doi:10.1021/nl901165f
Ke Y, Ong LL, Shih WM, Yin P (2012) Three-dimensional structures self-assembled from DNA bricks. Science 338:1177. doi:10.1126/science.1227268
Klavžar S, Rus J (2013) Stable traces as a model for self-assembly of polypeptide nanoscale polyhedrons. MATCH Commun Math Comput Chem 70:317–330. http://match.pmf.kg.ac.rs/content70n1.htm
Krishnan Y, Simmel FC (2011) Nucleic acid based molecular devices. Angew Chem Int Ed 50:3124–3156. doi:10.1002/anie.200907223
Kuzyk A, Schreiber R, Fan Z et al (2012) DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 483:311–314. doi:10.1038/nature10889
Li X, Yang X, Qi J, Seeman NC (1996) Antiparallel DNA double crossover molecules as components for nanoconstruction. J Am Chem Soc 118:6131–6140. doi:10.1021/ja960162o
Linko V, Nummelin S, Aarnos L et al (2016) DNA-based enzyme reactors and systems. Nanomaterials 6:139. doi:10.3390/nano6080139
Marchi AN, Saaem I, Vogen BN et al (2014) Toward larger DNA origami. Nano Lett 14:5740–5747. doi:10.1021/nl502626s
Mohammed A, Hajij M (2017) Unknotted strand routings of triangulated meshes. In: Proceedings, 23rd international conference on DNA computing and molecular programming, pp 46–63. doi:10.1007/978-3-319-66799-7_4
Morse A, Adkisson W, Greene J et al (2017) DNA origami and unknotted A-trails in torus graphs. arXiv.org. https://arxiv.org/abs/1703.03799
Pinheiro AV, Han D, Shih WM, Yan H (2011) Challenges and opportunities for structural DNA nanotechnology. Nat Nano 6:763–772. doi:10.1038/nnano.2011.187
Rothemund PWK (2006a) Folding DNA to create nanoscale shapes and patterns. Nature 440:297–302. doi:10.1038/nature04586
Rothemund PWK (2006b) Scaffolded DNA origami: from generalized multicrossovers to polygonal networks. In: Chen J, Jonoska N, Rozenberg G (eds) Nanotechnology: science and computation. Springer, Berlin, pp 3–21. doi:10.1007/3-540-30296-4_1
Seeman NC (1981) Nucleic acid junctions: building blocks for genetic engineering in three dimensions. In: Sarma RH (ed) Biomolecular stereodynamics. Adenine Press, New York, pp 269–277
Seeman NC (1982) Nucleic acid junctions and lattices. J Theor Biol 99:237–247. doi:10.1016/0022-5193(82)90002-9
Seeman NC (2001) DNA nicks and nodes and nanotechnology. Nano Lett 1:22–26. doi:10.1021/nl000182v
Seeman NC (2010) Nanomaterials based on DNA. Annu Rev Biochem 79:65–87. doi:10.1146/annurev-biochem-060308-102244
Seeman NC (2015) Structural DNA nanotechnology. Cambridge University Press, Cambridge
Seeman NC, Kallenbach NR (1983) Design of immobile nucleic acid junctions. Biophys J 44:201–209. doi:10.1016/S0006-3495(83)84292-1
Shih WM, Quispe JD, Joyce GF (2004) A 1.7-kilobase single-stranded DNA that folds into a nanoscale octahedron. Nature 427:618–621. doi:10.1038/nature02307
Tian Y, Wang T, Liu W et al (2015) Prescribed nanoparticle cluster architectures and low-dimensional arrays built using octahedral DNA origami frames. Nat Nano 10:637–644. doi:10.1038/nnano.2015.105
Veneziano R, Ratanalert S, Zhang K et al (2016) Designer nanoscale DNA assemblies programmed from the top down. Science. doi:10.1126/science.aaf4388
Zhang Y, Seeman NC (1994) Construction of a DNA-truncated octahedron. J Am Chem Soc 116:1661–1669. doi:10.1021/ja00084a006
Zhang C, Su M, He Y et al (2008) Conformational flexibility facilitates self-assembly of complex DNA nanostructures. Proc Natl Acad Sci 105:10665–10669. doi:10.1073/pnas.0803841105
Zhang F, Nangreave J, Liu Y, Yan H (2014) Structural DNA nanotechnology: state of the art and future perspective. J Am Chem Soc 136:11198–11211. doi:10.1021/ja505101a
Zhang F, Jiang S, Wu S et al (2015) Complex wireframe DNA origami nanostructures with multi-arm junction vertices. Nat Nano 10:779–784. doi:10.1038/nnano.2015.162
Zhao Z, Fu J, Dhakal S et al (2016) Nanocaged enzymes with enhanced catalytic activity and increased stability against protease digestion. Nat Commun 7:10619. doi:10.1038/ncomms10619
Acknowledgements
Preparing this survey was made possible by a sabbatical leave from Aalto University, and most of it was written during stays at ETH Zürich (host Prof. Roger Wattenhofer), the University of Electro-Communications in Tokyo (host Prof. Shinnosuke Seki) and the Tokyo Institute of Technology (host Prof. Osamu Watanabe). I am very grateful for this opportunity. I also thank the two anonymous reviewers for their constructive and insightful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Orponen, P. Design methods for 3D wireframe DNA nanostructures. Nat Comput 17, 147–160 (2018). https://doi.org/10.1007/s11047-017-9647-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11047-017-9647-9