Skip to main content
Springer Nature Link
Log in

Stability and Bifurcation of a Class of Discrete-Time Cohen–Grossberg Neural Networks with Discrete Delays

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

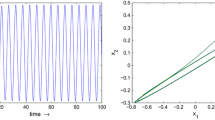
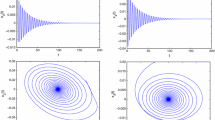
A class of discrete-time Cohen–Grossberg neural networks with discrete delays and ring-architecture are investigated in this paper. By analyzing the corresponding characteristic equations, the existence of Neimark–Sacker bifurcations at the origin are obtained. By applying the normal form theory and the center manifold theorem, the direction of the Neimark–Sacker bifurcation and the stability of bifurcating periodic solutions are obtained. Sufficient conditions to guarantee the global stability of the null solution of such networks are established by using suitable Lyapunov function and the properties of M-matrix. Numerical simulations are given to illustrate the obtained results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Cohen M, Grossberg S (1983) Absolute stability and global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans Syst Man Cybern 13:815–826

    Article  MATH  MathSciNet  Google Scholar 

  2. Hopfield JJ (1982) Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci USA 79:2554–2558

    Article  MathSciNet  Google Scholar 

  3. Zhao H, Chen Q, Xu S (2009) H-infinity guaranteed cost control for uncertain Markovian jump systems with mode-dependent distributed and input delays. J Franklin Inst 346:945–957

    Article  MATH  MathSciNet  Google Scholar 

  4. Shen H, Xu S, Lu J, Zhou J (2012) Passivity-based control for uncertain stochastic jumping systems with mode-dependent round-trip time delays. J Franklin Inst 349:1665–1680

    Article  MATH  MathSciNet  Google Scholar 

  5. Rakkiyappan R, Balasubramaniam P (2008) New global exponential stability results for neutral type neural networks with distributed time delays. Neurocomputing 71:1039–1045

    Article  Google Scholar 

  6. Wu Z, Shi P, Su H, Chu J Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled-data. IEEE Trans Cybern. doi:10.1109/TSMCB.2012.2230441

  7. Chen Y, Zheng W Stability analysis of time-varying neural networks subject to stochastic perturbations. IEEE Trans Cybern. doi:10.1109/TCYB.2013.2240451

  8. Cao J, Liang J (2004) Boundedness and stability for Cohen–Grossberg neural networks with time-varying delays. J Math Anal Appl 296:665–685

    Article  MATH  MathSciNet  Google Scholar 

  9. Ren F, Cao J (2007) Periodic solutions for a class of higher-order Cohen–Grossberg type neural networks with delays. Comput Math Appl 54:826–839

    Article  MATH  MathSciNet  Google Scholar 

  10. Song Q, Zhang J (2008) Global exponential stability of impulsive Cohen–Grossberg neural networks with time-varying delays. Nonlinear Anal RWA 9:500–510

    Article  MATH  MathSciNet  Google Scholar 

  11. Yang X (2009) Existence and global exponential stability of periodic solution for Cohen–Grossberg shunting inhibitory cellular neural networks with delays and impulses. Neurocomputing 72:2219–2226

    Article  Google Scholar 

  12. Huang Z, Feng C, Mohamad S (2012) Multistability analysis for a general class of delayed Cohen–Grossberg neural networks. Inf Sci 187:233–244

    Article  MATH  MathSciNet  Google Scholar 

  13. Zhang Z, Zhang T, Huang S, Xiao P (2012) New global exponential stability result to a general Cohen–Grossberg neural networks with multiple delays. Nonlinear Dyn 67:2419–2432

    Article  MATH  MathSciNet  Google Scholar 

  14. Townley S, Ilchmann S, Weiss A et al (2000) Existence and learning of oscillations in recurrent neural networks. IEEE Trans Neural Netw 11:205–214

    Article  Google Scholar 

  15. Huang Z, Xia Y (2009) Exponential periodic attractor of impulsive BAM networks with nite distributed delays. Chaos Solitons Fract 39:373–384

    Article  MATH  MathSciNet  Google Scholar 

  16. Wei J, Ruan S (1999) Stability and bifurcation in a neural network model with two delays. Phys D 130:255–272

    Article  MATH  MathSciNet  Google Scholar 

  17. Zhao H, Wang L (2007) Hopf bifurction in Cohen–Grossberg neural network with distributed delays. Nonlinear Anal RWA 8:73–89

    Article  MATH  Google Scholar 

  18. Guo S, Tang X, Huang L (2008) Stability and bifurcation in a discrete system of two neurons with delays. Nonlinear Anal RWA 9:1323–1335

    Article  MATH  MathSciNet  Google Scholar 

  19. Kaslik E, Balint S (2009) Complex and chaotic dynamics in a discrete-time-delayed Hopfield neural network with ring architecture. Neural Netw 22:1411–1418

    Article  Google Scholar 

  20. Xu G (2012) Neimark–Sacker bifurcation analysis for a discrete-time system of two neurons. Abstract Appl Anal. Article ID: 546356

  21. Wang J, Zhang C (2012) Symmetry discrete-time delayed neural network. Adv Differ Equ 2012:207

  22. Xiong W, Cao J (2005) Global exponential stability of discrete-time Cohen–Grossberg neural networks. Neurocomputing 64:433–446

    Article  Google Scholar 

  23. Li W, Pang L, Sua H, Wang K (2012) Global stability for discrete Cohen–Grossberg neural networks with finite and infinite delays. Appl Math Lett 25:2246–2251

    Article  MATH  MathSciNet  Google Scholar 

  24. Zhao H, Wang L (2006) Stability and bifurcation for discrete-time Cohen–Grossberg neural networks. Appl Math Comput 179:787–798

    Article  MATH  MathSciNet  Google Scholar 

  25. Liu Q, Xu R, Wang Z (2011) Stability and bifurcation of a class of discrete-time Cohen–Grossberg neural networks with delays. Discret Dyn Nat Soc. Article ID 403873

  26. Kuznetsov A (1998) Elements of applied bifurcation theory. Springer, New York

    MATH  Google Scholar 

  27. Kuznetsov A, Meijer H (2005) Numerical normal forms for codim 2 bifurcations of fixed points with at most two critical eigenvalues. SIAM J Sci Comput 26:1932–1954

    Article  MATH  MathSciNet  Google Scholar 

  28. Varga RS (2000) Matrix iterative analysis. Springer, Berlin

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Applied Mathematics, Shijiazhuang Mechanical Engineering College, Shijiazhuang, 050003, China

    Qiming Liu

  2. Department of Information Engineering, Shijiazhuang Mechanical Engineering College, Shijiazhuang, 050003, China

    Sumin Yang

Authors
  1. Qiming Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Sumin Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qiming Liu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, Q., Yang, S. Stability and Bifurcation of a Class of Discrete-Time Cohen–Grossberg Neural Networks with Discrete Delays. Neural Process Lett 40, 289–300 (2014). https://doi.org/10.1007/s11063-013-9329-2

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-013-9329-2

Keywords