Abstract
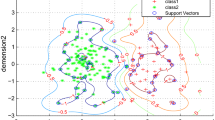
We consider the imbalanced learning problem, where the data associated with one class are far fewer than those associated with the other class. Current imbalanced learning methods often handle this problem by adapting certain intermediate parameters so as to impose a bias on the minority data. However, most of these methods are in rigorous and need to adapt those factors via the trial-and-error procedure. Recently, a new model called Biased Minimax Probability Machine (BMPM) presents a rigorous and systematic work and has demonstrated very promising performance on imbalance learning. Despite its success, BMPM exclusively relies on global information, namely, the first order and second order data information; such information might be however unreliable, especially for the minority data. In this paper, we propose a new model called One-Side Probability Machine (OSPM). Different from the previous approaches, OSPM can lead to rigorous treatment on biased classification tasks. Importantly, the proposed OSPM exploits the reliable global information from one side only, i.e., the majority class, while engaging the robust local learning from the other side, i.e., the minority class. To our best knowledge, OSPM presents the first model capable of learning data both locally and globally. Our proposed model has also established close connections with various famous models such as BMPM, Support Vector Machine, and Maxi-Min Margin Machine. One appealing feature is that the optimization problem involved in the novel OSPM model can be cast as a convex second order conic programming problem with the global optimum guaranteed. A series of experimental results on three data sets demonstrate the advantages of our proposed methods over four competitive approaches.


Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
Readers could refer to [9] on why SVM is regarded as one typical local learning model.
Note that it is straightforward to extend binary classification to multi-class problems via the strategy of one versus one or one versus others.
Despite the linear version discussion in the previous sections, it is straightforward to extend OSPM to the non-linear case via standard kernelization.
References
Boyd S, Vandenberghe L (2004) Convex optimization. Cambridge University Press, Cambridge, MA
Cardie C, Howe N (1997) Improving minority class prediction using case specific feature weights. In: Proceedings of the fourteen international conference on machine learning (ICML-1997). Morgan Kaufmann, San Francisco, CA, pp 57–65
Chawla N, Bowyer K, Hall L, Kegelmeyer W (2002) Smote: sythetic minority over-sampling technique. J Artif Intell Res 16:321–357
He H, Garcia E (2009) Learning from imbalanced data. IEEE Trans Knowl Data Eng 21(9):1263–1284
Huang K, Yang H, King I, Lyu MR (2004) Learning classifiers from imbalanced data based on biased minimax probability machine. In: Proceedings of CVPR, vol 2, pp 558–563
Huang K, Yang H, King I, Lyu MR (eds) (2004) Learning large margin classifiers locally and globally. In: Russ Greiner and Dale Schuurmansitors proceedings of the twenty-first international conference on machine learning (ICML-2004), pp 401–408
Huang K, Yang H, King I, Lyu MR (2006) Maximizing sensitivity in medical diagnosis using biased minimax probability machine. IEEE Trans Biomed Eng 53:821–831
Huang K, Yang H, King I, Lyu MR (2008) Machine learning: modeling data locally and gloablly. Springer, Berlin, ISBN 3-5407-9451-4
Huang K, Yang H, King I, Lyu MR (2008) Maxi-min margin machine: learning large margin classifiers globally and locally. IEEE Trans Neural Netw 19:260–272
Huang K, Yang H, King I, Lyu MR (2006) Imbalanced learning with biased minimax probability machine. IEEE Trans Syst Man Cybern Part B 36(4):913–923
Huang K, Yang H, King I, Lyu MR, Chan L (2004) The minimum error minimax probability machine. J Mach Learn Res 5:1253–1286
Huang K, Zheng D, Sun J, Hotta Y, Fujimoto K, Naoi S (2010) Sparse learning for support vector classification. Pattern Recognit Lett 31(13):1944–1951
Krawczyk B, Wozniak M, Schaefer G (2014) Cost-sensitive decision tree ensembles for effective imbalanced classification. Appl Soft Comput 14:554–562
Kubat M, Matwin S (1997) Addressing the curse of imbalanced training sets: one-sided selection. In: Proceedings of the fourteen international conference on machine learning (ICML-1997). Morgan Kaufmann, San Francisco, CA, pp 179–186
Lanckriet GRG, Ghaoui LE, Bhattacharyya C, Jordan MI (2002) A robust minimax approach to classification. J Mach Learn Res 3:555–582
Ling C, Li C (1998) Data mining for direct marketing:problems and solutions. In: Proceedings of the fourth international conference on knowledge discovery and data mining (KDD-1998). AAAI Press, Menlo Park, CA, pp 73–79
Lobo M, Vandenberghe L, Boyd S, Lebret H (1998) Applications of second order cone programming. Linear Algebra Appl 284:193–228
Maloof MA, Langley P, Binford TO, Nevatia R, Sage S (2003) Improved rooftop detection in aerial images with machine learning. Mach Learn 53:157–191
Provost F (2000) Learning from imbanlanced data sets. In: Proceedings of the seventeenth national conference on artificial intelligence (AAAI-2000)
Schmidt P, Witte A (1988) Predicting recidivism using survival models. Springer, New York
Vapnik VN (2000) The nature of statistical learning theory, 2nd edn. Springer, New York
Zhang R, Huang K (2013) One-side probability machine: Learning imbalanced classifiers locally and globally. In: Proceedings of international conference on neural information processing (ICONIP-2013), pp 140–147
Acknowledgments
The research was partly supported by the National Basic Research Program of China (2012CB316301) and the National Natural Science Foundation of China (61075052 and 61105018).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Huang, K., Zhang, R. & Yin, XC. Learning Imbalanced Classifiers Locally and Globally with One-Side Probability Machine. Neural Process Lett 41, 311–323 (2015). https://doi.org/10.1007/s11063-014-9370-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-014-9370-9