Abstract
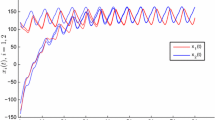
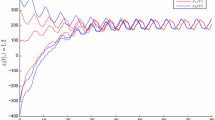
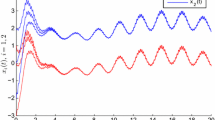
This paper concerns with the pseudo almost periodic solutions for a class of cellular neural networks model with multi-proportional delays. By applying contraction mapping fixed point theorem and differential inequality techniques, we establish some sufficient conditions for the existence and exponential stability of pseudo almost periodic solutions for the model, which improve and supplement existing ones. Moreover, an example and its numerical simulation are given to support the theoretical results.

Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Fink AM (1974) Almost periodic differential equations, vol 377. Lecture Notes in mathematics. Springer, Berlin
Zhang C (2003) Almost periodic type functions and ergodicity. Kluwer Academic/Science Press, Beijing
NGu érékata GM (2001) Almost automorphic functions and almost periodic functions in abstract spaces. Kluwer Academic, Plenum Publishers, New York
Liu B, Huang L (2005) Existence and exponential stability of almost periodic solutions for cellular neural networks with time-varying delays. Phys Lett A 341(1–4):135–144
Liu B, Huang L (2008) Positive almost periodic solutions for recurrent neural networks. Nonlinear Anal Real World Appl 9:830–841
Lu W, Chen T (2005) Global exponential stability of almost periodic solutions for a large class of delayed dynamical systems. Sci China Ser A Math 8(48):1015–1026
Xu Y (2014) New results on almost periodic solutions for CNNs with time-varying leakage delays. Neural Comput Appl 25:1293–1302
Zhang H, Shao J (2013) Existence and exponential stability of almost periodic solutions for CNNs with time-varying leakage delays. Neurocomputing 121(9):226–233
Zhang H, Shao J (2013) Almost periodic solutions for cellular neural networks with time-varying delays in leakage terms. Appl Math Comput 219(24):11471–11482
Zhang H (2014) Existence and stability of almost periodic solutions for CNNs with continuously distributed leakage delays. Neural Comput Appl 2014(24):1135–1146
Liu B, Tunc C (2015) Pseudo almost periodic solutions for CNNs with leakage delays and complex deviating arguments. Neural Comput Appl 26:429–435
Liu B (2015) Pseudo almost periodic solutions for neutral type CNNs with continuously distributed leakage delays. Neurocomputing 148:445–454
Liu B (2015) Pseudo almost periodic solutions for CNNs with continuously distributed leakage delays. Neural Process Lett 42:233–256
Dovrolis C, Stiliadisd D, Ramanathan P (1999) Proportional differentiated services: delay differentiation and packet scheduling. ACM Sigcomm Comput Commun Rev 29(4):109–120
Zhang Y, Zhou L (2012) Exponential stability of a class of cellular neural networks with multi-pantograph delays. Acta Electron Sin 40(6):1159–1163
Zhou L (2013) Delay-dependent exponential stability of cellular neural networks with multi-proportional delays. Neural Process Lett 38:347–359
Zhou L, Liu J (2013) Global asymptotic stability of a class of cellular neural networks with proportional delays. Chin J Eng Math 5(30):673–682
Zhou L, Zhang Y (2015) Global exponential stability of cellular neural networks with multi-proportional delays. Int J Biomath 8(6):1–17
Zhou L (2015) Novel global exponential stability criteria for hybrid BAM neural networks with proportional delays. Neurocomputing 161:99–106
Li J, Wei H, Liu T, Patrick Zhao X (2013) GPLEXUS: enable genome-scale gene association network reconstruction and analysis for very large-scale expression data. Nucleic Acids Res 42(5):1635–1645
Fox L, Mayers DF, Ockendon JR, Tayler AB (1971) On a functional-differential equation. J Inst Math Appl 8(3):271–307
Wu J (2001) Introduction to neural dynamics and signal trasmission delay. Walter de Gruyter, Berlin
Song X, Zhao P, Xing Z, Peng J (2016) Global asymptotic stability of CNNs with impulses and multi-proportional delays. Sci Math Methods Appl 39:722–733
Derfel GA (1990) Kato problem for functional-differential equations and difference Schrödinger operators. Oper Theory 46:319–321
Hale JK, Verduyn Lunel SM (1993) Introduction to functional differential equations. Springer-Verlag, New York
Zhang C (1995) Pseudo almost periodic solutions of some differential equations II. J Math Anal Appl 192:543–561
Acknowledgments
The author would like to express the sincere appreciation to the reviewers for their helpful comments in improving the presentation and quality of the paper. This work was supported by the Natural Scientific Research Fund of Hunan Provincial of China (Grant Nos. 2016JJ6103, 2016JJ6104), and the Construction Program of the Key Discipline in Hunan University of Arts and Science-Applied Mathematics.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yu, Y. Exponential Stability of Pseudo Almost Periodic Solutions for Cellular Neural Networks with Multi-Proportional Delays. Neural Process Lett 45, 141–151 (2017). https://doi.org/10.1007/s11063-016-9516-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-016-9516-z
Keywords
- Cellular neural network
- Pseudo almost periodic solution
- Existence
- Exponential stability
- Multi-proportional delay