Abstract
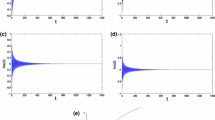
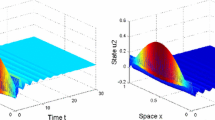
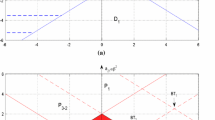
In this paper, a class of delayed complex-valued neural network with diffusion under Dirichlet boundary conditions is considered. By using the properties of the Laplacian operator and separating the neural network into real and imaginary parts, the corresponding characteristic equation of neural network is obtained. Then, the dynamical behaviors including the local stability, the existence of Hopf bifurcation of zero equilibrium are investigated. Furthermore, by using the normal form theory and center manifold theorem of the partial differential equation, the explicit formulae which determine the direction of bifurcations and stability of bifurcating periodic solutions are obtained. Finally, a numerical simulation is carried out to illustrate the results.


Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Hirose A (2012) Complex-valued neural networks. Springer, Berlin
Ding X, Cao J, Zhao X et al (2017) Finite-time stability of fractional-order complex-valued neural networks with time delays. Neural Process Lett 46(2):1–20
Lee DL (2006) Improvements of complex-valued Hopfield associative memory by using generalized projection rules. IEEE Trans Neural Netw 17(5):1341–1347
Gong W, Liang J, Zhang C et al (2016) Nonlinear measure approach for the stability analysis of complex-valued neural networks. Neural Process Lett 44(2):539–554
Nitta T (2003) Solving the XOR problem and the detection of symmetry using a single complex-valued neuron. Neural Netw 16(8):1101–1105
Hu J, Wang J (2012) Global stability of complex-valued recurrent neural networks with time-delays. IEEE Trans Neural Netw Learn Syst 23(6):853–865
Dong T, Liao X, Wang A (2015) Stability and Hopf bifurcation of a complex-valued neural network with two time delays. Nonlinear Dyn 82(1–2):173–184
Wang Z, Huang L (2016) Global stability analysis for delayed complex-valued BAM neural networks. Neurocomputing 173:2083–2089
Song Q, Zhao Z (2016) Stability criterion of complex-valued neural networks with both leakage delay and time-varying delays on time scales. Neurocomputing 171:179–184
Dong T, Liao X (2013) Hopf-Pitchfork bifurcation in a simplified BAM neural network model with multiple delays. J Comput Appl Math 253:222–234
Li Y, Liao X, Li H (2016) Global attracting sets of non-autonomous and complex-valued neural networks with time-varying delays. Neurocomputing 173:994–1000
Dong T, Liao X (2013) Bogdanov–Takens bifurcation in a tri-neuron BAM neural network model with multiple delays. Nonlinear Dyn 71(3):583–595
Wang Z, Huang L (2016) Global stability analysis for delayed complex-valued BAM neural networks. Neurocomputing 173:2083–2089
Xu W, Cao J, Xiao M et al (2015) A new framework for analysis on stability and bifurcation in a class of neural networks with discrete and distributed delays. IEEE Trans Cybern 45(10):2224–2236
Li Y (2017) Impulsive synchronization of stochastic neural networks via controlling partial states. Neural Process Lett 46(1):59–69
Lu J, Wang Z, Cao J et al (2012) Pinning impulsive stabilization of nonlinear dynamical networks with time-varying delay. Int J Bifurc Chaos 22(7):1250176
Zhao H, Yuan J, Zhang X (2015) Stability and bifurcation analysis of reaction–diffusion neural networks with delays. Neurocomputing 147:280–290
Ren SY, Wu J, Wei PC (2017) Passivity and pinning passivity of coupled delayed reaction–diffusion neural networks with Dirichlet boundary conditions. Neural Process Lett 45(3):869–885
Sheng Y, Zeng Z (2017) Synchronization of stochastic reaction–diffusion neural networks with Dirichlet boundary conditions and unbounded delays. Neural Netw 93:89–98
Lu JG (2008) Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos Solitons Fractals 35(1):116–125
Li R, Cao J (2016) Stability analysis of reaction–diffusion uncertain memristive neural networks with time-varying delays and leakage term. Appl Math Comput 278:54–69
Zheng CD, Zhang Y, Wang Z (2014) Stability analysis of stochastic reaction–diffusion neural networks with Markovian switching and time delays in the leakage terms. Int J Mach Learn Cybern 5(1):3–12
Tian X, Xu R, Gan Q (2015) Hopf bifurcation analysis of a BAM neural network with multiple time delays and diffusion. Appl Math Comput 266:909–926
Tian X, Xu R (2017) Stability and Hopf bifurcation of time fractional Cohen–Grossberg neural networks with diffusion and time delays in leakage terms. Neural Process Lett 45(2):593–614
Dong T, Xu W, Liao X (2017) Hopf bifurcation analysis of reaction–diffusion neural oscillator system with excitatory-to-inhibitory connection and time delay. Nonlinear Dyn 89(4):2329–2345
Dong T, Xia L (2017) Stability and Hopf bifurcation of a reaction–diffusion neutral neuron system with time delay. Int J Bifurc Chaos 27(14):1250176
Ruan S, Wei J (2003) On the zeros of transcendental functions with applications to stability of delay differential equations with two delays. Dyn Contin Discrete Impuls Syst Series A 10:863–874
Wu J (2012) Theory and applications of partial functional differential equations. Springer, Berlin
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under Grant 61503310 and 61402381, in part by the supported by the Fundamental Research Funds for the Central Universities under Grant XDJK2017D170 and XDJK2017D183, in part by China Postdoctoral Foundation under Grant 2016M600720, in part by Chongqing Postdoctoral Project under Grant Xm2016003.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Dong, T., Bai, J. & Yang, L. Bifurcation Analysis of Delayed Complex-Valued Neural Network with Diffusions. Neural Process Lett 50, 1019–1033 (2019). https://doi.org/10.1007/s11063-018-9899-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-018-9899-0