Skip to main content
Springer Nature Link
Log in

Sign Normalised Hammerstein Spline Adaptive Filtering Algorithm in an Impulsive Noise Environment

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

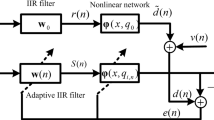
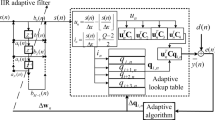
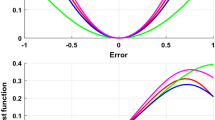
In this paper, a sign normalised least mean square algorithm (SNLMS) based on Hammerstein spline adaptive filter (HSAF) is proposed, which is derived by minimising the absolute value of the a posteriori error. The control points, collected in an adaptive lookup table which is interpolated by a local low-order polynomial spline curve and the tap weights of the linear filter are updated by using the direction information of the a posteriori error. The minimization of the absolute value of the a posteriori error reduces the impact of impulsive noises. The new algorithm is called HSAF-SNLMS and can be used to identify the Hammerstein-type nonlinear systems. Furthermore, the convergence performance analysis is carried out by considering the identification of the Hammerstein-type system and the computational complexity of the proposed algorithm is also analyzed. Simulation results in system identification demonstrate the proposed HSAF-SNLMS obtains more robust performance when compared with the existing spline adaptive filter algorithms in impulsive noise environments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Guerin A, Faucon D, Bouquin-Jeannes RL (2003) Nonlinear acoustic echo cancellation based on Volterra filters. IEEE Trans Speech Audio Process 11(6):672–683

    Article  Google Scholar 

  2. Patel V, George NV (2015) Nonlinear active control using spline adaptive filters. Appl Acoust 93:38–43

    Article  Google Scholar 

  3. Patel V, Gandhi V, Heda S, George NV (2016) Design of adaptive exponential functional link network-based nonlinear filters. IEEE Trans Circuits Syst I Regul Pap 63(9):1434–1442

    Article  MathSciNet  Google Scholar 

  4. Patra JC, Meher PK, Chakraborty G (2009) Nonlinear channel equalization for wireless communication systems using Legendre neural networks. Signal Process 89(11):2251–2262

    Article  MATH  Google Scholar 

  5. Schetzen M (1980) The Volterra and Wiener theories of nonlinear systems. Wiley, New York

    MATH  Google Scholar 

  6. Haykin S (2009) Neural networks and learning machines, 2nd edn. Pearson Publishing, Old Tappan, NJ

    Google Scholar 

  7. Giri F, Bai EW (2010) Block-oriented nonlinear system identification. Springer, Berlin

    Book  MATH  Google Scholar 

  8. Scarpiniti M, Comminiello D, Parisi R, Uncini A (2013) Nonlinear spline adaptive filtering. Signal Process 93(4):772–783

    Article  MATH  Google Scholar 

  9. Scarpiniti M, Comminiello D, Parisi R, Uncini A (2014) Hammerstein uniform cubic spline adaptive filtering: learning and convergence properties. Signal Process 100(7):112–123

    Article  Google Scholar 

  10. Scarpiniti M, Comminiello D, Parisi R, Uncini A (2015) Novel cascade spline architectures for the identification of nonlinear systems. IEEE Trans Circuits Syst I Regul Pap 62(7):1825–1835

    Article  MathSciNet  MATH  Google Scholar 

  11. Bai EW (2003) Frequency domain identification of Wiener models. Automatica 39(9):1521–1530

    Article  MathSciNet  MATH  Google Scholar 

  12. Bai EW, Fu M (2002) A blind approach to Hammerstein model identification. IEEE Trans Signal Process 50(7):1610–1619

    Article  Google Scholar 

  13. Ljung L (2006) Identification of nonlinear systems. In: 9th International conference on control, automation, robotics and vision (ICARCV), vol 1, pp 9–14

  14. Shao T, Zheng YR, Benesty J (2010) An affine projection sign algorithm robust against impulsive interferences. IEEE Signal Process Lett 17(4):327–330

    Article  Google Scholar 

  15. Kim JH, Chang JH, Nam SW (2013) Sign subband adaptive filter with L1Cnorm minimisation-based variable step-size. Electron Lett 49(21):1325–1326

    Article  Google Scholar 

  16. Ni J, Chen X, Yang J (2014) Two variants of the sign subband adaptive filter with improved convergence rate. Signal Process 96(5):325–331

    Article  Google Scholar 

  17. Wen P, Zhang S, Zhang J (2016) A novel subband adaptive filter algorithm against impulseive noise and its performance analysis. Signal Process 127(C):282–287

  18. Wen P, Zhang J (2017) Robust variable step-size sign subband adaptive filter algorithm against impulseive noise. Signal Process 139:110–115

    Article  Google Scholar 

  19. Bhotto ZA, Antoniou A (2013) A family of shrinkage adaptive-filtering algorithms. IEEE Trans Signal Process 61(7):1689–1697

    Article  MathSciNet  MATH  Google Scholar 

  20. Zhang S, Zhang J, Han H (2017) Robust shrinkage normalized sign algorithm in an impulsive noise environment. IEEE Trans Circuits Syst II Express Br 64(1):91–95

    Article  MathSciNet  Google Scholar 

  21. Guan S, Li Z (2017) Normalised spline adaptive filtering algorithm for nonlinear system identification. Neural Process Lett 5:1–13

    Google Scholar 

  22. Scarpiniti M, Comminiello D, Parisi R, Scarano G, Parisi R, Uncini A (2016) Steady-state performance of spline adaptive filters. IEEE Trans Signal Process 64(4):816–828

    Article  MathSciNet  MATH  Google Scholar 

  23. George NV, Panda G (2012) A robust filtered-s LMS algorithm for nonlinear active noise control. Appl Acoust 73(8):836–841

    Article  Google Scholar 

  24. Lu L, Zhao H (2017) Active impulsive noise control using maximum correntropy with adaptive kernel size. Mech Syst Signal Process 87:180–191

    Article  Google Scholar 

  25. Kurian NC, Patel K, George NV (2017) Robust active noise control: an information theoretic learning approach. Appl Acoust 117:180–184

    Article  Google Scholar 

Download references

Acknowledgements

This research was supported by the National Natural Science Foundation of China under Grant 61501119.

Author information

Authors and Affiliations

  1. School of Electronic Engineering, Dongguan University of Techonology, No.1 DaXue Road, Dong’guan, 523808, Guangdong, China

    Chang Liu, Zhi Zhang & Xiao Tang

Authors
  1. Chang Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhi Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xiao Tang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chang Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, C., Zhang, Z. & Tang, X. Sign Normalised Hammerstein Spline Adaptive Filtering Algorithm in an Impulsive Noise Environment. Neural Process Lett 50, 477–496 (2019). https://doi.org/10.1007/s11063-019-09996-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-019-09996-6

Keywords