Abstract
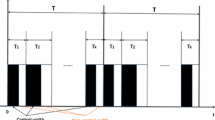
In the literature, a lot of work focused on studying intermittent control problems via feedback control strategy. No study on the intermittent control problems via sliding mode control method has been reported so far. This paper studies the problem of fast synchronization between two complex dynamical networks via aperiodically intermittent control and sliding mode control. In order to achieve fast synchronization of complex dynamical networks by using aperiodically intermittent sliding mode controller, new differential inequalities are derived firstly. After that, some sufficient finite-time synchronization criteria and finite-time achieving slide mode surface are obtained based on finite-time stability theory, aperiodically intermittent sliding mode control technique and constructing Lyapunov function. Finally, an example is provided to verify the effectiveness of the proposed theoretical methods.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Strogatz SH (2001) Exploring complex networks. Nature 410:268–276
Newman MEJ (2003) The structure and function of complex networks. SIAM Rev 45:167–256
Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D-U (2006) Complex networks: structure and dynamics. Phys Rep 424:175–308
Suykens JAK, Osipov GV (2008) Introduction to focus issue: synchronization in complex networks. Chaos 18:037101
Mei J, Jiang M, Huang Z (2011) Outer synchronization between two complex networks with identical and nonidentical topological structures. In: 2011 fourth international workshop on advanced computational intelligence (IWACI), pp 757–762
Al-mahbashi G, Noorani MS, Bakar SA, Vahedi S (2016) Adaptive projective lag synchronization of uncertain complex dynamical networks with disturbance. Neurocomputing 207:645–652
Hu J, Zeng C (2017) Adaptive exponential synchronization of complex-valued Cohen–Grossberg neural networks with known and unknown parameters. Neural Netw 86:90–101
Xu Y, Zhang J, Zhou W, Tong D (2017) Adaptive synchronization of complex dynamical networks with bounded delay feedback controller. Optik Int J Light Electron Opt 131:467–474
Liu Y, Zhu C, Chu D, Li W (2018) Synchronization of stochastic coupled systems with time-varying coupling structure on networks via discrete-time state feedback control. Neurocomputing 285:104–116
Xu M, Wang J, Huang Y, Wei P, Wang S (2017) Pinning synchronization of complex dynamical networks with and without time-varying delay. Neurocomputing 266:263–273
Ma Y, Ma N, Chen L (2018) Synchronization criteria for singular complex networks with Markovian jump and time-varying delays via pinning control. Nonlinear Anal Hybrid Syst 29:85–99
Zheng S (2017) Pinning and impulsive synchronization control of complex dynamical networks with non-derivative and derivative coupling. J Frankl Inst 354(14):6341–6363
Yang X, Lu J, Ho DWC, Song Q (2018) Synchronization of uncertain hybrid switching and impulsive complex networks. Appl Math Model 59:379–392
Zhang H, Wang X, Lin X (2016) Synchronization of complex-valued neural network with sliding mode control. J Frankl Inst 353(2):345–358
Ali MS, Yogambigai J, Cao J (2017) Synchronization of master–slave Markovian switching complex dynamical networks with time-varying delays in nonlinear function via sliding mode control. Acta Math Sci 37(2):368–384
Huang J, Li C, Han Q (2009) Stabilization of delayed chaotic neural networks by periodically intermittent control. Circuits Syst Signal Process 28:567–579
Mei J, Jiang M, Wang B, Liu Q, Xu W, Liao T (2014) Exonential p-Synchronization of non-autonomous Cohen–Grossberg neural networks with reaction–diffusion terms via periodically intermittent control. Neural Process Lett 40:103–126
Liu X, Li P, Chen T (2015) Cluster synchronization for delayed complex networks via periodically intermittent pinning control. Neurocomputing 162:191–200
Zhang Z, He Y, Zhang C, Wu M (2016) Exponential stabilization of neural networks with time-varying delay by periodically intermittent control. Neurocomputing 207:469–475
Chen W, Zhong J, Zheng W (2016) Delay-independent stabilization of a class of time-delay systems via periodically intermittent control. Automatica 71:89–97
Ma X, Wang J (2016) Pinning outer synchronization between two delayed complex networks with nonlinear coupling via adaptive periodically intermittent control. Neurocomputing 199:197–203
Feng J, Yang P, Zhao Y (2016) Cluster synchronization for nonlinearly time-varying delayed coupling complex networks with stochastic perturbation via periodically intermittent pinning control. Appl Math Comput 291:52–68
Yang S, Li C, Huang T (2016) Exponential stabilization and synchronization for fuzzy model of memristive neural networks by periodically intermittent control. Neural Netw 75:162–172
Wang Q, He Y, Tan G, Wu M (2017) Observer-based periodically intermittent control for linear systems via piecewise Lyapunov function method. Appl Math Comput 293:438–447
Li H, Hu C, Jiang H, Teng Z, Jiang Y (2017) Synchronization of fractional-order complex dynamical networks via periodically intermittent pinning control. Chaos Solitons Fractals 103:357–363
Wang P, Hong Y, Su H (2018) Stabilization of stochastic complex-valued coupled delayed systems with Markovian switching via periodically intermittent control. Nonlinear Anal Hybrid Syst 29:395–413
Guo B, Xiao Y, Zhang C (2018) Synchronization analysis of stochastic coupled systems with time delay on networks by periodically intermittent control and graph-theoretic method. Nonlinear Anal Hybrid Syst 30:118–133
Zhang W, Li C, Huang T, Xiao M (2015) Synchronization of neural networks with stochastic perturbation via aperiodically intermittent control. Neural Netw 71:105–111
Liu M, Jiang H, Hu C (2016) Synchronization of hybrid-coupled delayed dynamical networks via aperiodically intermittent pinning control. J Frankl Inst 353(12):2722–2742
Liu X, Liu Y, Zhou L (2016) Quasi-synchronization of nonlinear coupled chaotic systems via aperiodically intermittent pinning control. Neurocomputing 173:759–767
Liu X, Chen Z, Zhou L (2017) Synchronization of coupled reaction–diffusion neural networks with hybrid coupling via aperiodically intermittent pinning control. J Frankl Inst 354(15):7053–7076
Lei X, Cai S, Jiang S, Liu Z (2017) Adaptive outer synchronization between two complex delayed dynamical networks via aperiodically intermittent pinning control. Neurocomputing 222:26–35
Wang J (2017) Synchronization of delayed complex dynamical network with hybrid-coupling via aperiodically intermittent pinning control. J Frankl Inst 354(4):1833–1855
Wu X, Feng J, Nie Z (2018) Pinning complex-valued complex network via aperiodically intermittent control. Neurocomputing 305:70–77
Zhou P, Cai S, Jiang S, Liu Z (2018) Exponential cluster synchronization in directed community networks via adaptive nonperiodically intermittent pinning control. Physica A 492:1267–1280
Zhang D, Mei J, Miao P (2017) Global finite-time synchronization of different dimensional chaotic systems. Appl Math Model 48:303–315
Ren H, Deng F, Peng Y (2018) Finite time synchronization of Markovian jumping stochastic complex dynamical systems with mix delays via hybrid control strategy. Neurocomputing 272:683–693
Qiu S, Huang Y, Ren S (2018) Finite-time synchronization of multi-weighted complex dynamical networks with and without coupling delay. Neurocomputing 275:1250–1260
Mei J, Jiang M, Xu W, Wang B (2013) Finite-time synchronization control of complex dynamical networks with time delay. Commun Nonlinear Sci Numer Simulat 18:2462–2478
Mei J, Jiang M, Wang X, Han J, Wang S (2014) Finite-time synchronization of drive-response systems via periodically intermittent adaptive control. J Frankl Inst 351:2691–2710
Mei J, Jiang M, Wu Z, Wang X (2014) Periodically intermittent controlling for finite-time synchronization of complex dynamical networks. Nonlinear Dyn 79:295–305
Yang F, Mei J, Wu Z (2016) Finite-time synchronisation of neural networks with discrete and distributed delays via periodically intermittent memory feedback control. IET Control Theory Appl 10:1630–1640
Zhao H, Li L, Xiao J, Yang Y, Zheng M (2017) Parameters tracking identification based on finite-time synchronization for multi-links complex network via periodically switch control. Chaos Solitons Fractals 104:268–281
Cheng L, Yang Y, Li L, Sui X (2018) Finite-time hybrid projective synchronization of the drive-response complex networks with distributed-delay via adaptive intermittent control. Physica A 500:273–286
Liu M, Jiang H, Hu C (2017) Finite-time synchronization of delayed dynamical networks via aperiodically intermittent control. J Frankl Inst 354(13):5374–5397
Zhang D, Shen Y, Mei J (2017) Finite-time synchronization of multi-layer nonlinear coupled complex networks via intermittent feedback control. Neurocomputing 225:129–138
Mei J, Jiang M, Wang J (2013) Finite-time structure identification and synchronization of drive-response systems with uncertain parameter. Commun Nonlinear Sci Numer Simulat 18:999–1015
Fan Y, Liu H, Zhu Y, Mei J (2016) Fast synchronization of complex dynamical networks with time-varying delay via periodically intermittent control. Neurocomputing 205:182–194
Liu X, Chen T (2015) Synchronization of linearly coupled networks with delays via aperiodically intermittent pinning control. IEEE Trans Neural Netw Learn Syst 26(10):2396–2407
Zhang G, Shen Y (2015) Exponential stabilization of memristor-based chaotic neural networks with time-varying delays via intermittent control. IEEE Trans Neural Netw Learn Syst 26:1431–1441
Kang Y, Qin J, Ma Q, Gao H, Zheng W (2018) Cluster synchronization for interacting clusters of nonidentical nodes via intermittent pinning control. IEEE Trans Neural Netw Learn Syst 29(5):1747–1759
Hu C, Yu J (2016) Generalized intermittent control and its adaptive strategy on stabilization and synchronization of chaotic systems. Chaos Solitons Fractals 91:262–269
Guan Z, Yue D, Hu B, Li T, Liu F (2017) Cluster synchronization of coupled genetic regulatory networks with delays via aperiodically adaptive intermittent control. IEEE Trans Nanobiosci 16(7):585–599
Hu A, Cao J (2017) Consensus of multi-agent systems via intermittent event-triggered control. Int J Syst Sci 48(2):280–287
Xiong W, Patel R, Cao J, Zheng WX (2017) Synchronization of hierarchical time-varying neural networks based on asynchronous and intermittent sampled-data control. IEEE Trans Neural Netw Learn Syst 28(11):2837–2843
Zheng S (2016) Intermittent impulsive projective synchronization in time-varying delayed dynamical network with variable structures. Complexity 21:547–556
Acknowledgements
The authors would like to thank the editor and the anonymous reviewers for their valuable comments and constructive suggestions. This research is supported by National Natural Science Foundation of China (Grant Nos. 11771172, 11871305, 61903149, 61907021), Humanity and Social Science foundation of MOE of China (20171304).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Lemma 4
Take \(M_0=V^{1-\eta }(0)+\frac{\alpha }{p_1}\) and \(W(t)=V^{1-\eta }(t)\text{ exp }\{(1-\eta )p_1t\}\), where \(t\ge 0\). Let \(Q(t)=W(t)-M_0+\frac{\alpha }{p_1}\text{ exp }\{(1-\eta )p_1t\}\).
It will be proven in the following parts that
for all \(t \in [0,s_0)\). Otherwise, there is a \(a_0\in [0,s_0)\), to make that
With Eqs. (55), (56) and (57), one can obtain
which contradicts the second inequality in (56). Hence, (55) holds.
Let \(W_1(t)=V^{1-\eta }(t)e^{(1-\eta )p_1t}e^{-(1-\eta )p_1(t-s_0)}e^{-(1-\eta )p_2(t-s_0)}\), and \(H(t)=W_1(t)-M_0+\frac{\alpha }{p_1}e^{(1-\eta )p_1t}e^{-(1-\eta )p_1(t-s_0)}e^{-(1-\eta )p_2(t-s_0)},~t\ge s_0\) and prove that
for \(t\in [s_0,t_1)\). Otherwise, there exists a \(a_1 \in [s_0,t_1)\) such that
According to Eqs. (60) and (61),
which contradicts the second inequality in (60). Hence (59) holds. From (59), it is easy to see that
Consequently,
for \(t\in [\theta T,T)\).
On the other hand, together with (55), one can obtain
Therefore,
for all \(~t\in [0,t_1)\).
Furthermore, it can be proved that
for \(t \in [t_1,s_1)\). Otherwise, there is a \(a_2 \in [t_1,s_1)\) to make that
where \(\widetilde{Q}(t)=W(t)- e^{(1-\eta )(p_1+p_2)(t_1-s_0)}\Big [M_0-\frac{\alpha }{p_1}e^{(1-\eta )p_1t}e^{-(1-\eta )(p_1+p_2)(t_1-s_0)}\Big ]\).
Similar to (58), one has
which contradicts the second inequality in (65). Hence, (64)holds.
With the same approach, one can prove that
for \(t\in [s_1,t_2)\).
With induction method, the following estimation of W(t) for any m can be derived.
For \(t_m \le t <s_m\),
and for \(s_m\le t<t_{m+1}\),
As there is a nonnegative integer m such that \(t_m\le t<t_{m+1}\) for any \(t\ge 0\), the following estimation of W(t) for any t can be deduced by Eqs. (66) and (67).
For \(t_m\le t<s_m\), and according to Definition 2, one has
For \(s_m\le t<t_{m+1}\), and with Lemma 3, one can obtain
According to the definition of W(t), one obtains
The proof is completed. \(\square \)
Proof of Lemma 5
Take \(M_0=V^{1-\eta }(0)\) and \(W(t)=V^{1-\eta }(t)+\alpha {(1-\eta )t}\). Let \(Q(t)=W(t)-M_0\).
In the following, we will prove that
for all \(t \in [0,s_0)\). Otherwise, there is a \(a_0\in [0,s_0)\), to make that
For \(\forall ~t \in [0,s_0)\), one can obtain
which contradicts the second inequality in (69). Hence, (68) holds.
Let \(H(t)=W(t)-M_0-\alpha (1-\eta )(t-s_0)\). Next, we prove that for \(t\in [s_0,t_1)\)
For \(\forall ~t \in [s_0,t_1)\), one can get
This is to say that H(t) is decreasing in \((s_0,t_1)\). Hence,
Hence, Eq. (72) holds.
On the other hand, together with (68), one can obtain
for \(t\in [0,t_1)\).
Similarly, with the same approach of Eq. (71), one can prove that: for \(t\in [t_1,s_1)\),
Let \(Q_1(t)=W(t)-M_0-\alpha (1-\eta )(t_1-s_0)\), it is obtained that \(\dot{Q}_1(t)\le 0\), for \(t\in [t_1,s_1)\). Similar to the proof of Eq. (72), one can verify
for \(t\in [s_1,t_2)\). Take \(H_1(t)=W(t)-M_0+\alpha (1-\eta )(t_1-s_0)-\alpha (1-\eta )(t-t_1)\). Then, one can easy obtain that \(\dot{H}_1(t)\le 0\), for \(t\in [s_1,t_2)\).
With induction method, one can derive the following estimation of W(t) for any integer m.
For \(t_m\le t<s_m\),
and for \(s_m\le t<t_{m+1}\),
Since for any \(t\ge 0\), there exists a nonnegative integer m, such that \(t_m\le t<t_{m+1}\) for any \(t\ge 0\), the following estimation of W(t) for any t can be deduced by Eqs. (74) and (75).
For \(t_m\le t<s_m\), and according to Definition 2, one has
For \(s_m\le t<t_{m+1}\), and with Lemma 3, one can obtain
According to the definition of W(t), one obtains
The proof is completed. \(\square \)
Rights and permissions
About this article
Cite this article
Fan, Y., Mei, J., Liu, H. et al. Fast Synchronization of Complex Networks via Aperiodically Intermittent Sliding Mode Control. Neural Process Lett 51, 1331–1352 (2020). https://doi.org/10.1007/s11063-019-10145-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-019-10145-2