Skip to main content
Springer Nature Link
Log in

A New Lyapunov Function Method to the Fixed-Time Cluster Synchronization of Directed Community Networks

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

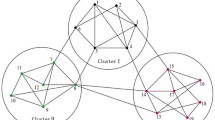
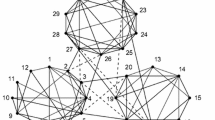
In this paper, the issue of fixed-time cluster synchronization is investigated for the directed community networks. We propose a new Lyapunov function method which leads to the settling time is not only independent of the initial value, but also unrelated to the number and dimensions of nodes in the networks. This means our estimated settling time is more accurate and much tighter than the one in the existing results. By designing the corresponding controllers and using the fixed-time stability theorem, some new criteria are derived to guarantee that the community networks achieve cluster synchronization in fixed time. Finally, an illustrative example with computer simulations is given to verify the theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Girvan M, Newman MEJ (2002) Community structure in social and biological networks. Proc Natl Acad Sci USA 99(12):7821–7826

    Article  MathSciNet  Google Scholar 

  2. Newman MEJ (2003) The structure and function of complex networks. SIAM Rev 45(2):167–256

    Article  MathSciNet  Google Scholar 

  3. Fortunato S (2010) Community detection in graphs. Phys Rep 486:75–174

    Article  MathSciNet  Google Scholar 

  4. Benson AR, Gleich DF, Leskovec J (2016) Higher-order organization of complex networks. Science 353:163–166

    Article  Google Scholar 

  5. Nie X, Zheng W (2015) Multistability and instability of neural networks with discontinuous nonmonotonic piecewise linear activation functions. IEEE Trans Neural Netw Learn Syst 26(11):2901–2913

    Article  MathSciNet  Google Scholar 

  6. Nie X, Zheng W (2016) Dynamical behaviors of multiple equilibria in competitive neural networks with discontinuous nonmonotonic piecewise linear activation functions. IEEE Trans Cybern 46(3):679–693

    Article  Google Scholar 

  7. Nie X, Liang J, Cao J (2019) Multistability analysis of competitive neural networks with Gaussian-wavelet-type activation functions and unbounded time-varying delays. Appl Math Comput 356:449–468

    MathSciNet  MATH  Google Scholar 

  8. Wu X, Bao H (2020) Finite time complete synchronization for fractional-order multiplex networks. Appl Math Comput 377:125188

    Article  MathSciNet  Google Scholar 

  9. Shi J, Zeng Z (2020) Global exponential stabilization and lag synchronization control of inertial neural networks with time delays. Neural Netw 126:11–20

    Article  Google Scholar 

  10. Zhao L, Wang J (2020) Lag \(H_\infty \) synchronization and lag synchronization for multiple derivative coupled complex networks. Neurocomputing 384:46–56

    Article  Google Scholar 

  11. Liu P, Zeng Z, Wang J (2020) Asymptotic and finite-time cluster synchronization of coupled fractional-order neural networks with time delay. IEEE Trans Neural Netw Learn Syst 31(11):4956–4967

    Article  MathSciNet  Google Scholar 

  12. Chen H, Shi P, Lim C (2019) Cluster synchronization for neutral stochastic delay networks via intermittent adaptive control. IEEE Trans Neural Netw Learn Syst 30(11):3246–3259

    Article  MathSciNet  Google Scholar 

  13. Wang K, Fu X, Li K (2009) Cluster synchronization in community networks with nonidentical nodes. Chaos 19(2):023106

    Article  MathSciNet  Google Scholar 

  14. Kaneko K (1994) Relevance of dynamic clustering to biological networks. Physica D 75:55–73

    Article  Google Scholar 

  15. Schnitzler A, Gross J (2005) Normal and pathological oscillatory communication in the brain. Nat Rev Neurosci 6(4):285–296

    Article  Google Scholar 

  16. Shi L, Zhu H, Zhong S, Shi K, Cheng J (2017) Cluster synchronization of linearly coupled complex networks via linear and adaptive feedback pinning controls. Nonlinear Dyn 88(2):859–870

    Article  Google Scholar 

  17. Liu L, Zhou W, Li X, Sun Y (2019) Dynamic event-triggered approach for cluster synchronization of complex dynamical networks with switching via pinning control. Neurocomputing 340:32–41

    Article  Google Scholar 

  18. Yang W, Wang Y, Shen Y, Pan L (2021) Cluster synchronization of delayed coupled neural networks: delay-dependent distributed impulsive control. Neural Netw 142:34–43

    Article  Google Scholar 

  19. Haimo VT (1986) Finite time controllers. SIAM J Control Optim 24(4):760–770

    Article  MathSciNet  Google Scholar 

  20. Tang R, Su H, Zou Y, Yang X (2021) Finite-time synchronization of Markovian coupled neural networks with delays via intermittent quantized control: Linear programming approach. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2021.3069926

    Article  Google Scholar 

  21. Zhou Y, Wan X, Huang C, Yang X (2020) Finite-time stochastic synchronization of dynamic networks with nonlinear coupling strength via quantized intermittent control. Appl Math Comput 376:125157

    MathSciNet  MATH  Google Scholar 

  22. Zou Y, Su H, Tang R, Yang X (2021) Finite-time bipartite synchronization of switched competitive neural networks with time delay via quantized control. ISA Trans. https://doi.org/10.1016/j.isatra.2021.06.015

    Article  Google Scholar 

  23. Polyakov A (2012) Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans Automat Contr 57(8):2106–2110

    Article  MathSciNet  Google Scholar 

  24. Haliding X, Jiang H, Abdurahman A, Hu C (2020) Fixed-time lag synchronization analysis for delayed memristor-based neural networks. Neural Process Lett 52(1):485–509

    Article  Google Scholar 

  25. Zhang W, Yang X, Yang S, Huang C, Alsaadi FE (2021) Fixed-time control of competitive complex networks. Neural Comput Appl 33(13):7943–7951

    Article  Google Scholar 

  26. Zhang W, Yang X, Yang S, Alsaedi A (2021) Finite-time and fixed-time bipartite synchronization of complex networks with signed graphs. Math Comput Simulat. https://doi.org/10.1016/j.matcom.2021.04.013

    Article  MathSciNet  MATH  Google Scholar 

  27. Long C, Zhang G, Hu J (2021) Fixed-time synchronization for delayed inertial complex-valued neural networks. Appl Math Comput 405:126272

    MathSciNet  MATH  Google Scholar 

  28. Xu D, Yang X, Tang R (2020) Finite-time and fixed-time non-chattering control for inertial neural networks with discontinuous activations and proportional delay. Neural Process Lett 51(3):2337–2353

    Article  Google Scholar 

  29. Gan Q, Xiao F, Qin Y, Yang J (2019) Fixed-time cluster synchronization of discontinuous directed community networks via periodically or aperiodically switching control. IEEE Access 7:83306–83318

    Article  Google Scholar 

  30. Cai S, Zhou F, He Q (2019) Fixed-time cluster lag synchronization in directed heterogeneous community networks. Physica A 525:128–142

    Article  MathSciNet  Google Scholar 

  31. Jiang S, Qi Y, Cai S, Lu X (2021) Light fixed-time control for cluster synchronization of complex networks. Neurocomputing 424:63–70

    Article  Google Scholar 

  32. Zhou F, Zhao Y, Cai S (2019) Fixed-time cluster synchronization in directed community networks with diverse coupling and different-order nodes. Int J Mod Phys B 33(8):1950059

    Article  MathSciNet  Google Scholar 

  33. Yang L, Jiang J, Liu X (2016) Cluster synchronization in community network with hybrid coupling. Chaos Solitons Fract 86:82–91

    Article  MathSciNet  Google Scholar 

  34. Zhou P, Cai S, Shen J, Liu Z (2018) Adaptive exponential cluster synchronization in colored community networks via aperiodically intermittent pinning control. Nonlinear Dyn 92(3):905–921

    Article  Google Scholar 

  35. Wu Z (2014) Cluster synchronization in colored community network with different order node dynamics. Commun Nonlinear Sci Numer Simul 19(4):1079–1087

    Article  MathSciNet  Google Scholar 

  36. Hardy GH, Littlewood JE, Pólya G (1952) Inequalities. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  37. Hu C, Yu J, Chen Z, Jiang H, Huang T (2017) Fixed-time stability of dynamical systems and fixed-time synchronization of coupled discontinuous neural networks. Neural Netw 89:74–83

    Article  Google Scholar 

  38. Yang X, Lam J, Daniel WC, Feng Z (2017) Fixed-time synchronization of complex networks with impulsive effects via nonchattering control. IEEE Trans Automat Contr 62(11):5511–5521

    Article  MathSciNet  Google Scholar 

  39. Chen C, Li L, Peng H, Yang Y, Mi L, Zhao H (2020) A new fixed-time stability theorem and its application to the fixed-time synchronization of neural networks. Neural Netw 123:412–419

    Article  Google Scholar 

  40. Liu X, Chen T (2011) Cluster synchronization in directed networks via intermittent pinning control. IEEE Trans Neural Netw 22(7):1009–1020

    Article  Google Scholar 

Download references

Acknowledgements

This work was jointly supported by the National Natural Science Foundation of China under Grant No. 61673111, the National Key Research and Development Program of China under Grant No. 2018AAA0100202, and the Fundamental Research Funds for the Central Universities under Grant No. 2242021k10007.

Author information

Authors and Affiliations

  1. The Jiangsu Provincial Key Laboratory of Networked Collective Intelligence, and School of Mathematics, Southeast University, Nanjing, 211189, China

    Feilong Zhou & Xiaobing Nie

Authors
  1. Feilong Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaobing Nie
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xiaobing Nie.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, F., Nie, X. A New Lyapunov Function Method to the Fixed-Time Cluster Synchronization of Directed Community Networks. Neural Process Lett 54, 2143–2164 (2022). https://doi.org/10.1007/s11063-021-10723-3

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-021-10723-3

Keywords