Observer-based Adaptive Funnel Dynamic Surface Control for Nonlinear Systems with Unknown Control Coefficients and Hysteresis Input

Abstract

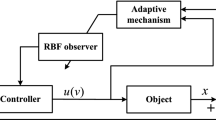
This article investigates an adaptive funnel dynamic surface control (DSC) problem for a class of strict-feedback uncertain nonlinear systems with unknown control coefficients and backlash-like hysteresis input. First, a neural network (NN) state observer is constructed to estimate the unmeasurable states. Second, by utilizing the approximation ability of the radial basis function-neural networks (RBF-NNs) and the backstepping control technique, an adaptive tracking control scheme is developed, which can guarantee that all closed-loop signals are semi-globally uniformly ultimately bounded (SGUUB). Meanwhile, the DSC technique is introduced to avoid the complexity problem in the process of backstepping control. Third, by employing the funnel control (FC), the tracking error remains in a predefined funnel and converges to a prescribed interval via using a new funnel function. Finally, the superiority of the developed controller is validated by two examples.

Appendices

Appendix 1

Then, the derivative of $V_0$ yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_0=\;&{\dot{e}}^{\mathrm {T}}Pe+e^{\mathrm {T}}P{\dot{e}} =e^{\mathrm {T}}(A_1^{\mathrm {T}}P+PA_1)e\\&+2e^{\mathrm {T}}P(\triangle f +\xi +\varXi +d+\triangle g). \end{aligned} \end{aligned}$$

(32)

By using Lemma 1, Assumptions 2 and 4, we have

$$\begin{aligned} 2e^{\mathrm {T}}P\xi\le & {} \Vert e\Vert ^2+\Vert P\Vert ^2\Vert \xi _i^*\Vert ^2, \end{aligned}$$

(33)

$$\begin{aligned} 2e^{\mathrm {T}}P\varXi\le & {} \Vert e\Vert ^2+\Vert P\Vert ^2 \sum _{i=1}^{n}{\tilde{W}}_i^{\mathrm {T}}{\tilde{W}}_i, \end{aligned}$$

(34)

$$\begin{aligned} 2e^{\mathrm {T}}PD\le & {} \Vert e\Vert ^2+\Vert P\Vert ^2\Vert d_i^*\Vert ^{2}, \end{aligned}$$

(35)

$$\begin{aligned} 2e^{\mathrm {T}}P\triangle f\le & {} \Vert e\Vert ^2+\Vert P\Vert ^2\Vert \triangle f\Vert ^{2}\nonumber \\\le & {} \Vert e\Vert ^2+\Vert P\Vert ^2\sum _{i=2}^{n}Q_i^2\Vert e\Vert ^2, \end{aligned}$$

(36)

$$\begin{aligned} 2e^{\mathrm {T}}P\triangle g\le & {} \Vert e\Vert ^2+\sum _{i=1}^{n-1}m_i{\hat{x}}_{i+1}^2, \end{aligned}$$

(37)

where $m_i=\Vert P\Vert ^2|g_i-g_{i,0}|^2$.

Appendix 2

Step 1: From (10), (13) and (14), the derivative of $z_1$ is given as

$$\begin{aligned} \begin{aligned} {\dot{z}}_1=&\frac{\dot{\omega _1}}{\sqrt{F_{\varPsi }^2-\omega _1^2}}- \frac{\omega _1}{(F_{\varPsi }^2-\omega _1^2)^{\frac{3}{2}}}(F_{\varPsi }{\dot{F}}_{\varPsi }-\omega _1\dot{\omega _1})\\ =&\frac{F_{\varPsi }^2}{\sqrt{(F_{\varPsi }^2-\omega _1^2)^3}}(\dot{\omega _1}-\frac{\omega _1{\dot{F}}_{\varPsi }}{F_{\varPsi }})\\ =&\varPi _1({\dot{x}}_1-{\dot{y}}_d-\frac{\omega _1{\dot{F}}_{\varPsi }}{F_{\varPsi }})\\ =&\varPi _1(g_1x_2+f_1(x_1)+d_1-{\dot{y}}_d-\frac{\omega _1{\dot{F}}_{\varPsi }}{F_{\varPsi }})\\ =&\varPi _1(g_1({\hat{x}}_2+e_2)+f_1(x_1)+d_1-{\dot{y}}_d-\frac{\omega _1{\dot{F}}_{\varPsi }}{F_{\varPsi }}), \end{aligned} \end{aligned}$$

(38)

where $\varPi _1=\frac{F_{\varPsi }^2}{\sqrt{(F_{\varPsi }^2-\omega _1^2)^3}}$.

Choose a Lyapunov function as

$$\begin{aligned} V_1=V_0+\frac{1}{2}z_1^2+\frac{1}{2}\varrho _2^2+\frac{g_1}{2\epsilon _1}{\tilde{\varTheta }}_1^2 +\frac{\iota _1}{2\eta _1}{\tilde{W}}_1^{{\mathrm {T}}}{\tilde{W}}_1, \end{aligned}$$

(39)

where $\iota _1$, $\eta _1$ and $\epsilon _1$ are positive parameters. ${\tilde{\varTheta }}_1=\varTheta _1^*-\varTheta _1$, and $\varTheta _1$ is the estimation of $\varTheta _1^*$, and ${\tilde{W}}_1=W_1^*-W_1$.

Then, the derivative of $V_1$ is calculated as follows

$$\begin{aligned} \begin{aligned} {\dot{V}}_1=&{\dot{V}}_0+z_1{\dot{z}}_1+\varrho _2{\dot{\varrho }}_2 -\frac{g_1}{\epsilon _1}{\tilde{\varTheta }}_1{\dot{\varTheta }}_1 -\frac{\iota _1}{\eta _1}{\tilde{W}}_1^{{\mathrm {T}}}{\dot{W}}_1\\ \le&-\lambda _0\Vert e\Vert ^2+\Vert P\Vert ^2\sum _{i=1}^{n}{\tilde{W}}_i^{\mathrm {T}}{\tilde{W}}_i+\varPhi _0+\sum _{i=1}^{n-1}m_i{\hat{x}}_{i+1}^2\\&-\frac{g_1}{\epsilon _1}{\tilde{\varTheta }}_1{\dot{\varTheta }}_1 -\frac{\iota _1}{\eta _1}{\tilde{W}}_1^{{\mathrm {T}}}{\dot{W}}_1+\varPi _1z_1(g_1e_2+d_1)\\&+\varrho _2{\dot{\varrho }}_2 +z_1\varPi _1\left( g_1{\hat{x}}_2+(W_1^*)^{\mathrm {T}}\varphi _1(x_1)+\xi _1(x_1)-{\dot{y}}_d-\frac{\omega _1{\dot{F}}_{\varPsi }}{F_{\varPsi }}\right) . \end{aligned} \end{aligned}$$

(40)

According to Lemma 1, one has

$$\begin{aligned} \begin{aligned} \varPi _1z_1g_1e_2\le&\frac{1}{2}g_1^2\varPi _1^2z_1^2+\frac{1}{2}\Vert e\Vert ^2,\\ \varPi _1z_1d_1\le&\frac{1}{2}\varPi _1^2z_1^2+\frac{1}{2}(d_1^*)^{2}. \end{aligned} \end{aligned}$$

(41)

Substituting (41), $z_2={\hat{x}}_2-H_2$ into (40) and defining $\varrho _2=H_2-\alpha _1$, it yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_1\le&-(\lambda _0-\frac{1}{2})\Vert e\Vert ^2+\Vert P\Vert ^2\sum _{i=1}^{n}{\tilde{W}}_i^{\mathrm {T}}{\tilde{W}}_i+\varPhi _0\\&+\sum _{i=1}^{n-1}m_i{\hat{x}}_{i+1}^2-\frac{g_1}{\epsilon _1}{\tilde{\varTheta }}_1{\dot{\varTheta }}_1 -\frac{\iota _1}{\eta _1}{\tilde{W}}_1^{\mathrm {T}}{\dot{W}}_1 +\varrho _2{\dot{\varrho }}_2\\&+g_1\varPi _1z_1(z_2+\varrho _2+\alpha _1)+z_1F_1-\frac{g_1^2}{2}\varPi _1^2z_1^2\\&+z_1\varPi _1{\tilde{W}}_1^{{\mathrm {T}}}\varphi _1(x_1) -z_1^2\sum _{l=1}^{n-1}q_{l1}(z_1)+\frac{1}{2}(d_1^*)^{2}, \end{aligned} \end{aligned}$$

(42)

where

$$\begin{aligned} \begin{aligned} F_1(x_1, z_1, {\dot{y}}_d)=&\varPi _1(g_1^2\varPi _1z_1+\frac{1}{2}\varPi _1z_1+W_1^{\mathrm {T}}\varphi _1(x_1)\\&+\xi _1(x_1)-\frac{\omega _1{\dot{F}}_{\varPsi }}{F_{\varPsi }}-{\dot{y}}_d)+z_1\sum _{l=1}^{n-1}q_{l1}(z_1). \end{aligned} \end{aligned}$$

Applying the RBF-NNs $\theta _1^{\mathrm {T}}S_1(Z_1)$ to approximate the packaged function $F_1$, we can obtain

$$\begin{aligned} F_1=\theta _1^{\mathrm {T}}S_1(Z_1)+\sigma _1(Z_1),~|\sigma _1|\le \sigma _1^* \end{aligned}$$

(43)

where $Z_1=(x_1, z_1, {\dot{y}}_d)$. $\sigma _1$ denotes the estimation error and $\sigma _1^*>0$ is an arbitrarily small estimation accuracy.

For simplicity, let $S_1(Z_1)=S_1$ and $\sigma _1(Z_1)=\sigma _1$. It follows from Lemma 1 that

$$\begin{aligned} \begin{aligned} z_1F_1=&z_1\theta _1^{\mathrm {T}}S_1+z_1\sigma _1\\ \le&\frac{g_1}{2a_1^2}z_1^2\varTheta _1^*S_1^{\mathrm {T}}S_1+\frac{1}{2}a_1^2+\frac{g_1}{2}z_1^2+\frac{1}{2g_1}(\sigma _1^*)^{2}, \end{aligned} \end{aligned}$$

(44)

with $\varTheta _1^*=\frac{\Vert \theta _1\Vert ^2}{g_1}$, and $a_1>0$.

$$\begin{aligned} g_1\varPi _1z_1\varrho _2\le \frac{g_1^2}{2}\varPi _1^2z_1^2+\frac{1}{2}\varrho _2^2. \end{aligned}$$

(45)

According to the design procedures of DSC, the following first-order low-pass filter will be employed to filter $\alpha _1$ and to obtain $H_2$

$$\begin{aligned} \beta _2{\dot{H}}_2+H_2=\alpha _1,~H_2(0)=\alpha _1(0), \end{aligned}$$

(46)

where $\beta _2>0$ is a time constant, $H_2$ is the output of the low-pass filter.

According to (46) and $\varrho _2=H_2-\alpha _1$, we have $\dot{H_2}=\frac{\alpha _1-H_2}{\beta _2}$. It is easy to learn ${\dot{H}}_2=-\frac{\varrho _2}{\beta _2}$. Therefore, we can obtain

$$\begin{aligned} \begin{aligned} {\dot{\varrho }}_2={\dot{H}}_2-{\dot{\alpha }}_1=&-\frac{\varrho _2}{\beta _2}-{\dot{\alpha }}_1, \\ |{\dot{\varrho }}_2+\frac{\varrho _2}{\beta _2}|\le&\varLambda _2 (z_1, z_2, \varrho _2, \varTheta _1, y_d, {\dot{y}}_d, \ddot{y}_d), \end{aligned} \end{aligned}$$

(47)

where $\varLambda _2$ is a nonnegative continuous function and its definition can be found in [17]. Meanwhile $\varLambda _2$ satisfies $\varLambda _2\le M_2$, and $M_2$ is the upper bound.

Based on Lemma 1, (47) can be written as

$$\begin{aligned} {\dot{\varrho }}_2\varrho _2\le -\frac{\varrho _2^2}{\beta _2}+|\varrho _2|\varLambda _2 \le -\frac{\varrho _2^2}{\beta _2}+\frac{1}{2}\varrho _2^2+\frac{1}{2}M_2^2. \end{aligned}$$

(48)

From (16), one has

$$\begin{aligned} \varPi _1g_1z_1\alpha _1=-\frac{g_1}{2a_1^2}z_1^2\varTheta _1S_1^{\mathrm {T}}S_1 -\frac{g_1}{2}z_1^2-g_1k_1z_1^2. \end{aligned}$$

(49)

Substituting (44)–(49) into (42), ${\dot{V}}_1$ is described as

$$\begin{aligned} \begin{aligned} {\dot{V}}_1\le&-(\lambda _0-\frac{1}{2})\Vert e\Vert ^2+\Vert P\Vert ^2\sum _{i=1}^{n}{\tilde{W}}_i^{\mathrm {T}}{\tilde{W}}_i+\varPhi _0\\&+\sum _{i=1}^{n-1}m_i{\hat{x}}_{i+1}^2 -z_1^2\sum _{l=1}^{n-1}q_{l1}(z_1) +g_1\varPi _1z_1z_2\\&-g_1k_1z_1^2-\frac{1}{\beta _2}\varrho _2^2+\varrho _2^2 +\frac{1}{2}a_1^2+\frac{1}{2g_1}(\sigma _1^*)^{2}\\&+\frac{1}{2}(d_1^*)^{2}+\frac{1}{2}M_2^2 +\frac{g_1\gamma _1}{\epsilon _1}{\tilde{\varTheta }}_1\varTheta _1 +\frac{\iota _1\kappa _1}{\eta _1}{\tilde{W}}_1^{\mathrm {T}}W_1. \end{aligned} \end{aligned}$$

(50)

Based on Lemma 1, we have

$$\begin{aligned} \frac{g_1\gamma _1}{\epsilon _1}{\tilde{\varTheta }}_1\varTheta _1\le & {} \frac{g_1\gamma _1}{2\epsilon _1} (\varTheta _1^*)^{2}-\frac{g_1\gamma _1}{2\epsilon _1}{\tilde{\varTheta }}_1^2, \end{aligned}$$

(51)

$$\begin{aligned} \frac{\iota _1\kappa _1}{\eta _1}{\tilde{W}}_1^{\mathrm {T}}W_1\le & {} \frac{\iota _1\kappa _1}{2\eta _1}({\tilde{W}}_1^*)^{\mathrm {T}}W_1^* +\frac{\iota _1\kappa _1}{2\eta _1}{\tilde{W}}_1^{\mathrm {T}}{\tilde{W}}_1. \end{aligned}$$

(52)

Substituting (51) and (52) into (50), yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_1\le&-\lambda _1\Vert e\Vert ^2+\varPhi _1+\sum _{i=1}^{n-1}m_i{\hat{x}}_{i+1}^2 -z_1^2\sum _{l=1}^{n-1}q_{l1}(z_1)\\&+\varPi _1g_1z_1z_2-g_1k_1z_1^2-\frac{1}{\beta _2}\varrho _2^2+\varrho _2^2 -\frac{g_1\gamma _1}{2\epsilon _1}{\tilde{\varTheta }}_1^2\\&-\frac{\iota _1\kappa _{1}}{2\eta _1}{\tilde{W}}_1^{\mathrm {T}}{\tilde{W}}_1+\Vert P\Vert ^2\sum _{i=1}^{n}{\tilde{W}}_i^{\mathrm {T}}{\tilde{W}}_i, \end{aligned} \end{aligned}$$

(53)

where

$$\begin{aligned} \begin{aligned} \lambda _1=&\lambda _0-\frac{1}{2},\\ \varPhi _1=&\varPhi _0+\frac{1}{2}a_1^2+\frac{1}{2g_1}(\sigma _1^*)^{2}+\frac{g_1\gamma _1}{2\epsilon _1}(\varTheta _1^*)^{2}\\&+\frac{\iota _1\kappa _1}{2\eta _1}(W_1^*)^{\mathrm {T}}W_1^*+\frac{1}{2}(d_1^*)^{2}+\frac{1}{2}M_2^2. \end{aligned} \end{aligned}$$

Step 2: From (8) and (14), one has

$$\begin{aligned} \begin{aligned} {\dot{z}}_2=&\dot{{\hat{x}}}_2-{\dot{H}}_2\\ =&g_{2,0}{\hat{x}}_3+l_2e_1+W_2^{\mathrm {T}}\varphi _2(\hat{{\bar{x}}}_2)-{\dot{H}}_2. \end{aligned} \end{aligned}$$

(54)

Consider the following Lyapunov function

$$\begin{aligned} V_2=\frac{1}{2}z_2^2+\frac{1}{2}\varrho _3^2+\frac{g_{2,0}}{2\epsilon _2}{\tilde{\varTheta }}_2^2 +\frac{\iota _2}{2\eta _2}{\tilde{W}}_2^{{\mathrm {T}}}{\tilde{W}}_2, \end{aligned}$$

(55)

where $\iota _2$, $\epsilon _2$ and $\eta _2$ are positive design parameters and ${\tilde{\varTheta }}_2=\varTheta _2^*-\varTheta _2$ is the approximation error, $\varTheta _2$ is the estimation of $\varTheta _2^*$, and ${\tilde{W}}_2=W_2^*-W_2$.

According to (53), (54), $z_3={\hat{x}}_3-H_3$ and $\varrho _3=H_3-\alpha _2$, the derivative of $V_2$ satisfies

$$\begin{aligned} \begin{aligned} {\dot{V}}_2=&z_2{\dot{z}}_2+\varrho _3{\dot{\varrho }}_3-\frac{g_{2,0}}{\epsilon _2}{\tilde{\varTheta }}_2{\dot{\varTheta }}_2 -\frac{\iota _2}{\eta _2}{\tilde{W}}_2^{{\mathrm {T}}}{\dot{W}}_2\\ =&z_2(g_{2,0}(z_3+\varrho _3+\alpha _2)+l_2e_1 +W_2^{{\mathrm {T}}}\varphi _2(\hat{{\bar{x}}}_2)-{\dot{H}}_2)\\&+\varrho _3{\dot{\varrho }}_3-\frac{g_{2,0}}{\epsilon _2}{\tilde{\varTheta }}_2{\dot{\varTheta }}_2 -\frac{\iota _2}{\eta _2}{\tilde{W}}_2^{{\mathrm {T}}}{\dot{W}}_2. \end{aligned} \end{aligned}$$

(56)

Based on $f_2(\hat{{\bar{x}}}_2)=(W_2^*)^{\mathrm {T}}\varphi _2(\hat{{\bar{x}}}_2)+\xi _2(\hat{{\bar{x}}}_2)$, we can obtain

$$\begin{aligned} \begin{aligned} {\dot{V}}_2=&z_2(F_2+g_{2,0}(z_3+\varrho _3+\alpha _2) -{\tilde{W}}_2^{\mathrm {T}}\varphi _2(\hat{{\bar{x}}}_2))+\varrho _3{\dot{\varrho }}_3-z_2^2\sum _{l=1}^{n-1}q_{l1}(z_2)\\&-\varPi _1g_1z_1z_2 -\frac{g_{2,0}}{\epsilon _2}{\tilde{\varTheta }}_2{\dot{\varTheta }}_2 -\frac{\iota _2}{\eta _2}{\tilde{W}}_2^{{\mathrm {T}}}{\dot{W}}_2, \end{aligned} \end{aligned}$$

(57)

where

$$\begin{aligned} \begin{aligned} F_2&(x_1, {\hat{x}}_1, {\hat{x}}_2, z_1, z_2, {\dot{H}}_2)=\varPi _1g_1z_1+l_2e_1-f_2(\hat{{\bar{x}}}_2)\\&+\xi _2(\hat{{\bar{x}}}_2)-{\dot{H}}_2+z_2\sum _{l=1}^{n-1}q_{l2}(z_2). \end{aligned} \end{aligned}$$

Applying the RBF-NNs $\theta _2^{\mathrm {T}}S_2(Z_2)$ to approximate the packaged function $F_2$, one has

$$\begin{aligned} F_2=\theta _2^{\mathrm {T}}S_2(Z_2)+\sigma _2(Z_2),~|\sigma _2|\le \sigma _2^* \end{aligned}$$

(58)

where $Z_2=(x_1, {\hat{x}}_1, {\hat{x}}_2, z_1, z_2, {\dot{H}}_2)$. $\sigma _2$ denotes the estimation error and $\sigma _2^*>0$ is an arbitrarily small estimation accuracy.

For simplicity, let $S_2(Z_2)=S_2$ and $\sigma _2(Z_2)=\sigma _2$. According to Lemma 1, the following inequality can be obtained

$$\begin{aligned} z_2F_2= & {} z_2\theta _2^{\mathrm {T}}S_2+z_2\sigma _2\nonumber \\\le & {} \frac{g_{2,0}}{2a_2^2}z_2^2\varTheta _2^*S_2^{\mathrm {T}}S_2+\frac{1}{2}a_2^2+\frac{g_{2,0}}{2}z_2^2+\frac{1}{2g_{2,0}}(\sigma _2^*)^{2}, \end{aligned}$$

(59)

$$\begin{aligned} g_{2,0}z_2\varrho _3\le & {} \frac{g_{2,0}^2}{2}z_2^2+\frac{1}{2}\varrho _3^2. \end{aligned}$$

(60)

where $\varTheta _2^*=\frac{\Vert \theta _2\Vert ^2}{g_{2,0}}$, and $a_2$ is a positive design parameter.

Let $\alpha _2$ pass through the following first-order filter to obtain $H_3$

$$\begin{aligned} \beta _3{\dot{H}}_3+H_3=\alpha _2,~H_3(0)=\alpha _2(0), \end{aligned}$$

(61)

where $\beta _3>0$ is a time constant, $H_3$ is the output of the low-pass filter.

According to (61), we have $\dot{H_3}=\frac{\alpha _2-H_3}{\beta _3}$. Defining $\varrho _3=H_3-\alpha _2$, it is easy to learn ${\dot{H}}_3=-\frac{\varrho _3}{\beta _3}$. Therefore, we can obtain

$$\begin{aligned} \begin{aligned} {\dot{\varrho }}_3={\dot{H}}_3-{\dot{\alpha }}_2=&-\frac{\varrho _3}{\beta _3}-{\dot{\alpha }}_2,\\ |{\dot{\varrho }}_3+\frac{\varrho _3}{\beta _3}|\le&\varLambda _3({\bar{z}}_3, \varrho _2, \varrho _3, \varTheta _1, \varTheta _2, y_d, {\dot{y}}_d, \ddot{y}_d), \end{aligned} \end{aligned}$$

(62)

where $\varLambda _3$ is a nonnegative continuous function and its definition can be found in [17]. Meanwhile $\varLambda _3$ satisfies $\varLambda _3\le M_3$, and $M_3$ is the upper bound.

According to Lemma 1, (62) can be written as

$$\begin{aligned} \begin{aligned} {\dot{\varrho }}_3\varrho _3\le&-\frac{\varrho _3^2}{\beta _3}+|\varrho _3|\varLambda _3\\ \le&-\frac{\varrho _3^2}{\beta _3}+\frac{1}{2}\varrho _3^2+\frac{1}{2}M_3^2. \end{aligned} \end{aligned}$$

(63)

According to (17), we can easy to obtain

$$\begin{aligned} g_{2,0}z_2\alpha _2=\frac{-g_{2,0}}{2a_2^2}z_2^2\varTheta _2S_2^{\mathrm {T}}S_2-g_{2,0}z_2^2 -g_{2,0}k_2z_2^2. \end{aligned}$$

(64)

By the utilization of (59)–(64), ${\dot{V}}_2$ can be given as

$$\begin{aligned} \begin{aligned} {\dot{V}}_2\le&-z_2^2\sum _{l=1}^{n-1}q_{l2}(z_2)+\frac{1}{2}a_2^2 -\frac{1}{\beta _3}\varrho _3^2+\frac{1}{2}\varrho _3^2\\&+\frac{1}{2g_{2,0}}(\sigma _2^*)^{2}-g_{2,0}k_2z_2^2+g_{2,0}z_2z_3-\varPi _1g_1z_1z_2\\&+\frac{1}{2}M_3^2+\frac{g_{2,0}\gamma _2}{\epsilon _2}{\tilde{\varTheta }}_2\varTheta _2 +\frac{\iota _2\kappa _2}{\eta _2}{\tilde{W}}_2^{{\mathrm {T}}}W_2. \end{aligned} \end{aligned}$$

(65)

Using Lemma 1, one has

$$\begin{aligned} \begin{aligned} \frac{g_{2,0}\gamma _2}{\epsilon _2}{\tilde{\varTheta }}_2^{\mathrm {T}}\varTheta _2 \le&\frac{g_{2,0}\gamma _2}{2\epsilon _2}(\varTheta _2^*)^{\mathrm {T}}\varTheta _2^* -\frac{g_{2,0}\gamma _2}{2\epsilon _2}{\tilde{\varTheta }}_2^{\mathrm {T}}{\tilde{\varTheta }}_2,\\ \frac{\iota _2\kappa _2}{\eta _2}{\tilde{W}}_2^{\mathrm {T}}W_2 \le&\frac{\iota _2\kappa _2}{W_2}(W_2^*)^{\mathrm {T}}W_2^* -\frac{\iota _2\kappa _2}{\eta _2}{\tilde{W}}_2^{\mathrm {T}}{\tilde{W}}_2. \end{aligned} \end{aligned}$$

(66)

According to (57), ${\dot{V}}_2$ can be expressed as

$$\begin{aligned} \begin{aligned} {\dot{V}}_2\le&-z_2^2\sum _{l=1}^{n-1}q_{l2}(z_2)-g_{2,0}k_2z_2^2+g_{2,0}z_2z_3-\varPi _1g_1z_1z_2 -\frac{1}{\beta _3}\varrho _3^2\\&+\varrho _3^2-\frac{g_{2,0}\gamma _2}{\epsilon _2}{\tilde{\varTheta }}_2^2 -\frac{\iota _2\kappa _2}{\eta _2}{\tilde{W}}_2^{{\mathrm {T}}}{\tilde{W}}_2+\varPhi _2, \end{aligned} \end{aligned}$$

(67)

where

$$\begin{aligned} \begin{aligned} \varPhi _2=&\frac{1}{2}a_2^2+\frac{1}{2g_{2,0}}(\sigma _2^*)^2 +\frac{g_{2,0}\gamma _2}{2\epsilon _2}(\varTheta _2^*)^{2} +\frac{\iota _2\gamma _2}{2\eta _2}(W_2^*)^{\mathrm {T}}W_2^* +\frac{1}{2}M_3^2. \end{aligned} \end{aligned}$$

Step i ($3\le i \le n - 1$): From (8) and (14), we can obtain

$$\begin{aligned} \begin{aligned} {\dot{z}}_i=&\dot{{\hat{x}}}_i-{\dot{H}}_i\\ =&g_{i,0}{\hat{x}}_{i+1}+l_ie_1+W_i^{\mathrm {T}}\varphi _i(\hat{{\bar{x}}}_i)-{\dot{H}}_i. \end{aligned} \end{aligned}$$

(68)

Consider the following Lyapunov function

$$\begin{aligned} V_i=\frac{1}{2}z_i^2+\frac{1}{2}\varrho _{i+1}^2+\frac{g_{i,0}}{2\epsilon _i}{\tilde{\varTheta }}_i^2 +\frac{\iota _i}{2\eta _i}{\tilde{W}}_i^{\mathrm {T}}{\tilde{W}}_i, \end{aligned}$$

(69)

where $\iota _i>0$, $\epsilon _i>0$ and $\eta _i>0$ are design parameters, ${\tilde{\varTheta }}_i=\varTheta _i^*-\varTheta _i$ is the estimation error, $\varTheta _i$ is the estimation of $\varTheta _i^*$, and ${\tilde{W}}_i=W_i^*-W_i$.

Similar to Step 2, ${\dot{V}}_i$ can be calculated as

$$\begin{aligned} \begin{aligned} {\dot{V}}_i=&z_i{\dot{z}}_i+\varrho _{i+1}{\dot{\varrho }}_{i+1} -\frac{g_{i,0}}{\epsilon _i}{\tilde{\varTheta }}_i^{\mathrm {T}}{\dot{\varTheta }}_i -\frac{\iota _i}{\eta _i}{\tilde{W}}_i^{\mathrm {T}}{\dot{W}}_i\\ =&z_i(g_{i,0}{\hat{x}}_{i+1}+l_ie_1+W_i^{\mathrm {T}}\varphi _i(\hat{{\bar{x}}}_i) -{\dot{H}}_i)+\varrho _{i+1}{\dot{\varrho }}_{i+1}\\&-\frac{g_{i,0}}{\epsilon _i}{\tilde{\varTheta }}_i^{\mathrm {T}}{\dot{\varTheta }}_i -\frac{\iota _i}{\eta _i}{\tilde{W}}_i^{\mathrm {T}}{\dot{W}}_i\\ =&z_i(g_{i,0}(z_{i+1}+\varrho _{i+1}+\alpha _i) +F_i-{\tilde{W}}_i^{\mathrm {T}}\varphi _i(\hat{{\bar{x}}}_i)) +\varrho _{i+1}{\dot{\varrho }}_{i+1}\\&-z_{i}^2\sum _{l=i-1}^{n-1}q_{l,i}(z_i) -g_{i-1,0}z_{i-1}z_i -\frac{\iota _i}{\eta _i}{\tilde{W}}_i^{\mathrm {T}}{\dot{W}}_i -\frac{g_{i,0}}{\epsilon _i}{\tilde{\varTheta }}_i^{\mathrm {T}}{\dot{\varTheta }}_i, \end{aligned} \end{aligned}$$

(70)

where

$$\begin{aligned} \begin{aligned} F_i(x_1, \hat{{\bar{x}}}_i,&z_{i-1}, z_i, {\dot{H}}_i)=g_{i-1,0}z_{i-1} +l_ie_1-f_i(\hat{{\bar{x}}}_i)\\&+\xi _i(\hat{{\bar{x}}}_i)+{\dot{H}}_{i}+z_i\sum _{l=i-1}^{n-1}q_{l,i}(z_i). \end{aligned} \end{aligned}$$

Applying the RBF-NNs $\theta _i^{\mathrm {T}}S_i(Z_i)$ to approximate the packaged function $F_i$, one has

$$\begin{aligned} F_i=\theta _i^{\mathrm {T}}S_i(Z_i)+\sigma _i(Z_i),~|\sigma _i|\le \sigma _i^*, \end{aligned}$$

(71)

where $Z_i=(x_1, \hat{{\bar{x}}}_i, z_{i-1}, z_i, {\dot{H}}_i)$. $\sigma _i$ denotes the estimation error and $\sigma _i^*>0$ is an arbitrarily small estimation accuracy.

For simplicity, let $S_i(Z_i)=S_i$ and $\sigma _i(Z_i)=\sigma _i$. Using Lemma 1, one has

$$\begin{aligned} z_iF_i= & {} z_i\theta _i^{\mathrm {T}}S_i+z_i\sigma _i\nonumber \\\le & {} \frac{g_{i,0}}{2a_i^2}\varTheta _i^*S_i^{\mathrm {T}}S_i+\frac{1}{2}a_i^2 +\frac{g_{i,0}}{2}z_i^2+\frac{1}{2g_{i,0}}(\sigma _i^*)^{2}, \end{aligned}$$

(72)

$$\begin{aligned} g_{i,0}z_i\varrho _{i+1}\le & {} \frac{g_{i,0}^2}{2}z_i^2+\frac{1}{2}\varrho _{i+1}^2, \end{aligned}$$

(73)

where $\varTheta _i^*=\frac{\Vert \theta _i\Vert }{g_{i,0}}$, and $a_i$ is the positive design parameter.

Let $\alpha _i$ pass through the following first-order filter to obtain $H_{i+1}$

$$\begin{aligned} \beta _{i+1}{\dot{H}}_{i+1}+H_{i+1}=\alpha _i,~H_{i+1}(0)=\alpha _i(0), \end{aligned}$$

(74)

where $\beta _{i+1}$ is a positive constant, $H_{i+1}$ is the output of the low-pass filter.

According to (74), we have ${\dot{H}}_{i+1}=\frac{\alpha _i-H_{i+1}}{\beta _i}$. Defining $\varrho _{i+1}=H_{i+1}-\alpha _i$, it is easy to learn ${\dot{H}}_{i+1}=-\frac{\varrho _{i+1}}{\beta _{i+1}}$. Therefore, we have

$$\begin{aligned} \begin{aligned} {\dot{\varrho }}_{i+1}={\dot{H}}_{i+1}-{\dot{\alpha }}_i=&-\frac{\varrho _{i+1}}{\beta _{i+1}}-{\dot{\alpha }}_i,\\ |{\dot{\varrho }}_{i+1}+\frac{\varrho _{i+1}}{\beta _{i+1}}|\le&\varLambda _{i+1}({\bar{z}}_{i+1}, \varrho _2,\ldots , \varrho _{i+1}, \\&\varTheta _1, \ldots , \varTheta _i,y_d, {\dot{y}}_d, \ddot{y}_d), \end{aligned} \end{aligned}$$

(75)

where $\varLambda _{i+1}$ is a nonnegative function and its definition can be found in [17]. Meanwhile $\varLambda _{i+1}$ satisfies $\varLambda _{i+1}\le M_{i+1}$, and $M_{i+1}$ is the upper bound.

According to Lemma 1, (75) can be written as

$$\begin{aligned} \begin{aligned} {\dot{\varrho }}_{i+1}\varrho _{i+1}\le&-\frac{\varrho _{i+1}^2}{\beta _{i+1}}+|\varrho _{i+1}|\varLambda _{i+1}\\ \le&-\frac{\varrho _{i+1}^2}{\beta _{i+1}}+\frac{1}{2}\varrho _{i+1}^2+\frac{1}{2}M_{i+1}^2. \end{aligned} \end{aligned}$$

(76)

From (18), one has

$$\begin{aligned} \begin{aligned} g_{i,0}z_i\alpha _{i}=-\frac{g_{i,0}}{2a_i^2}z_i^2\varTheta _iS_i^{\mathrm {T}}S_i -g_{i,0}z_i^2-g_{i,0}k_iz_i^2. \end{aligned} \end{aligned}$$

(77)

Substituting (72)–(77) into (70), ${\dot{V}}_i$ can be rewritten as

$$\begin{aligned} \begin{aligned} {\dot{V}}_i\le&-z_{i}^2\sum _{l=i-1}^{n-1}q_{l,i}(z_i)-g_{i,0}k_iz_i^2+g_{i,0}z_iz_{i+1} -g_{i-1,0}z_{i-1}z_i\\&+\frac{1}{2}a_i^2+\frac{1}{2g_{i,0}}(\sigma _i^*)^{2}+\frac{1}{2}M_{i+1}^2 -\frac{1}{\beta _i}\varrho _{i+1}^2+\varrho _{i+1}^2 \\&+\frac{g_{i,0}\gamma _i}{\epsilon _i}{\tilde{\varTheta }}_i^{\mathrm {T}}\varTheta _i +\frac{\iota _i\kappa _i}{\eta _i}{\tilde{W}}_i^{\mathrm {T}}W_i. \end{aligned} \end{aligned}$$

(78)

Using Lemma 1, we can obtain

$$\begin{aligned} \begin{aligned} \frac{g_{i,0}\gamma _i}{\epsilon _i}{\tilde{\varTheta }}_i^{\mathrm {T}}\varTheta _i\le&\frac{g_{i,0}\gamma _i}{2\epsilon _i}(\varTheta _i^*)^{\mathrm {T}}\varTheta _i^* -\frac{g_{i,0}\gamma _i}{2\epsilon _i}{\tilde{\varTheta }}_i^{\mathrm {T}}{\tilde{\varTheta }}_i,\\ \frac{\iota _i\kappa _i}{\eta _i}{\tilde{W}}_i^{\mathrm {T}}W_i\le&\frac{\iota _i\kappa _i}{2\eta _i}(W_i^*)^{\mathrm {T}}W_i^* -\frac{\iota _i\kappa _i}{2\eta _i}{\tilde{W}}_i^{\mathrm {T}}{\tilde{W}}_i. \end{aligned} \end{aligned}$$

(79)

And substituting (79) into (78), one has

$$\begin{aligned} \begin{aligned} {\dot{V}}_i\le&-z_i^2\sum _{k=i-1}^{n-1}q_{k,i}(z_i)-g_{i,0}k_iz_i^2+g_{i,0}z_iz_{i+1} -g_{i-1,0}z_{i-1}z_i\\&-\frac{1}{\beta _i}\varrho _{i+1}^2+\varrho _{i+1}^2 -\frac{g_{i,0}\gamma _i}{2\epsilon _i}{\tilde{\varTheta }}_i^2 -\frac{\iota _i\kappa _i}{2\eta _i}{\tilde{W}}_i^{\mathrm {T}}{\tilde{W}}_i+\varPhi _{i}, \end{aligned} \end{aligned}$$

(80)

where

$$\begin{aligned} \varPhi _i=\frac{1}{2}a_i^2+\frac{1}{2g_{i,0}}(\sigma _i^*)^{2} +\frac{g_{i,0}\gamma _i}{2\epsilon _i}(\varTheta _i^*)^{2} +\frac{\iota _i\kappa _i}{2\eta _i}(W_i^*)^{\mathrm {T}}W_i^*+\frac{1}{2}M_{i+1}^2. \end{aligned}$$

Step n: According to (8) and (14), one has

$$\begin{aligned} \begin{aligned} {\dot{z}}_n=&\dot{{\hat{x}}}_n-{\dot{H}}_n\\ =&c v(t)+h(v)+l_ne_1+W_n^{\mathrm {T}}\varphi _n(\hat{{\bar{x}}}_n)-{\dot{H}}_n. \end{aligned} \end{aligned}$$

(81)

Define the following Lyapunov function as

$$\begin{aligned} V_n=\frac{1}{2}z_n^2+\frac{1}{2\epsilon _n}{\tilde{\varTheta }}_n^2+ \frac{\iota _n}{2\eta _n}{\tilde{W}}_n^{\mathrm {T}}{\tilde{W}}_n, \end{aligned}$$

(82)

where $\iota _n>0$, $\epsilon _n>0$ and $\eta _n>0$.

Similar to Step i, we can obtain

$$\begin{aligned} \begin{aligned} {\dot{V}}_n=&z_n{\dot{z}}_n-\frac{1}{\epsilon _n}{\tilde{\varTheta }}_n{\dot{\varTheta }}_n -\frac{\iota _n}{\eta _n}{\tilde{W}}_n^{\mathrm {T}}{\dot{W}}_n\\ =&z_n(c v(t)+h(v)+l_ne_1+W_n^{\mathrm {T}}\varphi _n(\hat{{\bar{x}}}_n)-{\dot{H}}_{n})\\&-\frac{1}{\epsilon _n}{\tilde{\varTheta }}_n{\dot{\varTheta }}_n -\frac{\iota _n}{\eta _n}{\tilde{W}}_n^{\mathrm {T}}{\dot{W}}_n\\ =&z_n(F_n+c v(t)+h(v)-{\tilde{W}}_n^{\mathrm {T}}\varphi _n(\hat{{\bar{x}}}_n))\\&-g_{n-1,0}z_{n-1}z_{n}-\frac{1}{\epsilon _n}{\tilde{\varTheta }}_n{\dot{\varTheta }}_n -\frac{\iota _n}{\eta _n}{\tilde{W}}_n^{\mathrm {T}}{\dot{W}}_n, \end{aligned} \end{aligned}$$

(83)

where

$$\begin{aligned} \begin{aligned} F_n(x_1, \hat{{\bar{x}}}_n,&z_{n-1}, z_n, {\dot{H}}_n)=g_{n-1,0}z_{n-1}+l_ne_1\\&-f_n(\hat{{\bar{x}}}_n)+\xi _n(\hat{{\bar{x}}}_n)+{\dot{H}}_{n}+z_nq_{n-1,n}(z_n). \end{aligned} \end{aligned}$$

Applying the RBF-NNs $\theta _n^{\mathrm {T}}S_n(Z_n)$ to approximate the packaged function $F_n$, one has

$$\begin{aligned} F_n=\theta _n^{\mathrm {T}}S_n(Z_n)+\sigma _n(Z_n),~|\sigma _n|\le \sigma _n^* \end{aligned}$$

(84)

where $Z_n=(x_1, \hat{{\bar{x}}}_n, z_{n-1}, z_n, {\dot{H}}_n)$. $\sigma _n$ denotes the estimation error and $\sigma _n^*>0$ is an arbitrarily small estimation accuracy.

For simplicity, let $S_n(Z_n)=S_n$ and $\sigma _n(Z_n)=\sigma _n$. According to Lemma 1, we can obtain

$$\begin{aligned} \begin{aligned} z_nF_n=&z_n\theta _n^{\mathrm {T}}S_n+z_n\sigma _n\\ \le&\frac{1}{2a_n^2}z_n^2\varTheta _n^*S_n^{\mathrm {T}}S_n+\frac{1}{2}a_n^2+\frac{1}{2}z_n^2+\frac{1}{2}(\sigma _n^*)^{2}, \end{aligned} \end{aligned}$$

(85)

where $\varTheta _n^*=\Vert \theta _n\Vert ^2$, and $a_n$ is a positive constant.

Substituting (19) and (85) into (83), it yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_{n}\le&-(k_n-\frac{1}{2})z_n^2-g_{n-1,0}z_{n-1}z_n +\frac{1}{2}a_n^2+\frac{1}{2}(\sigma _n^*)^{2}\\&+\frac{\gamma _n}{\epsilon _n}{\tilde{\varTheta }}_n\varTheta _n +\frac{\iota _n}{\eta _n}{\tilde{W}}_n^{\mathrm {T}}W_n+z_nd(v). \end{aligned} \end{aligned}$$

(86)

Based on Lemma 1, one has

$$\begin{aligned} \frac{\gamma _n}{\epsilon _n}{\tilde{\varTheta }}_n^{\mathrm {T}}\varTheta _n\le & {} \frac{\gamma _n}{2\epsilon _n}(\varTheta _n^*)^{\mathrm {T}}\varTheta _n^* -\frac{\gamma _n}{2\epsilon _n}{\tilde{\varTheta }}_n^{\mathrm {T}}{\tilde{\varTheta }}_n, \end{aligned}$$

(87)

$$\begin{aligned} \frac{\iota _n}{\eta _n}{\tilde{W}}_n^{\mathrm {T}}W_n\le & {} \frac{\iota _n}{2\eta _n}(W_n^*)^{\mathrm {T}}W_n^* -\frac{\iota _n}{2\eta _n}{\tilde{W}}_n^{\mathrm {T}}{\tilde{W}}_n, \end{aligned}$$

(88)

$$\begin{aligned} z_nh(v)\le & {} \frac{1}{2}z_n^2+\frac{1}{2}({\bar{h}}^*)^{2}. \end{aligned}$$

(89)

Substituting (87)–(89) into (86), yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_{n}\le&-(k_n-\frac{1}{2})z_n^2-g_{n-1,0}z_{n-1}z_n -\frac{\gamma _n}{2\epsilon _n}{\tilde{\varTheta }}_n^2 -\frac{\iota _n\kappa _n}{2\eta _n}{\tilde{W}}_n^{\mathrm {T}}{\tilde{W}}_n+\varPhi _{n}, \end{aligned} \end{aligned}$$

(90)

where

$$\begin{aligned} \begin{aligned} \varPhi _{n}=&\frac{1}{2}(\sigma _{n}^*)^{2}+\frac{\gamma _{n}}{2\epsilon _n}(\varTheta _{n}^*)^{2} +\frac{1}{2}a_{n}^2+\frac{\iota _n\kappa _n}{2r_{2,n}}(W_{n}^*)^{\mathrm {T}}W_{n}^* +\frac{1}{2}({\bar{h}}^*)^{2}. \end{aligned} \end{aligned}$$