Skip to main content
SpringerLink
Log in

An Investigation Through Stochastic Procedures for Solving the Fractional Order Computer Virus Propagation Mathematical Model with Kill Signals

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

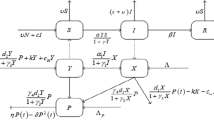
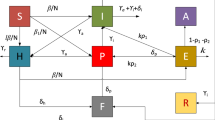
In this study, the numerical investigations through the stochastic procedures for solving a class of fractional order (FO) computer virus propagation (CVP) mathematical model with kill signals (KS), i.e., CVP-KS is presented. The KS gets alert about those viruses, which can be infected through the computer system to decrease the virus propagation danger. The mathematical model of the CVP-KS is based on the SEIR-KS model. The focus of these investigations is to present the numerical solutions of the FO-SEIR-KS model using the sense of Levenberg–Marquardt backpropagation scheme (LMBS) together with the neural networks (NNs), i.e., LMBS-NNs. The use of the one dynamic of the other makes the model nonlinear. Three different FO values have been used to check the performances of the designed scheme for this FO-SEIR-KS nonlinear mathematical model. The statics used in this study is 80%, 10% and 10% for training, testing and certification for solving the FO-SEIR-KS nonlinear mathematical model. The numerical simulations are performed through the stochastic LMBS-NNs scheme for solving the FO-SEIR-KS nonlinear mathematical model. The obtained results will be compared with the design of database reference solutions based on the Adams–Bashforth–Moulton. In order to accomplish the validity, capability, consistency, competence and accuracy of the LMBS-NNs, the numerical results using the error histograms, regression, mean square error, state transitions and correlation have been provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Han X, Tan Q (2010) Dynamical behavior of computer virus on Internet. Appl Math Comput 217:2520–2526

    MathSciNet  MATH  Google Scholar 

  2. Piqueira JRC, Araujo VO (2009) A modified epidemiological model for computer viruses. Appl Math Comput 213:355–360

    MathSciNet  MATH  Google Scholar 

  3. Kim J, Radhakrishana S, Jang J (2006) Cost optimization in SISmodel of worm infection. ETRI J 28:692–695

    Google Scholar 

  4. Yang LX, Yang X (2012) The spread of computer viruses under the influence of removable storage devices. Appl Math Comput 219:3914–3922

    MathSciNet  MATH  Google Scholar 

  5. Yang LX, Yang X, Wen L, Liu J (2012) A novel computer virus propagation model and its dynamics. Int J Comput Math 89:2307–2314

    MathSciNet  MATH  Google Scholar 

  6. Billings L, Spears WM, Schwartz IB (2002) A unified prediction of computer virus spread in connected networks. Phys Lett A 297:261–266

    MathSciNet  MATH  Google Scholar 

  7. Mishra BK, Pandey SK (2011) Dynamic model of worms with vertical transmission in computer network. Appl Math Comput 217:8438–8446

    MathSciNet  MATH  Google Scholar 

  8. Gan C, Yang X, Liu W, Zhu Q (2014) A propagation model of computer virus with nonlinear vaccination probability. Commun Nonlinear Sci Numer Simul 19:92–100

    MathSciNet  Google Scholar 

  9. Gan C, Yang X, Zhu Q, Jin J, He L (2013) The spread of computer virus under the effect of external computers. Nonlinear Dyn 73:1615–1620

    MathSciNet  MATH  Google Scholar 

  10. Muroya Y, Enatsu Y, Li H (2013) Global stability of a delayed SIRS computer virus propagation model. Int J Comput Math 91:347–367

    MathSciNet  MATH  Google Scholar 

  11. Feng L, Liao X, Li H, Han Q (2012) Hopf bifurcation analysis of a delayed viral infection model in computer networks. Math Comput Modell 56:167–179

    MathSciNet  MATH  Google Scholar 

  12. Zhu Q, Yang X, Yang LX, Zhang C (2012) Optimal control of computer virus under a delayed model. Appl Math Comput 218:11613–11619

    MathSciNet  MATH  Google Scholar 

  13. Ren J, Yang X, Yang L-X, Xu Y, Yang F (2012) A delayed computer virus propagation model and its dynamics. Chaos Solitons Fractals 45:74–79

    MathSciNet  MATH  Google Scholar 

  14. Zhu QY, Yang XF, Yang LX (2013) A mixing propagation model of computer viruses and countermeasures. Nonlinear Dyn 73:1433–1441

    MathSciNet  MATH  Google Scholar 

  15. Yang LX, Yang XF (2014) The pulse treatment of computer viruses: a modeling study. Nonlinear Dyn 76:1379–1393

    MathSciNet  MATH  Google Scholar 

  16. Yang LX, Draief M, Yang XF (2016) The optimal dynamics immunization under a controlled heterogeneous node-based SIRS model. Physica A 450:403–415

    MathSciNet  MATH  Google Scholar 

  17. Mishra BK, Jha N (2007) Fix period of temporary immunity after run of anti-malicious software on computer nodes. Appl Math Comput 190:1207–1212

    MATH  Google Scholar 

  18. Kephart JO, White SR (1993) Measure and modeling computer virus prevalence. In: IEEE computer society symposium research in security and privacy

  19. Changpin L, Yujiang W, Ruisong Y (2013) Recent advances in applied nonlinear dynamics with numerical analysis. World Scientific, Singapore

    MATH  Google Scholar 

  20. Baleanu D, Diethelm K, Scalas E, Trujill JJ (2012) Models and numerical methods. World Scientific, Singapore

    Google Scholar 

  21. Gorenflo R, Mainardi F (1997) Fractals and fractional calculus in continuum mechanics. Springer, New York, pp 223–276

    MATH  Google Scholar 

  22. Dabiri A, Moghaddam BP, Machado JAT (2018) Optimal variable-order fractional PID controllers for dynamical systems. J Comput Appl Math 339:40–48

    MathSciNet  MATH  Google Scholar 

  23. Evirgen F, Özdemir N (2012) A fractional order dynamical trajectory approach for optimization problem with HPM. In: Fractional dynamics and control. Springer, New York, NY, pp 145–155

  24. Koca I, Ozalp N (2013) Analysis of a fractional-order couple model with acceleration in feelings. Sci World J 2013:730736

  25. Li P, Chen L, Wu R, Machado JAT, Lopes AM, Yuan L (2018) Robust asymptotic stability of interval fractional-order nonlinear systems with time-delay. J Frankl Inst 355:7749–7763

    MathSciNet  MATH  Google Scholar 

  26. Rossikhin YA, Shitikova MV (1997) Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl Mech Rev 50(1):15–67

  27. Marks RJII, Hall M (1981) Differintegral interpolation from a bandlimited signal’s samples. IEEE Trans Acoust Speech Signal Process 29(4):872–877

    MATH  Google Scholar 

  28. Cole KS (1933) Electric conductance of biological systems. In: Cold Spring Harbor symposia on quantitative biology, vol 1. Cold Spring Harbor Laboratory Press, pp 107–116

  29. Jajarmi A, Baleanu D, Sajjadi SS, Asad JH (2019) A new feature of the fractional Euler–Lagrange equations for a coupled oscillator using a nonsingular operator approach. Front Phys 7:196

    Google Scholar 

  30. Kumar D, Singh J, Baleanu D (2020) On the analysis of vibration equation involving a fractional derivative with Mittag–Leffler law. Math Methods Appl Sci 43(1):443–457

    MathSciNet  MATH  Google Scholar 

  31. Singh J, Kumar D, Baleanu D, Rathore S (2019) On the local fractional wave equation in fractal strings. Math Methods Appl Sci 42(5):1588–1595

    MathSciNet  MATH  Google Scholar 

  32. Bhatter S, Mathur A, Kumar D, Singh J (2020) A new analysis of fractional Drinfeld–Sokolov–Wilson model with exponential memory. Physica A 537:122578

    MathSciNet  MATH  Google Scholar 

  33. Bhatter S, Mathur A, Kumar D, Nisar KS, Singh J (2020) Fractional modified Kawahara equation with Mittag–Leffler law. Chaos, Solitons Fractals 131:109508

    MathSciNet  MATH  Google Scholar 

  34. Boukhouima A, Hattaf K, Yousfi N (2017) Dynamics of a fractional order HIV infection model with specific functional response and cure rate. Int J Differ Equ 2017:8372140

  35. Singh J (2020) Analysis of fractional blood alcohol model with composite fractional derivative. Chaos, Solitons Fractals 140:110127

    MathSciNet  Google Scholar 

  36. Singh J, Kumar D, Baleanu D (2021) New aspects of fractional Bloch model associated with composite fractional derivative. Math Model Natl Phenomena 16:10–26

  37. Singh J, Kumar D, Hammouch Z, Atangana A (2018) A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl Math Comput 316:504–515

    MathSciNet  MATH  Google Scholar 

  38. Singh J, Gupta A, Baleanu D (2022) On the analysis of an analytical approach for fractional Caudrey–Dodd–Gibbon equations. Alex Eng J 61(7):5073–5082

    Google Scholar 

  39. Baleanu D, Jajarmi A, Mohammadi H, Rezapour S (2020) A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 134:109705

    MathSciNet  MATH  Google Scholar 

  40. Jajarmi A, Arshad S, Baleanu D (2019) A new fractional modelling and control strategy for the outbreak of dengue fever. Physica A 535:122524

    MathSciNet  MATH  Google Scholar 

  41. Ghanbari B et al (2020) Mathematical and numerical analysis of a three-species predator-prey model with herd behavior and time fractional-order derivative. Math Methods Appl Sci 43(4):1736–1752

    MathSciNet  MATH  Google Scholar 

  42. Ren J, Xu Y (2017) A compartmental model for computer virus propagation with kill signals. Physica A 486:446–454

    MathSciNet  MATH  Google Scholar 

  43. Özdemir N, Uçar S, Eroğlu BBİ (2020) Dynamical analysis of fractional order model for computer virus propagation with kill signals. Int J Nonlinear Sci Numer Simul 21(3–4):239–247

    MathSciNet  MATH  Google Scholar 

  44. Nisar K et al (2021) Design of morlet wavelet neural network for solving a class of singular pantograph nonlinear differential models. IEEE Access 9:77845–77862

    Google Scholar 

  45. Nisar K et al (2021) Evolutionary integrated heuristic with Gudermannian neural networks for second kind of Lane–Emden nonlinear singular models. Appl Sci 11:4725. https://doi.org/10.3390/app11114725

    Article  Google Scholar 

  46. Shoaib M et al (2021) Intelligent computing with Levenberg–Marquardt backpropagation neural networks for third-grade nanofluid over a stretched sheet with convective conditions. Arab J Sci Eng 43:1–19

  47. Sabir Z, Raja MAZ, Alnahdi AS, Jeelani MB, Abdelkawy MA (2022) Numerical investigations of the nonlinear smoke model using the Gudermannian neural networks. Math Biosci Eng 19(1):351–370

    MATH  Google Scholar 

  48. Naz S, Raja MAZ, Kausar A, Zameer A, Mehmood A, Shoaib M (2022) Dynamics of nonlinear cantilever piezoelectric–mechanical system: an intelligent computational approach. Math Comput Simul 196:88–113

  49. Kiani AK et al (2021) Intelligent backpropagation networks with bayesian regularization for mathematical models of environmental economic systems. Sustainability 13(17):9537

    Google Scholar 

  50. Anwar N et al (2022) Artificial intelligence knacks-based stochastic paradigm to study the dynamics of plant virus propagation model with impact of seasonality and delays. Eur Phys J Plus 137(1):1–47

    Google Scholar 

  51. Sabir Z, Umar M, Raja MAZ, Baskonus HM, Gao W (2021) Designing of Morlet wavelet as a neural network for a novel prevention category in the HIV system. Int J Biomath 15:2250012

  52. Sabir Z, Raja MAZ, Baleanu D, Cengiz K, Shoaib M (2021) Design of Gudermannian Neuroswarming to solve the singular Emden–Fowler nonlinear model numerically. Nonlinear Dyn 106:1–16

  53. Sabir Z, Raja MAZ, Guirao JL, Saeed T (2021) Meyer wavelet neural networks to solve a novel design of fractional order pantograph Lane–Emden differential model. Chaos Solitons Fractals 152:111404

    MathSciNet  MATH  Google Scholar 

  54. Sabir Z, Raja MAZ, Umar M, Shoaib M, Baleanu D (2021) FMNSICS: fractional meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane–Emden systems. Neural Comput Appl 34:1–14

  55. Naz S et al (2021) Weighted differential evolution heuristics for improved multilayer piezoelectric transducer design. Appl Soft Comput 113:107835

    Google Scholar 

  56. Ilhan E et al (2020) A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl Math Nonlinear Sci 5(1):171–188

    MathSciNet  MATH  Google Scholar 

  57. Sabir Z, Raja MAZ, Guirao JL, Saeed T (2021) Solution of novel multi-fractional multi-singular Lane–Emden model using the designed FMNEICS. Neural Comput Appl 33(24):17287–17302

    Google Scholar 

  58. Baskonus HM et al (2019) New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method. Appl Math Nonlinear Sci 4(1):141–150

    MathSciNet  MATH  Google Scholar 

  59. Sabir Z, Nisar K, Raja MAZ, Ibrahim AABA, Rodrigues JJ, Al-Basyouni KS, Mahmoud SR, Rawat DB (2021) Design of Morlet wavelet neural network for solving the higher order singular nonlinear differential equations. Alex Eng J 60(6):5935–5947

    Google Scholar 

  60. Sabir Z, Akhtar R, Zhiyu Z, Umar M, Imran A, Wahab HA, Shoaib M, Raja MAZ (2019) A computational analysis of two-phase casson nanofluid passing a stretching sheet using chemical reactions and gyrotactic microorganisms. Math Prob Eng 2019:1490571

  61. Sajid T et al (2021) Impact of oxytactic microorganisms and variable species diffusivity on blood-gold Reiner-Philippoff nanofluid. Appl Nanosci 11(1):321–333

    Google Scholar 

  62. Ayub A, Wahab HA, Sabir Z, Arbi A (2020) A note on heat transport with aspect of magnetic dipole and higher order chemical process for steady micropolar fluid. In: Computational overview of fluid structure interaction, p 97

  63. Ayub A et al (2021) Nanoscale heat and mass transport of magnetized 3-D chemically radiative hybrid nanofluid with orthogonal/inclined magnetic field along rotating sheet. Case Stud Therm Eng 26:101193

    Google Scholar 

Download references

Acknowledgements

The first author thanks the Faculty of Sciences and Liberal Arts, Rajamangala University of Technology Isan, Thailand.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan

    Zulqurnain Sabir

  2. Future Technology Research Center, National Yunlin University of Science and Technology, 123 University Road, Section 3, Douliou, 64002, Yunlin, Taiwan, ROC

    Muhammad Asif Zahoor Raja

  3. Department of Computer Science, Iqra University Islamabad Campus, Islamabad, Karachi, Pakistan

    Nadia Mumtaz

  4. Department of Islamic Educational Management, Institute Agama Islam Negeri Curup, Rejang Lebong, Indonesia

    Irwan Fathurrochman

  5. Department of Mathematics, Zagazig Faculty of Engineering, Zagazig University, Zagazig, Egypt

    R. Sadat

  6. Faculty of Engineering and Technology, Future University, Cairo, Egypt

    Mohamed R. Ali

Authors
  1. Zulqurnain Sabir
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Muhammad Asif Zahoor Raja
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nadia Mumtaz
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Irwan Fathurrochman
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. R. Sadat
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Mohamed R. Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. Sadat.

Ethics declarations

Conflict of interest

All authors describe that there are no potential conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sabir, Z., Raja, M.A.Z., Mumtaz, N. et al. An Investigation Through Stochastic Procedures for Solving the Fractional Order Computer Virus Propagation Mathematical Model with Kill Signals. Neural Process Lett 55, 1783–1797 (2023). https://doi.org/10.1007/s11063-022-10963-x

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-022-10963-x

Keywords

Search

Navigation