Skip to main content

Advertisement

Springer Nature Link
Log in

Convergence of Batch Gradient Method for Training of Pi-Sigma Neural Network with Regularizer and Adaptive Momentum Term

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

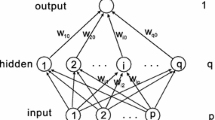
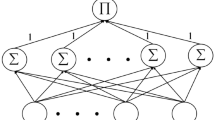
Pi-sigma neural network (PSNN) is a class of high order feed-forward neural networks with product units in the output layer, which leads to its fast convergence speed and a high degree of nonlinear mapping capability. Inspired by the sparse response character of human neuron system, this paper investigates the sparse-response feed-forward algorithm, i.e. the gradient descent based high order algorithm with self-adaptive momentum term and group lasso regularizer for training PSNN inference models. In this paper, we mainly focus on two challenging tasks. First, since the general group lasso regularizer is no differentiable at the original point, which will lead to the oscillation of the error function and the norm gradient during the training. A key point of this paper is to modify the usual group lasso regularization term by smoothing it at the origin. The advantage of this processing is that sparse and efficient neural networks can be obtained, and the theoretical analysis of the algorithm can also be obtained. Second, the adaptive momentum term is introduced in the iteration process to further accelerate the network learning speed. In addition, the numerical experiments show that the proposed algorithm eliminates the oscillation and increases learning rate in computation. And the convergence of the algorithm is also verified.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Haykin S (2008) Neural networks and learning machines. Prentice-Hall, Upper Saddle River

    Google Scholar 

  2. Ilias K, Michail P (2021) Predictive maintenance using machine learning and data mining: a pioneer method implemented to Greek railways. Designs 5(1):5

    Article  Google Scholar 

  3. Kocak C et al (2019) A new fuzzy time series method based on an ARMA-type recurrent Pi-Sigma artificial neural network. Soft Comput 24(11):8243–8252

    Article  Google Scholar 

  4. Bas E et al (2018) High order fuzzy time series method based on pi-sigma neural network. Eng Appl Artif Intell 72:350–356

    Article  Google Scholar 

  5. Liu T, Fan QW, Kang Q et al (2020) Extreme learning machine based on firefly adaptive flower pollination algorithm optimization. Processes 8(12):1583

    Article  Google Scholar 

  6. Wang J, Cai QL et al (2017) Convergence analyses on sparse feedforward neural networks via group lasso regularization. Inf Sci 381:250–269

    Article  MathSciNet  MATH  Google Scholar 

  7. Fan QW, Zhang ZW, Huang XD (2022) Parameter conjugate gradient with secant equation based Elman neural network and its convergence analysis. Adv Theory Simul. https://doi.org/10.1002/adts.202200047

    Article  Google Scholar 

  8. Shin Y, Ghosh J (1991) The pi-sigma network: an efficient higher-order neural network for pattern classification and function approximation. Int Jt Conf Neural Netw 1:13–18

    Google Scholar 

  9. Mohamed KS, Habtamu ZA et al (2016) Batch gradient method for training of pi-Sigma neural network with penalty. Int J Artif Intell Appl 7(1):11–20

    Google Scholar 

  10. Fan QW, Kang Q, Zurada JM (2022) Convergence analysis for sigma-pi-sigma neural network based on some relaxed conditions. Inf Sci 585:70–88

    Article  Google Scholar 

  11. Wu W, Feng G, Li X (2002) Training multilayer perceptrons via minimization of sum of ridge functions. Adv Comput Math 17(4):331–347

    Article  MathSciNet  MATH  Google Scholar 

  12. Zhang NM, Wu W, Zheng GF (2006) Convergence of gradient method with momentum for two-layer feedforward neural networks. IEEE Trans Neural Netw 17(2):522–5

    Article  Google Scholar 

  13. Augasta MG, Kathirvalavakumar T (2013) Pruning algorithms of neural networks—a comparative study. Open Comput Sci 3(3):105–115

    Article  Google Scholar 

  14. Fan QW, Liu T (2020) Smoothing \(L_0\) regularization for extreme learning machine. Math Probl Eng 2020:1–10

    MathSciNet  Google Scholar 

  15. Xu CY, Yang J et al (2018) SRNN: self-regularized neural network. Neurocomputing 273:260–270

    Article  Google Scholar 

  16. Setiono R, Hui LCK (1995) Use of a quasi-newton method in a feedforward neural network construction algorithm. Neural Netw IEEE Trans 6(1):273–277

    Article  Google Scholar 

  17. Zhang J, Morris AJ (1998) A sequential learning approach for single hidden layer neural networks. Neural Netw 11(1):65–80

    Article  Google Scholar 

  18. Augasta MG, Kathirvalavakumar T (2011) A novel pruning algorithm for optimizing feedforward neural network of classification problems. Neural Process Lett 34(3):241–258

    Article  Google Scholar 

  19. Hrebik R, Kukal J, Jablonsky J (2019) Optimal unions of hidden classes. Cent Eur J Oper Res 27(1):161–177

    Article  MathSciNet  MATH  Google Scholar 

  20. Sabo D, Yu XH (2008) Neural network dimension selection for dynamical system identification. IEEE International Conference on Control Applications. pp 972-977

  21. Setiono R (1997) A penalty-function approach for pruning feedforward neural networks. Neural Comput 9(1):185–204

    Article  MATH  Google Scholar 

  22. Wang J, Wu W, Zurada JM, (2011) Boundedness and convergence of MPN for cyclic and almost cyclic learning with penalty. Proceedings IEEE International Joint Conference on Neural Networks (IJCNN), pp 125–132

  23. Zhang H, Wu W, Liu F, Yao M (2009) Boundedness and convergence of online gradient method with penalty for feedforward neural networks. Neural Netw IEEE Trans 20(6):1050–1054

    Article  Google Scholar 

  24. Huynh TQ, Setiono R (2005) Effective neural network pruning using cross-validation. Proceedings IEEE international joint conference on neural networks(IJCNN). pp 972–977

  25. Hagiwara M (1994) A simple and effective method for removal of hidden units and weights. Neurocomputing 6(2):207–218

    Article  Google Scholar 

  26. Whitley D, Starkweather T, Bogart C (1990) Genetic algorithms and neural networks: optimizing connections and connectivity. Parallel Comput 14(3):347–361

    Article  Google Scholar 

  27. Fletcher L, Katkovnik V, Steffens FE, Engelbrecht AP (1998) Optimizing the number of hidden nodes of a feedforward artificial neural network. Proceedings IEEE world congress on computational intelligence. The international joint conference on neural networks, pp 1608–1612

  28. Belue LM, Bauer KW (1995) Determining input features for multilayer perceptrons. Neurocomputing 7(2):111–121

    Article  Google Scholar 

  29. Fan QW, Peng J, Li H, Lin S (2021) Convergence of a gradient-based learning algorithm with penalty for Ridge Polynomial Neural Networks. IEEE Access 9:28742–28752

    Article  Google Scholar 

  30. Zhang H, Wang J, Sun Z et al (2020) Feature selection for neural networks using group Lasso regularization. IEEE Trans Knowl Data Eng 32(1):659–673

    Article  Google Scholar 

  31. Loone SM, Irwin G (2001) Improving neural network training solutions using regularisation. Neurocomputing 37(1):71–90

    Article  MATH  Google Scholar 

  32. Xu ZB, Zhang H et al (2012) \(L_{1/2}\) regularization: a thresholding representation theory and a fast solver. IEEE Trans Netw Learn Syst 23(7):1013–1027

    Article  Google Scholar 

  33. Fan QW, Niu L, Kang Q (2020) Regression and multiclass classification using sparse extreme learning machine via smoothing group \(L_{1/2}\) regularizer. IEEE Access 8:191482–191494

    Article  Google Scholar 

  34. Mohamed KS, Wu W et al (2017) A modified higher-order feed forward neural network with smoothing regularization. Neural Netw World 27(6):577–592

    Article  Google Scholar 

  35. Zhou L, Fan QW, Huang XD, Liu Y (2022) Weak and strong convergence analysis of Elman neural networks via weight decay regularization. Optimization, pp 1-24. https://doi.org/10.1080/02331934.2022.2057852.

  36. Tibshirani R (1996) Regression shrinkage and selection via the lasso. J R Stat Soc Ser B (Methodological) 58(1):267–288

    MathSciNet  MATH  Google Scholar 

  37. Zou H (2006) The adaptive lasso and its oracle properties. J Am Stat Assoc 101(476):1418–1429

    Article  MathSciNet  MATH  Google Scholar 

  38. Yuan M, Lin Y (2006) Model selection and estimation in regression with grouped variables. J R Stat Soc 68(1):49–67

    Article  MathSciNet  MATH  Google Scholar 

  39. Friedman J, Hastie T, Tibshirani R (2010) A note on the group lasso and a sparse group lasso, Statistics

  40. Noah S, Friedman J, Hastie T, Tibshirani R (2013) A sparse group lasso. J Comput Graph Stat 22(2):231–245

    Article  MathSciNet  Google Scholar 

  41. Kang Q, Fan QW, Zurada JM (2021) Deterministic convergence analysis via smoothing group lasso regularization and adaptive momentum for sigma-pi-sigma neural network. Inf Sci 553:66–82

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Science, Xi’an Polytechnic University, Xi’an, 710048, China

    Qinwei Fan, Le Liu, Qian Kang & Li Zhou

Authors
  1. Qinwei Fan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Le Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Qian Kang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Li Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qinwei Fan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by the Natural Science Basic Research Plan in Shaanxi Province of China (No.2021JM-446) and the 65th China Postdoctoral Science Foundation (No.2019M652837), the Natural Science Foundation Guidance Project of Liaoning Province (No.2019-ZD-0128).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fan, Q., Liu, L., Kang, Q. et al. Convergence of Batch Gradient Method for Training of Pi-Sigma Neural Network with Regularizer and Adaptive Momentum Term. Neural Process Lett 55, 4871–4888 (2023). https://doi.org/10.1007/s11063-022-11069-0

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-022-11069-0

Keywords