Skip to main content
Springer Nature Link
Log in

Finite-Time Synchronization for T–S Fuzzy Complex-Valued Inertial Delayed Neural Networks Via Decomposition Approach

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

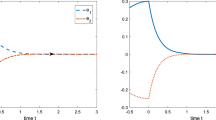
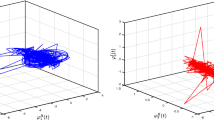
This paper is mainly dedicated to the issue of finite-time synchronization of T–S fuzzy complex-valued neural networks with time-varying delays and inertial terms via directly constructing Lyapunov functions with separating the original complex-valued neural networks into two real-valued subsystems equivalently. First of all, to facilitate the analysis of the second-order derivative caused by the inertial term, two intermediate variables are introduced to transfer complex-valued inertial delayed neural networks (CVIDNNs) into the first-order differential equation form. Next, CVIDNNs are developed using T–S fuzzy rules. By using the Lyapunov stability theory, inequality scaling skills and adjustable algebraic criteria for T–S fuzzy CVIDNNs as well as the upper bound of the settling time for synchronization, are derived. Finally, one numerical example with simulations is given to illustrate the effectiveness of our theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Rajivganthi C, Rihan A, Lakshmanan S, Rakkiyappan R, Muthukumar P (2016) Synchronization of memristor-based delayed BAM neural networks with fractional-order derivatives. Complexity 21:412–426

    MathSciNet  Google Scholar 

  2. Pratap A, Raja R, Cao J, Rihan FA, Seadawy AR (2020) Quasi-pinning synchronization and stabilization of fractional order BAM neural networks with delays and discontinuous neuron activations. Chaos, Solitons Fractals 131:109491

    MathSciNet  MATH  Google Scholar 

  3. Du Y, Zhong S, Zhou N (2014) Global asymptotic stability of Markovian jumping stochastic Cohen–Grossberg BAM neural networks with discrete and distributed time-varying delays. Appl Math Comput 243:624–636

    MathSciNet  MATH  Google Scholar 

  4. Xiao J, Wen S, Yang X, Zhong S (2020) New approach to global Mittag–Leffler synchronization problem of fractional-order quaternion-valued BAM neural networks based on a new inequality. Neural Netw 122:320–337

    MATH  Google Scholar 

  5. Lv X, Li X, Cao J, Perc M (2018) Dynamical and static multisynchronization of coupled multistable neural networks via impulsive control. IEEE Trans Neural Netw Learn Syst 29:6062–6072

    MathSciNet  Google Scholar 

  6. Zhuang J, Cao J, Tang L, Xia Y, Perc M (2020) Synchronization analysis for stochastic delayed multilayer network with additive couplings. IEEE Trans Syst, Man, Cybern: Syst 50:4807–4816

    Google Scholar 

  7. Zhang W, Wang X, You W, Chen J, Dai P, Zhang P (2019) RESLS: region and edge synergetic level set framework for image segmentation. IEEE Trans Image Process 29:57–71

    MathSciNet  MATH  Google Scholar 

  8. Ngo L, Cha J, Han JH (2019) Deep neural network regression for automated retinal layer segmentation in optical coherence tomography images. IEEE Trans Image Process 29:303–312

    MathSciNet  MATH  Google Scholar 

  9. Zhou Z, Zhang B, Yu X (2021) Infrared handprint classification using deep convolution neural network. Neural Process Lett 53:1065–1079

    Google Scholar 

  10. Xiao Y, Zijie Z (2020) Infrared image extraction algorithm based on adaptive growth immune field. Neural Process Lett 51:2575–2587

    Google Scholar 

  11. He K, Cao X, Shi Y, Nie D, Gao Y, Shen D (2019) Pelvic organ segmentation using distinctive curve guided fully convolutional networks. IEEE Trans Med Imaging 38:585–595

    Google Scholar 

  12. Yu X, Ye X, Zhang S (2022) Floating pollutant image target extraction algorithm based on immune extremum region. Digit Signal Process 123:103442

    Google Scholar 

  13. Long C, Zhang G, Hu J (2021) Fixed-time synchronization for delayed inertial complex-valued neural networks. Appl Math Comput 405:126272

    MathSciNet  MATH  Google Scholar 

  14. Long C, Zhang G, Zeng Z, Hu J (2022) Finite-time stabilization of complex-valued neural networks with proportional delays and inertial terms: a non-separation approach. Neural Netw 148:86–95

    Google Scholar 

  15. Huang C, Liu B (2019) New studies on dynamic analysis of inertial neural networks involving non-reduced order method. Neurocomputing 325:283–287

    Google Scholar 

  16. Wheeler DW, Schieve WC (1997) Stability and chaos in an inertial two-neuron system. Physica D 105:267–284

    MATH  Google Scholar 

  17. Alimi AM, Aouiti C, Assali EA (2019) Finite-time and fixed-time synchronization of a class of inertial neural networks with multi-proportional delays and its application to secure communication. Neurocomputing 332:29–43

    Google Scholar 

  18. Lakshmanan S, Prakash M, Lim CP, Rakkiyappan R, Balasubramaniam P, Nahavandi S (2018) Synchronization of an inertial neural network with time-varying delays and its application to secure communication. IEEE Trans Neural Netw Learn Syst 29:195–207

    MathSciNet  Google Scholar 

  19. Prakash M, Balasubramaniam P, Lakshmanan S (2016) Synchronization of Markovian jumping inertial neural networks and its applications in image encryption. Neural Netw 83:86–93

    Google Scholar 

  20. Muralisankar S, Gopalakrishnan N, Balasubramaniam P (2012) An LMI approach for global robust dissipativity analysis of T–S fuzzy neural networks with interval time-varying delays. Expert Syst Appl 39:3345–3355

    Google Scholar 

  21. Tan Y, Du D, Fei S (2018) Quantized filtering for T–S fuzzy networked systems with saturation non linearities: an output-dependent triggering method. ISA Trans 72:122–137

    Google Scholar 

  22. Liu Y, Lee S (2016) Stability and stabilization of Takagi–Sugeno fuzzy systems via sampled-data and state quantized controller. IEEE Trans Fuzzy Syst 24:635–644

    Google Scholar 

  23. Yue D, Tian E, Zhang Y, Peng C (2009) Delay-distribution-dependent stability and stabilization of T–S fuzzy systems with probabilistic interval delay. IEEE Trans Syst Man Cybern 39:503–516

    Google Scholar 

  24. Tan Y, Liu Y, Niu B, Fei S (2020) Event-triggered synchronization control for T–S fuzzy neural networked systems with time delay. J Franklin Inst 357:5934–5953

    MathSciNet  MATH  Google Scholar 

  25. Tong D, Zhu Q, Zhou W, Xu Y, Fang J (2013) Adaptive synchronization for stochastic T–S fuzzy neural networks with time-delay and Markovian jumping parameters. Neurocomputing 117:91–97

    Google Scholar 

  26. Duan L, Li J (2021) Fixed-time synchronization of fuzzy neutral-type BAM memristive inertial neural networks with proportional delays. Inf Sci 576:522–541

    MathSciNet  Google Scholar 

  27. Jian J, Duan L (2020) Finite-time synchronization for fuzzy neutral-type inertial neural networks with time-varying coefficients and proportional delays. Fuzzy Sets Syst 381:51–67

    MathSciNet  MATH  Google Scholar 

  28. Hao Z, Xing-yuan W, Peng-fei Y, Yu-jie Sun (2020) Combination synchronization and stability analysis of time-varying complex-valued neural networks. Chaos, Solitons Fractals 131:109485

  29. Zhang B, Deng F, Xie S, Luo S (2018) Exponential synchronization of stochastic time-delayed memristor-based neural networks via distributed impulsive control. Neurocomputing 286:41–50

    Google Scholar 

  30. Shi Y, Zhu P (2016) Finite-time synchronization of stochastic memristor-based delayed neural networks. Neural Comput Appl 29:293–301

    Google Scholar 

  31. Jiang M, Wang S, Mei J, Shen Y (2015) Finite-time synchronization control of a class of memristor-based recurrent neural networks. Neural Netw 63:133–140

    MATH  Google Scholar 

  32. Zhang ZQ, Cao JD (2018) Novel finite-time synchronization criteria for inertial neural networks with time delays via integral inequality method. IEEE Trans Neural Netw Learn Syst 30:1476–1485

    MathSciNet  Google Scholar 

  33. Hu LF, Zhong SM, Shi KB, Zhang XJ (2020) Further results on finite-time synchronization of delayed inertial memristive neural networks via a novel analysis method. Neural Netw 127:45–47

    Google Scholar 

  34. Long CQ, Zhang GD, Zeng ZG, Hu JH (2021) Finite-time lag synchronization of inertial neural networks with mixed infinite time-varying delays and state-dependent switching. Neurocomputing 433:50–58

    Google Scholar 

  35. Wu YB, Gao YX, Li WX (2020) Finite-time synchronization of switched neural networks with state-dependent switching via intermittent control. Neurocomputing 384:325–334

    Google Scholar 

  36. Bohner M, Rao VSH, Sanyal S (2011) Global stability of complex-valued neural networks on time scales. Differ Equ Dyn Syst 19:3–11

    MathSciNet  MATH  Google Scholar 

  37. Rajchakit G, Sriraman R (2021) Robust passivity and stability analysis of uncertain complex-valued impulsive neural networks with time-varying delays. Neural Process Lett 53:581–606

    Google Scholar 

  38. Chanthorn P, Rajchakit G, Ramalingam S, Lim CP, Ramachandran R (2020) Robust dissipativity analysis of hopfield-type complex-valued neural networks with time-varying delays and linear fractional uncertainties. Mathematics 8:595

    Google Scholar 

  39. Samidurai R, Sriraman R, Zhu S (2019) Leakage delay-dependent stability analysis for complex-valued neural networks with discrete and distributed time-varying delays. Neurocomputing 338:262–273

    Google Scholar 

  40. Chen X, Zhao Z, Song Q, Hu J (2017) Multistability of complex-valued neural networks with time-varying delays. Appl Math Comput 294:18–35

    MathSciNet  MATH  Google Scholar 

  41. Zhang Z, Liu X, Chen J, Guo G, Zhou S (2011) Further stability analysis for delayed complex-valued recurrent neural networks. Neurocomputing 251:81–89

    Google Scholar 

  42. Liang J, Gong W, Huang H (2016) Multistability of complex-valued neural networks with discontinuous activation functions. Neural Netw 84:125–142

    MATH  Google Scholar 

  43. Yu J, Hu C, Jiang H, Wang L (2020) Exponential and adaptive synchronization of inertial complex-valued neural networks: a non-reduced order and non-separation approach. Neural Netw 124:50–59

    MATH  Google Scholar 

  44. Li X, Fang J, Huang T (2020) Event-triggered exponential stabilization for state-based switched inertial complex-valued neural networks with multiple delays. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2020.3031379

  45. Amin MdF, Murase K (2009) Single-layered complex-valued neural network for real-valued classification problems. Neurocomputing 72:945–955

    Google Scholar 

  46. Velmurugan G, Rakkiyappan R, Lakshmanan S (2015) Passivity analysis of memristor-based complex-valued neural networks with time-varying delays. Neural Process Lett 42:517–540

    Google Scholar 

Download references

Acknowledgements

This work was supported by the National Board Higher Mathematics, Mumbai, India, under the Sanctioned No. 02011/10/2019/NBHM(R.P)/R D II / 1242 and the National Natural Science Foundation of China under Grant No. 62103103, and the Natural Science Foundation of Jiangsu Province of China under Grant No. BK20210223.

Author information

Authors and Affiliations

  1. Department of Mathematics, Thiruvalluvar University, Vellore, 632 115, India

    S. Ramajayam & R. Samidurai

  2. Department of Mathematics, Adhiparasakthi College of Arts and Science (Autonomous), Ranipet, 632 506, India

    S. Rajavel

  3. School of Cyber Science and Engineering, Southeast University, Nanjing, 211189, China

    Yang Cao

Authors
  1. S. Ramajayam
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. Rajavel
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. R. Samidurai
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yang Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yang Cao.

Ethics declarations

Conflict of interest

The authors have no conflicts of interest to declare. All co-authors have seen and agree with the contents of the manuscript and there is no financial interest to report.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ramajayam, S., Rajavel, S., Samidurai, R. et al. Finite-Time Synchronization for T–S Fuzzy Complex-Valued Inertial Delayed Neural Networks Via Decomposition Approach. Neural Process Lett 55, 5885–5903 (2023). https://doi.org/10.1007/s11063-022-11117-9

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-022-11117-9

Keywords