Abstract
The capability to disentangle underlying factors hidden in the observable data, thereby obtaining their abstract representations, is considered one important ingredient for the subsequent success of deep networks in various application scenarios. Recently, numerous practical measures and learning strategies have been established for disentanglement, showcasing their potential in improving the model’s explainability, controlability, and robustness. However, when the downstream tasks come to the classification issues, there is still no consensus in the community on the definition or measurement for disentanglement, and its connection to the generalization capacity remains not very clear. Aiming at this, we explore the highly non-linear effect of a specified hidden layer on the generalization capacity from an information perspective and obtain a tight bound. Upon decompsing the bound, we find that besides the unsupervised disentanglement measure term in the conventional sense, a new supervised disentanglement term also emerges with a nonnegligible effect on the generality. Consequently, a novel label-based disentanglement measure (LDM) is naturally introduced as the discrepancy between these two terms under the supervised learning settings to substitute the commonly used unsupervised disentanglement measure. The theoretical analysis reveals an inverse relationship between the defined LDM and the generalization capacity. Finally, using LDM as regularizer, the experiments show that the deep neural networks (DNNs) can effectively reduce generalization error while improving classification accuracy when noise is added to the data features or labels, which strongly supports our points.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Disentangling underlying factors into distinct variables to obtain the abstract representations of observable data, known as disentangled representation learning, is a fundamental and widely used learning strategy [1]. Recently, advancements in statistical information, causal theory, and symmetry theory have inspired researchers. They have proposed numerous disentanglement measurements and learning paradigms for practical learning architectures, such as variational autoencoders (VAEs) and generative adversarial networks (GANs), etc. [2,3,4,5,6,7,8,9]. These developments have found extensive applications in various domains, such as image processing [2, 10] and natural language processing [11, 12], where disentanglement has proven its efficacy in enhancing model explainability, controllability, and robustness.
However, when the downstream task solely focuses on classification, although some studies have explored the statistical correlations between hidden units of DNNs and reported supporting experimental results in improving generality [13, 14], there is still a lack of consensus on the definition of disentanglement measurement, and the impact of disentanglement on generality remains not very clear and requires further theoretical investigation. Actually, some researchers, such as Locatello et al. [15], hold doubts about the usefulness of disentanglement when there are no inductive biases in both the learning approaches and the dataset, and demonstrated adverse experimental results precisely. It has also been suggested that merely considering disentanglement over the whole mixed data distribution but neglecting the subsistent local clustering feature of different classes may be harmful to the classification task [16].
In this study, we present a novel theoretical framework introducing the definition of our label-based disentanglement measure (LDM) and elucidating its relationship with generalization performance. Concretely, for a given hidden layer to be analyzed, by treating each hidden unit as a base mapping, we first derive a generalization error bound that captures the highly non-linear effect of the hidden layer on generality from an information theoretical perspective [17]. Compared to the traditional generalization error bounds based on the hypothesis space (e.g., Rademacher complexity [18]) or certain algorithm properties (e.g., uniform stability [19]), the derived bound incorporates all the ingredients of a learning problem, such as the input dataset, hypothesis space, and learning algorithm, which make the bound potentially more tightly coupled to the generalization error and the analysis on the bound more instructive and credible.
Subsequently, by decomposing the bound, we reveal that apart from the unsupervised disentanglement term in the conventional sense, a supervised disentanglement term, acting as an inductive bias in classificaiton, may also has an important impact on the generality. Taking both the two terms into account, we define LDM as the discrepancy between them. Further, based on the decomposition, an inverse relationship between LDM and the generalization capacity can be deduced directly. It’s worth noting that LDM extends the concept of redundancy introduced by Brown and Zhou et al. [20, 21] in the context of ensemble learning to the situations that are not constrained by the limitations of the 0-1 loss function and the Bayesian learning framework. Furthermore, some results in Achille’s work [22], such as the relationship between total correlation, the regularizer in the Bottleneck Lagrangian [23], and the information contained in the weights about the input dataset, can be readily derived from our decomposition results.
Finally, we introduce a novel regularization approach termed the LDM-method by using LDM as the regularizer. We conduct a series of experiments using practical architectures and real-world datasets to verify the assumptions underlying our assertions. Specifically, we demonstrate that the value of LDM can be efficiently reduced by the regularization method. Notably, this reduction, in turn, leads to a pronounced and theoretically predicted improvement in generality and classification accuracy when noise was added to the features or labels.
2 Preliminaries
Let \(\mathcal {Z} = (\mathcal {X}, \mathcal {Y})\) be an instance space, where \(\mathcal {X}\) is a feature space and \(\mathcal {Y}\) is a label space. A training set S of size n is an n-tuple, i.e.,
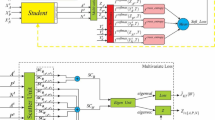
of i.i.d random elements from \(Z=(X, Y)\in \mathcal {Z}\) with an unknown PDF \(P_Z(z)\). Given a neural network with multiple layers, let \(\hat{h}= (h_1, h_2,...,h_m)\) be the set of all hidden units \(h_i\) in the discussed layer, and let \(W\in \mathcal {W}\) be the collection of model parameters from the specified hidden layer to the end layer, where \(\mathcal {W}\) is the hypothesis space of W (see Fig. 1). Due to the randomness in the realization of the dataset S, the values in W are considered to be random variables.
We will frequently use the following standard information-theoretical quantities [24]. For a stochastic variable X, its Shannon entropy is defined as
where \(\mathbb {E}_{X}[\cdot ]\) denotes the expectation of the random object within the brackets w.r.t to the subscript random variable X.
The mutual information of two stochastic variables is
which by capturing the nonlinear statistical dependencies between the variables can be reformulated as the Kullback–Leibler (KL-) divergence between the joint density and the product of the marginal densities, i.e.,
which is zero if and only if \(h_1\) and \(h_2\) are independent. For more than two variables, the multivariate mutual information is defined as
which is an extension of mutual information. We will later use it to measure the conventional part of disentanglement in the hidden units and still call it mutual information for consistency. Consequently, the conditional mutual information of multiple variables given Y is
which will be employed below to describe the class-conditional correlation.
3 Generalization Error
This section derives an upper-bound for the generalization error from an information theoretical perspective. Although, as analyzed in the introduction, it is important to ensure that the learned factors are disjoint in representation learning, there are various factors of different granularity to consider. Intuitively, for classification problems, the learned factors should contribute to subsequent classification tasks. This implies that the representations of samples from different classes should exhibit variability, indicating they are label-conditionally correlated. Enhancing such correlations is expected to amplify differences in representations among samples from different classes, thereby improving classification performance. Further, for better theoretical analysis, particularly in the context of deep learning, it is crucial to establish a clear connection between the well-defined concept of disentanglement of the hidden units in a specified layer and their generalization capacity under supervised settings. However, to ensure that the subsequent analysis is more inductive, the proposed upper-bound for generalization error must be closely tied to the specific characteristics of the current learning problem, including its input dataset, learning algorithm, and hypothesis space. This specificity limits the applicability of traditional error bounds in this work, such as VC dimension or Rademacher complexity, which mainly depend on the hypothesis space and neglect the learning algorithm, potentially leading to a looser quantity of bound to unify the ignored elements in the learning problem.
Based on these considerations, we follow the work of Russo and Xu et al. [17, 25], which can meet the above requirements. In this case, it is convenient to treat each unit in the discussed layer as a mapping from the datum to its activation value, i.e., \(h_i: \mathcal {X} \rightarrow \mathbb {R} (i=1,...,m)\), to investigate the effect of disentanglement of the hidden units on the generalization capacity since generalization capacity is initially related to the datum rather than to the values of the hidden units; and we are actually more interested in the mechanism that produces the activation value than in the activation value itself (see Fig. 1). Consequently, let \(\hat{h}(X) = (h_1(X),..., h_m(X))\), \(f(Z) = (\hat{h}(X), Y)\); then, given \(W\in \mathcal {W}\), the loss function l on the sample Z can be restated as a function w.r.t. f(Z) and W, i.e., \(l:\mathcal {W}\times f(\mathcal {Z})\rightarrow \mathbb {R}^{+}\), where \(Z=(X, Y)\). Accordingly, let \(f(S) = \left( f(Z^1),..., f(Z^n)\right) \). Now, we are ready to obtain the upper bound.
The generalization error is formulated as the absolute difference in the expectation between the expected risk and the empirical risk. The empirical risk of a hypothesis \(W\in \mathcal {W}\) over the dataset S is
The expected risk of W on \(P_{S}\) is
where \(F^k=f(Z^k)\) \((1 \le k \le n)\) are i.i.d random variables. Taking the expectation on the difference of \(L_{f(S)}(W)\) and \(L_{\overline{f(S)}}(W)\) with respect to the joint distribution \(P_{(S,W)}(s, w)\), we obtain the expected generalization error as
Then, the expected risk can be decomposed as
We focus on \(g(P_S,P_{W|S})\), which reflects the quality of the generalization of the output hypothesis. Substituting Eqs. (7) and (8) into Eq. (9) shows that
where \(\mathbb {E}_{f(S)\otimes W}\) means taking the expectation w.r.t the product of the marginal PDFs of f(S) and W.
Xu and Raginsky (Lemma 1 in [17]) have justified that given two random variables X and Y with the joint PDF \(P_{XY}\) and the product of the marginal PDFs \(P_{\overline{X}\overline{Y}}=P_X\otimes P_Y\), if the function C(X, Y) is a \(\sigma -\)subgaussian function under \(P_{\overline{X}\overline{Y}}\), then
Here, a random variable U is \(\sigma \)-subgaussian if \(\log \mathbb {E}\left[ e^{\gamma (U-\mathbb {E}[U])}\right] \le \gamma ^2\sigma ^2/2\) for all \(\gamma \in \mathbb {R}\). In fact, if the loss function in Eqs. (7) and (8) is restricted to be a bounded function within the interval [a, b], such as the commonly used logistic loss, hinge loss and cross-entropy loss (when used in combination with the softmax function), it becomes a \(\sigma \)-subgaussian function as per Hoeffding’s lemma [26]. Consequently, \(L_{f(S)}(W)\) in Eq. (11) can be considered a \(\sigma /\sqrt{n}\)-subgaussian function for W due to the independence among \(f(Z^k)\) \((1\le k \le n)\), where \(\sigma = (b-a)/2\).
Then, following Eq. (12), by setting \(L_{f(S)}(W)\), X, and Y in Eq. (12) as C, f(S), and W, respectively, we can derive the following lemma.
Lemma 1
If the loss function l is bounded in [a, b] and is thus \(\sigma \)-subgaussian, then the absolute value of \(g(P_S, P_{W|S})\) is upper-bounded in terms of the mutual information between f(S) and W, i.e.,
It is worth noting that the mutual information between the input dataset and the weights in the model, i.e., I(S, W), has been empirically used to describe the model’s complexity, demonstrating the presence of the bias-variance trade-off effect in experiments [22], which can generally not be replicated when using the number of parameters as a measure of model complexity [27].
4 Label-Based Disentanglement Measure
Lemma 1 implies that regularizing the empirical risk with I(f(S); W) may lead to improved generalization capacity. However, due to the high dimensions of the hypothesis space \(\mathcal {W}\), the direct usage of I(f(S); W) is usually intractable. In this section, we decompose the upper bound in Eq. (13), remove the terms related to W, and naturally derive a label-based disentanglement measure among the hidden units.
Theorem 1
Decomposing the non-constant part of the upper bound in Eq. (13), we obtain
where \(S_x = \{X_1,...,X_n\}\), \(S_y = \{Y_1,...,Y_n\}\) and \(\hat{h}(S_x) = \{{h}(X_1),...,{h}(X_n)\}\).
Proof
By the defition of mutual information, i.e., Eq. (3), we can express I(f(S); W) as follows
Furthermore, using Eq. (3) again, we find
Adding the left-hand side of the above equation to the right-hand side of the previous equation, we obtain:
where the components from Eq. (16) are denoted by underlines. Next, we break down the right-hand side of the above equation for separate computation.
For the second line in Eq. (17), we obtain
Furthermore, for the third line, we have
Combining Eqs. (17), (18) and (19), we otain
Note \(I\big (h_1(S_x);...;h_m(S_x)|S_y\big )\) in the above equation can be simplified:
where the fact that the samples \((X_i, Y_i) (1 \le i \le n)\) in S are sampled in an i.i.d. fashion is used in the derivation.
Similarly, we have
and
Combining Eqs. (20), (21), (22), (23), we obtain Eq. (14). \(\square \)
Let us focus on Eq. (14). There are five terms. Only the first two terms are completely unrelated to the sample size n and the model parameters W, reflecting the relationships among the hidden units. We argue that the two terms naturally quantify the disentanglement among the hidden units (see Definition 1). Since the two terms are part of the decomposed upper bound, regularizing the empirical risk with their sum is expected to reduce the upper bound of the absolute value of \(g(P_S, P_{W|S})\) as well as the generalization error.
The remaining terms are not considered as part of the disentanglement measure: the third term, which is the sum of the respective relevancy of the hidden units \(h_i (1\le i \le m)\) to the labels Y, demonstrates the classification ability of each hidden unit itself; the fourth term H(Y) is the intrinsic randomness of the labels in the dataset, which is non-optimizable w.r.t. the training process; compared to the other terms, the last term is the only one related to the sample size n and the model parameters W, reflecting the influence of W on the generality. Nonetheless, when the sample size is relatively large, this term tends to be relatively small and consequently has a small effect on the generalization error. Furthermore, it is worth noting that Achille et al. have also derived a similar term \(I(Y, W|\hat{h}(X))\) to the last term from the perspective of cross-entropy loss and demonstrated that reducing the term can enhance the model’s generalization, which aligns with the conclusions of this paper due to the established relationship between entropy and mutual information [22].
Definition 1
The label-based disentanglement measure among the hidden units is defined as
The first term in the disentanglement definition, known as the total correlation, is independent of the label, which is similar to most disentanglement measure concepts proposed in the present literature for improving generality or for learning better feature representation [5, 6]. It has also theoretically been proven to be bounded by I(S, W) by Achille et al. [22]. The second term in the definition is a label-based supervised term. It reflects the local clustering feature captured by the hidden units. Improving this term may potentially strengthen the class-conditional correlation and make the activations of the same class behave more collaboratively, which is usually important for a classification task. However, there is currently very little discussion on it.
Setting the discrepancy between the two terms as the disentanglement measure can be interpreted as a response to the discourse presented by Locatello et al. [15], suggesting that in scenarios where there are no inductive biases present in both the learning approaches and the dataset, disentanglement might not significantly benefit downstream classification tasks. Actually, reducing only the first unsupervised term without considering the labels Y, the value of the disentanglement measure would not decrease since the second term can potentially equal the first in this case, and then it has no effect on the generalization capacity.
It is worth mentioning that our disentanglement measure has a similar form to the diversity measure proposed by Brown and Zhou et al. in [20, 21]. They focused on ensemble learning and derived their ensemble diversity definition in the Bayesian learning framework from the upper bound of the probability of classification error, where only 0-1 loss is permitted. Nonetheless, according to their work, if we treat each unit in the hidden layer as a base learner, we can directly obtain the following bound for the probability of error of the combination function \(C(\cdot )\):
which implies that the improvement of our label-based disentanglement measure may well lead to a decrease in the ensemble classification error.
5 Regularization Method
In this section, a new LDM based regularization method (abbreviated as LDM-method for simplicity) is proposed. Its total loss function is formulated as
where \(E_{loss}\) is the premier loss function of the DNNs without any regularization, such as the mean squared error (MSE) between the outputs of DNNs and the input samples; \(D_{L}\) controls the label-based diversity among the hidden units in a specified layer; and \(\lambda > 0\) is the balancing parameter.
The regularizer \(D_{L}\) is, in fact, the difference between two mutual information terms. While the estimation of mutual information has been considered a challenging problem due to the continuity and high dimensions of data, recent studies [5, 28] have shown that this problem can be addressed using the Donsker-Varadhan representation [29] of KL-based mutual information, which can be expressed as:
where T is typically implemented as a neural network, ensuring that both expectations are finite. Subsequently, using Equation (5), mutual information is estimated by optimizing T to minimize the divergence between the joint distribution and the product of the marginals. However, this strategy for KL-based mutual information may suffer from instability. As our primary interest lies in optimizing mutual information rather than being concerned with its precise value, an alternative approach is to employ Jensen-Shannon (JS-) divergence-based mutual information, which has been found [5, 6] to be more stable and to provide better results compared to KL-divergence-based mutual information. That is,
where \(D_{JS}\) is JS-divergence. It can be estimated as follows:
where \(\overline{h} = (\overline{h_1}, \overline{h_2},...,\overline{h_m})\) obeys the distribution \(\otimes _{i=1}^{m}P_{h_i}\) and hereinafter \(\sigma (\cdot )\) represents the sigmoid function. In practical implementation, the instantiation sample of \(\overline{h}\) can be constructed by combining randomly selected \(h_i\) from different samples of \(\hat{h}\). For example, given (\(h^{(1)}_1\), \(h^{(1)}_2\)) and (\(h^{(2)}_1\), \(h^{(2)}_2\)) for sample 1 and 2, then \(\bar{h}\) could be (\(h^{(1)}_1\), \(h^{(2)}_2\)) or (\(h^{(2)}_1\), \(h^{(1)}_2\)), etc.
Similarly, for the conditional mutual information, we have
where taking expectation on Y requires using Eq. (29) to first obtain the corresponding JS-divergence for any given Y and combining the obtained divergence according to the prior probability of Y, which is estimated by the proportion of samples of each class to the total. To distinguish the network T used in Eqs. (28) and (30), they are denoted by \(T_1\) and \(T_2\), respectively. For brevity, the JS-divergence for conditional mutual information is abbreviated as \(D_{JS}^L\).
The learning algorithm is finally shown as an iterative min-max process:
where the maximization process ensures a sufficient approximation to the true LDM by \(T_1\) and \(T_2\), while the minimization process corresponds to the training process of the regularizing DNNs to obtain the model \(\theta \). The overall training process of LDM-method is analogous to that of Generative Adversarial Networks (GANs) [30]. In fact, both \(T_1\) and \(T_2\) in the LDM-method serve the same purpose as the discriminator in GANs (refer to Fig. 2).
To implement the learning algorithm presented in Eq. (31), it is crucial to first estimate the expectations. The expectation taken from the joint distribution \(P_{\hat{h}}\) or \(P_{\hat{h}|Y}\) can be directly estimated by calculating its average value from the samples derived from the joint distribution. However, obtaining the expectation from the product of marginals \(P_{\overline{h}}\) or \(P_{\overline{h}|Y}\) is not straightforward because there are no available samples from such a distribution for empirical estimation. In this work, two strategies are established to approximately obtain samples from the product of marginals depending on the type of network. For the case of fully connected neural networks, each sample from the product of marginals with M dimensions is obtained by randomly selecting M samples from the joint distribution, taking the ith element from the ith selected sample and then combining them. For convolutional neural networks (CNNs), we treat each filter in the specified layer as a map, considering each group of mapped values of all the filters from the same piece of images as a sample from the joint distribution. For instance, in cases where there are three filters in the specified CNNs layer, the samples from the joint distribution are regarded as vectors with three mapped values from all three filters. Using the same method applied to fully connected neural networks, we can obtain samples from the product of marginals, thus determining the LDM value for CNNs. The implementation of the LDM-method is presented in Algorithm 1 (also refer to Fig. 2).
6 Experiments
We aim to determine whether the regularizer can reduce the LDM value within the data and whether this reduction can lead to a better representation for classification and improvements in classification accuracy and generalization capacity.
6.1 Dataset
The experiments were conducted on three datasets: the MNIST dataset [31], the CIFAR-10 dataset [32] and Mini-ImageNet dataset [33]. MNIST comprises a training set of 60,000 images and a test set of 10,000 images, with each image having a size of 28x28 pixels. The CIFAR-10 dataset consists of 60,000 images with a size of 32x32 pixels, which are split into 50,000 training images and 10,000 test images. Both the datasets have 10 distinct classes. The mini-ImageNet dataset consists of 50,000 training images and 10,000 test images, evenly distributed across 100 classes. Every image has a size of 84x84x3.
6.2 Impact on representation learning
6.2.1 Methods
Proposed method. To investigate the impact of disentangling data representation on classification tasks, we divided the training processes into two stages: representation learning and classifier training. In the representation learning stage, we employed the LDM-based regularization method, which consists of one primary neural network for sample reconstruction and two auxiliary networks to estimate LDM values. For the MNIST dataset, the main neural network had the following architecture: D(512)-D(256)-D\(^*\)(100)-D(256)-D(512)-D(784). For the CIFAR10 dataset, the model architecture was defined as C(3x3,128,2)-C\(^*\)(3x3,512,2)-T(3x3,64,2)-T(3x3,32,2)-T(3x3,3,1). In this notation, D(N) denotes a dense layer with N neurons, C(\(a\times b,c,d\)) represents a convolutional layer with c filters of kernel size \(a\times b\) and a stride of d, and T(\(a\times b,c, d\)) denotes a transpose convolutional layer, sharing the identical parameter interpretations with convolutional layers. Except for the final layers of these models, which were activated by the hyperbolic tangent (tanh) function, all other layers utilized the Rectified Linear Unit (ReLU) function. Subsequently, by minimizing the Mean Squared Error (MSE) function augmented with the LDM regularization term as the loss measure (see Eq. (26)) for reconstruction, the resulting outputs from the concealed dense layer D\(^*\)(100) and convolutional layer C\(^*\)(3x3,512,2) were identified as the new representations of the data samples.
To compute the LDM value, two auxiliary networks, \(T_1\) and \(T_2\) (as specified in Eq. (31)), were required. These networks shared an identical architecture, configured as D(512)-D(256)-D(1), with each layer followed by the softplus activation function. Notably, as different features in the obtained representations by the convolutional layer may originate from the same filter, while LDM is defined as a measure among different base mappings, we have chosen to apply the LDM regularizer to the filters themselves, as explained in the section on the regularization method.
Compared methods. Two effective methods, \(\beta \)-VAE [2] and InfoGAN [3], were chosen as comparative methods at the representation learning stage due to their involvement in disentanglement. \(\beta \)-VAE is a modification of the variational autoencoder (VAE) framework that introduces an adjustable hyperparameter \(\beta \) to control the degree of disentanglement between learned factors. Similarly, InfoGAN extends the Generative Adversarial Network (GAN) framework with an information-theoretic approach, enabling it to learn disentangled representations. The concrete implementation details of these two methods can be found in their original papers, which will not be restated here. In addition to the two methods mentioned above, the supervised contrastive learning (SCL) [34] was also selected as a comparison method due to its ability to enhance clustering effects in the embedding space. The SCL method comprises three main components: a data augmentation module, an encoder network, and a projection network. The encoder network used to generate the representations is designed to be consistent with the representation learning component of the LDM method. All other aspects of the SCL method remain the same as described in the original paper.
In the classifier training stage, for our proposed methods, we constructed a fully connected neural network (FNN) for the MNIST dataset and a CNN for the CIFAR10 dataset, respectively. Specifically, the architecture of the FNN was configured as D(512)x3-D(256)x2-D(128)-D(10). The CNN architecture was defined as C(3x3,2048,1)-C(3x3,512,1)-C(3x3,256,1)-C(3x3,128,1)-C(3x3,64,1)-D(10). In both architectures, the final layers, responsible for the classification task, contained 10 neurons with softmax activation for the target classes. For the compared methods, since the representations learned by them are vectors, the same classifier FNN as applied for the MNIST dataset is adopted. Obviously, the overparameterization of these these deep architectures makes them more susceptible to overfitting.
Finally, in both the representation learning and classifier training stages, we employed the Adam optimization algorithm with a learning rate of 0.001. Training continued until reaching 5,000 iterations in the representation learning stage and 10,000 iterations in the classifier training stage. All the experiments were repeated five times to capture the average outcomes.
6.2.2 Experiment Results
Reduction of LDM
We initially conducted an investigation to determine whether the LDM value could be reduced through the application of the LDM-method during the representation learning process. We varied the balancing parameter \(\lambda \) in Eq. (26) from 0 to 2 in increments of 0.5. The average results of experiments conducted on the MNIST and CIFAR10 datasets are illustrated in Fig. 3. It is worth noting that the LDM value exhibits a decreasing trend as the number of iterations increases when \(\lambda > 0\). This observation suggests that the LDM-method actively promotes the reduction of LDM values within the trained mappings. In particular, when \(\lambda = 0\), the LDM value remains unchanged, staying close to zero and consistently higher than in other cases. With the increase in the value of \(\lambda \), the LDM value tends to become smaller over the same training duration.
Moreover, we are interested in whether solely minimizing the classical unsupervised total correlation term is sufficient to achieve a reduction in LDM values. We conducted experiments on the MNIST dataset by using the mutual information term in Eq. (24) as the regularizer and recorded the results in Fig. 4. From Fig. 4, we can observe that the class conditional mutual information follows a similar trend as the mutual information increases, suggesting that relying solely on total correlation is inadequate for reducing LDM values.
Effect of LDM
We have empirically verified that the regularization method indeed leads to a reduction in the LDM value during the representation learning stage. Next, we will compare the trained LDM method with \(\beta \)-VAE, SCL and InfoGAN, observing the impact of LDM by visulalizing the learned factors. Here, to test the robustness of new representations of samples to noise, we add Gaussian noise with a mean of 0 and a standard deviation of 0.1 to the original images (see Fig. 6). It’s important to note that prior to introducing the noise, the pixel values of the images have already been normalized to the range [-1, 1]. The experiment results are showed in Fig. 5, where the output representation of all methods has been reduced to 2 dimensions by using t-Distributed Stochastic Neighbor Embedding method [35] for ease of visualization. Furtherly, to quantify the effectiveness of factors, we employed the reciprocal of the F-statistic [36] from analysis of variance as a measure of separability for the new feature representation. It is
where a smaller value of RF indicates a higher degree of separability. The RF values for each method are summarized in Tab. 1.
Compared only with the disentanglement methods VAE and InfoGAN, as shown in Table 1, LDM achieves the lowest RF values when \(\lambda > 1\). However, LDM’s RF values are still higher than those of the SCL method, as the primary goal of SCL is to preserve clustering structure. Despite this, as shown in Fig. 5, LDM produces the best overall results, where, although SCL has the smallest RF values, it simultaneously exhibits severe mixing across several categories. Similar issues can be also observed with the other two methods. Based on these observations, it suggests that LDM is more effective at selecting factors that contribute to better classification.
Furthermore, we conducted an investigation into the classification accuracy of LDM methods with varying regularization weights. This exploration aimed to determine whether the improvement in LDM value correlates with an increase in accuracy and whether there exists a definitive relationship between the LDM value and generalization error during the classification learning stage. Notably, in this stage, the mapping from the initial image to its representation remains fixed, and the feature noise was added to the training images.
To facilitate the observation of overfitting phenomena, in addition to adding noise to the original images, we also conducted another experiment based on the second type of noise. This type of noise pertains to label noise, achieved by randomly assigning labels to a subset of training samples, resulting in a new training set with 20% label noise The experimental results are presented in Fig. 7. For the MNIST dataset, as depicted in Fig. 7(a), it is evident that in comparison to the case where \(\lambda = 0\) (i.e., no regularizer is applied), the classification accuracies improve significantly in all other cases, regardless of which type of noise is added. Furthermore, the gap between the classification accuracies in the training and test sets narrows following the application of the LDM regularizer. Similar experimental results can be observed for the CIFAR10 dataset, as reported in Fig. 7b.
Finally, the new representations of samples obtained by \(\beta \)-VAE, SCL and InfoGan are used as inputs to train the classifier, and the classiffcation accuracies are summarized in Table. 2. Additionally, for comparison, the classification results of LDM under \(\lambda =1\) are also recorded in the table. Clearly, we can see that the classification accuracy of the LDM method is the highest and exhibits better generalization compared to the other two methods.
6.3 As a Regularizer of Classifier
6.3.1 Methods
We also explored the effect of employing LDM directly as a regularization term for classification models, departing from the two-stage training process in the previous section involving representation learning and classification. The baselines included pretrained versions of Inception [37], MobileNet [38] and ResNet50 [39], all achieving state-of-the-art (SOTA) results on the ImageNet dataset. These three models served as the base models for our methods after removing their top layers. We then introduced a convolutional layer with 1024 channels and a stride of 1 at the bottom of the three models, applying LDM with a weight of 0.1 on this layer. Following this convolutional layer, global average pooling and classification layers were added, resulting in three LDM-based (LDM-) classification methods. Note that the settings of the auxiliary networks and other details within LDM remained consistent with those of the previous section. Additionally, by substituting LDM with the total covariance (TC) term, as well as using L1 norm and L2 norm regularization, we derived three types of classification methods: TC-based, L1-based, and L2-based.
6.3.2 Experiment Results
The experiments were conducted using the mini-ImageNet dataset, with the same type of feature noise added to the original input images during the testing phase. However, the standard deviation of the noise is set to 0.01. The results, as outlined in Table. 3, highlight that LDM achieves the highest accuracy and the smallest train-test accuracy gap across nearly all scenarios. Remarkably, the top-performing method, LDM-MobileNet, achieves an impressive 2.78-point increase compared to the suboptimal method. Moreover, it’s worth noting that TC-based and L1/L2 based methods do not consistently enhance performance. One possible explanation is that while TC-based methods encourage strengthening the independence among hidden neurons, they may also disrupt their intrinsic clustering structures.
7 Conclusion
In this paper, we delve into the upper bound of generalization error from an information perspective, which naturally leads to the derivation of a disentanglement measure, LDM, among the hidden units of Deep Neural Networks (DNNs). Importantly, we establish a theoretical connection between the proposed LDM metric and the generalization capacity of DNNs.
Building upon these insights, we design a regularization method that formulates the proposed LDM measure as a regularizer. Our experiments provide strong evidence that the application of this regularizer effectively reduces the value of LDM. Moreover, they offer experimental support for the existence of an inverse relationship between the defined LDM and the generalization capacity of DNNs, without compromising classification accuracy. In the future, we will further explore the impact of applying regularization to different layers, as layers represent data at different abstraction levels.
Data Availability
The data and materials used in this study are publicly available from the following sources: CIFAR10: https://www.cs.toronto.edu/ kriz/cifar.html, MNIST: http://yann.lecun.com/exdb/mnist/
Code Availability
The code used for analysis and experiments in this study is available upon request and can be obtained from the corresponding author
Abbreviations
- LDM::
-
Label-based disentanglement measure
- VAEs::
-
Variational autoencoders
- GANs::
-
Generative adversarial networks
- SCL::
-
Supervised contrastive learning
- RF::
-
Reciprocal of the F-statistic
- PDF::
-
Probability density function
- TC::
-
Total covariance
- KL-Divergence::
-
Kullback–Leibler divergence
- VC dimension::
-
Vapnik–Chervonenkis dimension
- IID::
-
Independent and identically distributed
- DNNs::
-
Deep neural networks
- MSE::
-
Mean squared error
- CNNs::
-
Convolutional neural networks
- FNN::
-
Fully connected neural network
- GANs::
-
Generative adversarial networks
- MI::
-
Mutual information
- C-MI::
-
Class-conditional mutual information.
References
Bengio Y, Courville A, Vincent P (2013) Representation learning: a review and new perspectives. IEEE Trans Pattern Anal Mach Intell 35(8):1798–1828
Higgins I, Matthey L, Pal A, Burgess C, Glorot X, Botvinick M, Mohamed S, Lerchner A (2016) Beta-vae: Learning basic visual concepts with a constrained variational framework. In: Proceedings of the international conference on learning representations (ICLR (Poster))
Chen X, Duan Y, Houthooft R, Schulman J, Sutskever I, Abbeel P (2016) Infogan: interpretable representation learning by information maximizing generative adversarial nets. Adv Neural Inf Process Syst (NeurIPS) 29:2180–2188
Bengio E, Thomas V, Pineau J, Precup D, Bengio Y (2017) Independently controllable features. arXiv:1703.07718
Brakel P, Bengio Y (2018) Learning independent features with adversarial nets for non-linear ica. arXiv:1710.05050
Hjelm RD, Fedorov A, Lavoie-Marchildon S, Grewal K, Bachman P, Trischler A, Bengio Y (2019)Learning deep representations by mutual information estimation and maximization. In: Proceedings of the international conference on learning representations (ICLR), pp. 1–17
Yang M, Liu F, Chen Z, Shen X, Hao J, Wang J (2021) Causalvae: Disentangled representation learning via neural structural causal models. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR), pp. 9593–9602
Larsen ABL, Sønderby SK, Larochelle H, Winther O (2016) Autoencoding beyond pixels using a learned similarity metric. In: Proceedings of the international conference on machine learning (ICML), pp. 1558–1566
Higgins I, Amos D, Pfau D, Racaniere S, Matthey L, Rezende D, Lerchner A (2018) Towards a definition of disentangled representations. arXiv:1812.02230
Lee H-Y, Tseng H-Y, Huang J-B, Singh M, Yang M-H (2018) Diverse image-to-image translation via disentangled representations. In: Proceedings of the European Conference on Computer Vision (ECCV), pp. 35–51
Wu J, Li X, Ao X, Meng Y, Wu F, Li J (2020) Improving robustness and generality of nlp models using disentangled representations. arXiv:2009.09587
Carvalho DS, Mercatali G, Zhang Y, Freitas A (2022) Learning disentangled representations for natural language definitions. arXiv:2210.02898
Cogswell M, Ahmed F, Girshick R, Zitnick L, Batra D (2016) Reducing overfitting in deep networks by decorrelating representations. In: Proceedings of the International Conference on Learning Representations (ICLR), pp. 1–12
Gu S, Hou Y, Zhang L, Zhang Y (2018) Regularizing deep neural networks with an ensemble-based decorrelation method. In: Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), pp. 2177–2183
Locatello F, Bauer S, Lucic M, Raetsch G, Gelly S, Schölkopf B, Bachem O (2019) Challenging common assumptions in the unsupervised learning of disentangled representations. In: Proceedings of the International Conference on Machine Learning (ICML), pp. 4114–4124
Grover A, Ermon S (2019) Uncertainty autoencoders: Learning compressed representations via variational information maximization. In: Proceedings of the International Conference on Artificial Intelligence and Statistics (ACAIS), pp. 2514–2524
Xu A, Raginsky M (2017) Information-theoretic analysis of generalization capability of learning algorithms. In: Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), pp. 2524–2533
Boucheron S, Bousquet O, Lugosi G(2005) Theory of classification: a survey of some recent advances. ESAIM: Probability and Statistics 9, 323–375
Kawaguchi K, Kaelbling LP, Bengio Y (2018) Generalization in deep learning. Mathematics of Deep Learning, Cambridge University Press . preprintavailable as: MIT-CSAIL-TR-2018-014, Massachusetts Institute of Technology
Brown G (2009) An information theoretic perspective on multiple classifier systems. In: Proceedings of the 8th International Workshop on Multiple Classifier Systems (MCS), pp. 344–353
Zhou Z-H, Li N (2010) Multi-information ensemble diversity. In: Proceedings of the 9th International Conference on Multiple Classifier Systems (MCS), pp. 134–144
Achille A, Soatto S (2018) Emergence of invariance and disentanglement in deep representations. J Mach Learn Res 19(1):1947–1980
Wang D, Dong Y, Li Y, Zi Y, Zhang Z, Li X, Xiong S (2021) Variational information bottleneck based regularization for speaker recognition. In: Proceedings of Interspeech, pp. 1054–1058
Cover TM, Thomas JA (2006) Elements Information Theory. Wiley-Interscience, Hoboken, NJ
Russo D, Zou J (2020) How much does your data exploration overfit? controlling bias via information usage. IEEE Trans Inf Theory 66(1):302–323
Massart P, Picard J (2007) Saint-Flour: Concentration Inequalities and Model Selection. Springer, Berlin, Heidelberg
Zhang C, Bengio S, Hardt M, Recht B, Vinyals O (2021) Understanding deep learning (still) requires rethinking generalization. Commun ACM 64(3):107–115
Belghazi MI, Rajeswar S, Baratin A, Hjelm D, Courville A (2018) Mine: Mutual information neural estimation. arXiv:1801.04062
Donsker MD, Varadhan S (1975) Asymptotic evaluation of certain markov process expectations for large time-iii. Commun Pure Appl Mathe 28(2):389–461
Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y (2014) Generative adversarial nets. In: Advances in neural information processing systems (NeurIPS), pp. 2672–2680
LeCun Y, Cortes C, Burges C (2010) Mnist handwritten digit database. AT &T Labs [Online]. Available: http://yann.lecun.com/exdb/mnist 2, 18
Krizhevsky A (2009) Learning multiple layers of features from tiny images. In: Proceedings of the international conference on computer vision (ICCV) (2009)
Krizhevsky A, Sutskever I, Hinton GE (2017) Imagenet classification with deep convolutional neural networks. Commun ACM 60(6):84–90
Khosla P, Teterwak P, Wang C, Sarna A, Tian Y, Isola P, Maschinot A, Liu C, Krishnan D (2020) Supervised contrastive learning 33:18661–18673
Cieslak MC, Castelfranco AM, Roncalli V, Lenz PH, Hartline DK (2020) t-distributed stochastic neighbor embedding (t-sne): A tool for eco-physiological transcriptomic analysis. Marine Genomics 51:100723
Montgomery DC, Runger GC (2010) Applied Statistics and Probability for Engineers. John Wiley & Sons, Hoboken, NJ
Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z (2016) Rethinking the inception architecture for computer vision. In: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pp. 2818–2826
Howard AG, Zhu M, Chen B, Kalenichenko D, Wang W, Weyand T, Andreetto M, Adam H (2017) Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv:1704.04861
Zhang Y, Wang C, Ling X, Deng W (2022) Learn from all: Erasing attention consistency for noisy label facial expression recognition. arXiv:2207.10299
Acknowledgements
Not applicable.
Funding
This work has received support from the National Natural Science Foundation of China (Project Number 62166016, 61876129), the Natural Science Foundation of Hainan Province (624MS039), the National Key R&D Program of China (2017YFE0111900).
Author information
Authors and Affiliations
Contributions
CZ and YH proposed the methodology and wrote the initial manuscript; DS reviewed the results and produced the final manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors affirm that they have no known competing financial interests or personal relationships that might have influenced the work reported in this paper.
Consent to Participate
All participants in this study provided informed consent to take part in the research.
Consent for Publication
Authors have given their consent for the publication of the research findings and related materials.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhang, C., Hou, Y. & Song, D. Label-Based Disentanglement Measure among Hidden Units of Deep Learning. Neural Process Lett 56, 252 (2024). https://doi.org/10.1007/s11063-024-11708-8
Accepted:
Published:
DOI: https://doi.org/10.1007/s11063-024-11708-8