A few remarks on recurrence relations for geometrically continuous piecewise Chebyshevian B-splines

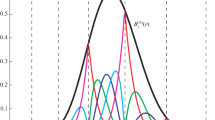
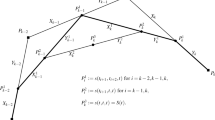
Abstract

This works complements a recent article (Mazure, J. Comp. Appl. Math. 219(2):457–470, 2008) in which we showed that T. Lyche’s recurrence relations for Chebyshevian B-splines (Lyche, Constr. Approx. 1:155–178, 1985) naturally emerged from blossoms and their properties via de Boor type algorithms. Based on Chebyshevian divided differences, T. Lyche’s approach concerned splines with all sections in the same Chebyshev space and with ordinary connections at the knots. Here, we consider geometrically continuous piecewise Chebyshevian splines, namely, splines with sections in different Chebyshev spaces, and with geometric connections at the knots. In this general framework, we proved in (Mazure, Constr. Approx. 20:603–624, 2004) that existence of B-spline bases could not be separated from existence of blossoms. Actually, the present paper enhances the powerfulness of blossoms in which not only B-splines are inherent, but also their recurrence relations. We compare this fact with the work by G. Mühlbach and Y. Tang (Mühlbach and Tang, Num. Alg. 41:35–78, 2006) who obtained the same recurrence relations via generalised Chebyshevian divided differences, but only under some total positivity assumption on the connexion matrices. We illustrate this comparison with splines with four-dimensional sections. The general situation addressed here also enhances the differences of behaviour between B-splines and the functions of smaller and smaller supports involved in the recurrence relations.