Abstract
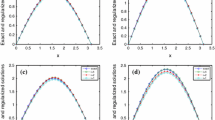
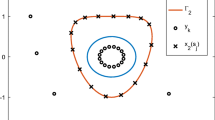
Based on a mathematical model of laser beams, we present a spectral Galerkin method for solving a Cauchy problem of the Helmholtz equation in a rectangle, where the Cauchy data pairs are given at y = 0 and boundary data are for x = 0 and x = π. The solution is sought in the interval 0 < y < 1. The spectral Galerkin method is considered as a regularization method. We then perform an analysis on the error bound for this method. For illustration, several numerical experiments are constructed to demonstrate the feasibility and efficiency of the proposed method.
Similar content being viewed by others
References
Alessandrini, G.: Stable determination of a crack from boundary measurements. Proc. Roy. Soc. Edinburgh Sect. A 123, 961–984 (1993)
Cheng, J., Yamamoto, M.: Unique continuation on a line for harmonic functions. Inverse Probl. 14, 869–882 (1998)
Colli-Franzone, P., Guerri, L., Tentoni, S., Viganotti, C., Baruffi, S., Spaggiari, S., Taccardi, B.: A mathematical procedure for solving the inverse potential problem of electrocardiography. Analysis of the time-space accuracy from in vitro experimental data. Math. Biosci. 77, 353–396 (1985)
Murio, D.A.: The Mollification Method and the Numerical Solution of Ill-Posed Problems. Wiley, Interscience Division, New York, New York (1993)
Eldén, L., Berntsson, F., Regińska, T.: Wavelet and Fourier methods for solving the sideways heat equation. SIAM J. Sci. Comput. 21(6), 2187–2205 (2000)
Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems. Kluwer Academic Publisher, Dordrecht Boston London (1996)
Hào, D.N., Hien, P.M.: Stability results for the Cauchy problem for the Laplace equation in a strip. Inverse Probl. 19, 833–844 (2003)
Hào, D.N., Lesnic, D.: The Cauchy for Laplace’s equation via the conjugate gradient method. IMA J. Appl. Math. 65, 199–217 (2000)
Hofmann, B.: Approximate source conditions in Tikhonov-Phillips regularization and consequences for inverse problems with multiplication operators. Math. Methods Appl. Sci. 29, 351–371 (2006)
Hohage, T.: Regularization of exponentially ill-posed problems. Numer. Funct. Anal. Optim. 21, 439–464 (2000)
Hon, Y.C., Wei, T.: Backus-Gilbert algorithm for the Cauchy problem of laplace equation. Inverse Probl. 17, 261–271 (2001)
Mahale, P., Nair, M.T.: General source conditions for nonlinear ill-posed equations. Numer. Funct. Anal. Optim. 28, 111–126 (2007)
Marin, L., Elliott, L., Heggs, P.J., Ingham, D.B., Lesnic, D., Wen, X.: An alternating iterative algorithm for the Cauchy problem associated to the Helmholtz equation. Comput. Meth. Appl. Mech. Eng. 192, 709–722 (2003)
Marin, L.: A meshless method for the numerical solution of the Cauchy problem associated with three-dimensional Helmholtz-type equations. Appl. Math. Comput. 165(2), 355–374 (2005)
Marin, L., Elliott, L., Heggs, P.J., Ingham, D.B., Lesnic, D., Wen, X.: BEM solution for the Cauchy problem associated with Helmholtz-type equations by the Landweber method. Eng. Anal. Bound. Elem. 28, 1025–1034 (2004)
Marin, L., Elliott, L., Heggs, P.J., Ingham, D.B., Lesnic, D., Wen, X.: Conjugate gradient-boundary element solution to the Cauchy problem for Helmholtz-type equations. Comput. Mech. 31, 367–377 (2003)
Marin, L., Lesnic, D.: The method of fundamental solutions for the Cauchy problem associated with two-dimensional Helmholtz-type equations. Comput. Struct. 83, 267–278 (2005)
Marin, L., Elliott, L., Heggs, P.J., Ingham, D.B., Lesnic, D., Wen, X.: Comparison of regularization methods for solving the Cauchy problem associated with the Helmholtz equation. Int. J. Numer. Methods Eng. 60(11), 1933–1947 (2004)
Mathé, P., Pereverzev, S.: Geometry of ill-posed problems in variable Hilbert scales. Inverse Probl. 19, 789–803 (2003)
Nair, M.T., Tautenhahn, U.: Lavrentiev regularization for linear ill-posed problems under general source conditions. Z. Anal. Anw. 23, 167–185 (2004)
Payne, L.E.: Bounds in the Cauchy problem for the Laplace’s equation. Arch. Ration. Mech. Anal. 5, 35–45 (1960)
Qian, Z., Fu, C.L., Xiong, X.T.: Fourth-order modified method for the Cauchy problem for the Laplace equation. J. Comput. Appl. Math. 192, 205–218 (2006)
Qin, H.H., Wei, T.: Modified regularization method for the Cauchy problem of the Helmholtz equation. Appl. Math. Model. 33, 2334–2348 (2009)
Reinhardt, H.J., Han, H., Hào, D.N.: Stability and regularization of a discrete approximation to the Cauchy problem of Laplace’s equation. SIAM J. Numer. Anal. 36, 890–905 (1999)
Tautenhahn, U.: Optimality for linear ill-posed problems under general source conditions. Numer. Funct. Anal. Optim. 19, 377–398 (1998)
Tautenhahn, U.: On the method of Lavrentiev regularization for nonlinear ill-posed problems. Inverse Probl. 18, 191–207 (2002)
Tikhonov, A.N., Arsenin, V.Y.: Solutions of Ill-Posed Problems. Winston and Sons, Washington, D. C. (1977)
Wei, T., Hon, Y.C., Ling, L.: Method of fundamental solutions with regularization techniques for Cauchy problems of elliptic operators. Eng. Anal. Bound. Elem. 31(4), 373–385 (2007)
Xiong, X.T.: Central difference regularization method for the Cauchy problem of Laplace’s equation. Appl. Math. Comput. 181, 675–684 (2006)
Xiong, X.T., Fu, C.L., Cheng, J.: Spectral regularization methods for solving a sideways parabolic equation within the framework of regularization theory. Math. Comput. Simul. 79, 1668–1678 (2009)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Xiong, X., Zhao, X. & Wang, J. Spectral Galerkin method and its application to a Cauchy problem of Helmholtz equation. Numer Algor 63, 691–711 (2013). https://doi.org/10.1007/s11075-012-9648-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-012-9648-9