Skip to main content
SpringerLink
Log in

Operator compact method of accuracy two in time and four in space for the solution of time dependent Burgers-Huxley equation

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

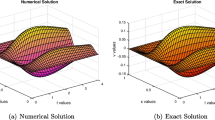
In this paper, we propose a new two-level implicit compact operator method of order two in time (t) and four in space (x) for the solution of time dependent Burgers-Huxley equation with appropriate initial and boundary conditions. The presence of Reynolds number and nonlinear terms in the problem leads to severe difficulties in the numerical approximation. To overcome such difficulties, the method based on operators is constructed. We use only 3-spatial grid points and the obtained tridiagonal nonlinear system has been solved by Newton’s iteration method. The test problems considered in the literature have been discussed to demonstrate the strength and utility of the proposed method. The computed numerical solutions are in good agreement with the exact solutions. We show that the proposed method enables us to obtain high accuracy solution for high Reynolds number.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wang, X.: Nerve propagation and wall in liquid crystals. Phys. Lett. 112A, 402–406 (1985)

    Article  Google Scholar 

  2. Wang, X.Y., Zhu, Z.S., Lu, Y.K.: Solitary wave solutions of the generalized Burgers-Huxley equation. J. Phys. A: Math. Gen. 23, 271–274 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  3. Burgers, J.M.: A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171–199 (1948)

    Article  MathSciNet  Google Scholar 

  4. Dai, W., Chen, C.J.: Finite analytic explicit scheme for viscous Burger’s equation, pp 549–553. Proceedings of ASCE Engineering Mechanics Specialty Conference, Columbus (1991)

    Google Scholar 

  5. Estevez, P.G.: Non-classical symmetries and the singular modified the Burger’s and Burgers-Huxley equation. J. Phys. A-Math. Gen. 27, 2113–2127 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  6. Efimova, O.Y.U., Kudryashov, N.A.: Exact solutions of the Burgers-Huxley equation. J. Appl. Math. Mech. 68, 413–420 (2004)

    Article  MathSciNet  Google Scholar 

  7. Ismail, H.N.A., Raslan, K., Rabboh, A.A.A.: Adomian decomposition method for Burgers- Huxley and Burgers-Fisher equations. Appl. Math. Comput. 159, 291–301 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  8. Hashim, I., Noorani, M.S.M., Al-Hadidi, M.R.S.: Solving the generalized Burgers-Huxley equation using the adomian decomposition method. Math. Comput. Model. 43, 1404–1411 (2006)

    Article  MATH  Google Scholar 

  9. Hashim, I., Noorani, M.S.M., Batiha, B.: A note on the adomian decomposition method for the generalized Huxley equation. Appl. Math. Comput. 181, 1439–1445 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  10. Deng, X.: Travelling wave solutions for the generalized Burgers-Huxley equation. Appl. Math. Comput. 204, 733–737 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  11. Wazwaz, A.M.: Analytic study of Burger’s, Fisher, Huxley equations and combined forms of these equations. Appl. Math. Comput. 195, 1209–1216 (2008)

    Google Scholar 

  12. Bataineh, A.S., Noorani, M.S.M., Hashim, I.: Analytical treatment of generalized Burgers-Huxley equation by homotopy analysis method. Bull. Malaya Math. Sci. Soc. 32, 233–243 (2009)

    MATH  MathSciNet  Google Scholar 

  13. Molabahrami, A., Khami, F.: The homotopy analysis method to solve the Burgers-Huxley equation. Nonlinear Anal. Real World Appl. 10, 589–600 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  14. Gao, H., Zhao, R.: New exact solutions to the generalized Burgers-Huxley equation. Appl. Math. Comput. 217, 1598–1603 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  15. Griffiths, G.W., Schiesser, W.E.: Travelling Wave Analysis of Partial Differential Equations. Academic Press (2012)

  16. Jr, A.C.: Reynolds, Convergent finite difference schemes for non-linear parabolic equations. SIAM. J. Numer. Anal. 9, 523–533 (1972)

    Article  MathSciNet  Google Scholar 

  17. Jain, M.K., Jain, R.K., Mohanty, R.K.: High order difference methods for system of 1-D non-linear parabolic partial differential equations. Int. J. Comput. Math. 37, 105–112 (1990)

    Article  MATH  Google Scholar 

  18. Jain, M.K., Jain, R.K., Mohanty, R.K.: A fourth order difference method for the one dimensional general quasi-linear parabolic partial differential equation. Numer. Meth. Partial Diff. Eqn. 6, 311–319 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  19. Mohanty, R.K.: An O(k 2+h 4) finite difference method for one space Burgers’ equation in polar coordinates. Numer. Meth. Partial Diff. Eqn. 12, 579–583 (1996)

    Article  MATH  Google Scholar 

  20. Mohanty, R.K., Jain, M.K., Kumar, D.: Single cell finite difference approximations of O(kh 2+h 4) for (∂ u/∂ x) for one space dimensional non-linear parabolic equations. Numer. Meth. Partial Diff. Eqn. 16, 408–415 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  21. Mohanty, R.K., Jain, M.K.: High accuracy cubic spline alternating group explicit methods for 1D quasi-linear parabolic equations. Int. J. Comput. Math. 86, 1556–1571 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  22. Mohanty, R.K., Talwar, J.: SWAGE algorithm for the cubic spline solution of nonlinear viscous Burgers’ equation on a geometric mesh. Results Phys. 03, 195–204 (2013)

    Article  Google Scholar 

  23. Talwar, J., Mohanty, R.K.: A new modified group explicit iterative method for the numerical solution of time dependent viscous Burgers’ equation. Int. J. Model. Simul. Sci. Comput. 05(2014). ID: 1350029

  24. Javidi, M.: A numerical solution of the generalized Burgers-Huxley equation by pseudospectral method and darvishi’s preconditioning. Appl. Math. Comput. 175, 1619–1628 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  25. Javidi, M.: A numerical solution of the generalized Burgers-Huxley equation by spectral collocation method. Appl. Math. Comput. 178, 338–344 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  26. Javidi, M., Golbabai, A.: A new domain decomposition algorithm for generalized Burgers-Huxley equation based on chebyshev polynomials and preconditioning. Chaos Soliton Fractals 39, 849–857 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  27. Javidi, M.: A modified Chebyshev pseudospectral domain decomposition algorithm for the generalized Burgers-Huxley equation. Comp. Math. Applics. 62, 3366–3377 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  28. Batiha, B., Noorani, M.S.M., Hashim, I.: Application of variational iteration method to the generalized Burgers-Huxley equation. Chaos Solitons Fractals 36, 660–663 (2008)

    Article  MATH  Google Scholar 

  29. Khattak, A.J.: A computational meshless method for the generalized Burgers-Huxley equation. Appl. Math. Model. 33, 3718–3729 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  30. Gupta, V., Kadalbajoo, M.K.: A singular perturbation approach to solve Burgers-Huxley equation via monotone finite difference scheme on layer adaptive mesh. Commun. Nonlinear Sci. Numer. Simul. 16, 1825–1844 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  31. Diaz, J.E.M., Ramirez, J.R., Villa, J.: The numerical solution of a generalized Burgers-Huxley equation through a conditionally boundaed and symmetry-preserving method. Comp. Math. Applics. 61, 3330–3342 (2011)

    Article  MATH  Google Scholar 

  32. Bratsos, A.G.: A fourth order improved numerical scheme for the generalized Burgers-Huxley equation. Am. J. Comput. Math. 1, 152–158 (2011)

    Article  Google Scholar 

  33. Dehghan, M., Saray, B.N., Lakestani, M.: Three methods based on the interpolation scaling functions and the mixed collocation finite difference schemes for the numerical solution of the nonlinear generalized Burgers-Huxley equation. Math. Comput. Model. 55, 1129–1142 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  34. Zhou, S., Cheng, X.: A linearly semi-implicit compact scheme for the Burgers-Huxley equation. Int. J. Comput. Math. 88, 795–804 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  35. Sari, M., Gurarslan, G., Zeytinoglu, A.: High-order finite difference schemes for numerical solutions of the generalized Burgers-Huxley equation. Numer. Meth. Partial Diff. Eq. 27, 1313–1326 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  36. Mohammadi, R.: B-spline collocation algorithm for numerical solution of the generalized Burger’s-Huxley equation. Numer. Meth. Partial Diff. Eq. 29, 1173–1191 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  37. Kelly, C.T.: Iterative methods for linear and nonlinear equations. SIAM publication, Philadelphia (1995)

    Book  Google Scholar 

  38. Hageman, L.A., Young, D.M.: Applied Iterative Methods. Dover Publication (2012)

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, South Asian University, Akbar Bhawan, Chanakyapuri, New Delhi, 110021, India

    R. K. Mohanty

  2. Department of Mathematics and Statistics, Louisiana Tech University, Ruston, LA, 71272, USA

    Weizhong Dai & Don Liu

Authors
  1. R. K. Mohanty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weizhong Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Don Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. K. Mohanty.

Additional information

Supported by the United States-India Educational Foundation under the 2013 Fulbright-Nehru Senior Research Fellowship Program and partially supported by the National Science Foundation (NSF EPS-1003897)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mohanty, R.K., Dai, W. & Liu, D. Operator compact method of accuracy two in time and four in space for the solution of time dependent Burgers-Huxley equation. Numer Algor 70, 591–605 (2015). https://doi.org/10.1007/s11075-015-9963-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-015-9963-z

Keywords

Mathematics subject classifications (2010)

Search

Navigation