Abstract
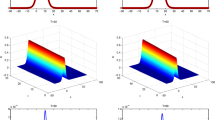
In this paper, a new high-order energy-preserving scheme is proposed for the modified Korteweg-de Vries equation. The proposed scheme is constructed by using the Hamiltonian boundary value methods in time, and Fourier pseudospectral method in space. Exploiting this method, we get second-order and fourth-order energy-preserving integrators. The proposed schemes not only have high accuracy, but also exactly conserve the total mass and energy in the discrete level. Finally, single solitary wave and the interaction of two solitary waves are presented to illustrate the effectiveness of the proposed schemes.
Similar content being viewed by others
References
Zabusky, N.J., Kruskal, M.D.: Interaction of solitons in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15(6), 240–243 (1965)
Drazin, P.G., Johnson, R.S.: Solitons: an introduction. Cambridge University Press (1996)
Miura, R.M.: The Korteweg-de Vries equation: a survey of results. SIAM Rev. 19(4), 412–459 (1977)
Ito, M.: An extension of nonlinear evolution equations of the K-dV (mK-dV) type to higher orders. J. Physical Soc. Japan 49(2), 771–778 (1980)
Wadati, M.: The exact solution of the modified Korteweg-de Vries equation. J. Physical Soc. Japan 32, 1681–1687 (1972)
Miura, R.M., Gardner, C.S., Kruskal, M.D.: Korteweg-de Vries equation and generalization. II. Existence of conservation laws and constants of motion. J. Math. Phys. 9(8), 1204–1209 (1968)
Bridges, T.J.: Multi-symplectic structures and wave propagation. Math. Proc. Camb. Philos. Soc. 121(1), 147–190 (1997)
Gonzalez, O.: Time integration and discrete Hamiltonian systems. J. Nonlinear Sci. 6(5), 449–467 (1996)
McLachlan, R.I., Quispel, G.R.W., Robidoux, N.: Geometric integration using discrete gradients. Philos. Trans. R. Soc. 357(1754), 1021–1045 (1999)
Hulme, B.L.: One-step piecewise polynomial Galerkin methods for initial value problems. Math. Comput. 26(118), 415–426 (1972)
Wang, Q.X., Zhang, Z.Y., Zhang, X.H., Zhu, Q.Y.: Energy-preserving finite volume element method for the improved Boussinesq equation. J. Comput. Phys. 270, 58–69 (2014)
Iavernaro, F., Pace, B.: S-stage trapezoidal methods for the conservation of Hamiltonian functions of polynomial type. AIP Conf. Proc. 936(1), 603–606 (2007)
Iavernaro, F., Pace, B.: Conservative block-boundary value methods for the solution of polynomial Hamiltonian systems. AIP Conf. Proc. 1048(1), 888–891 (2008)
Quispel, G.R.W., McLaren, D.I.: A new class of energy-preserving numerical integration methods. J. Phys. A. Math. Theor. 41(4), 045206 (2008)
Iavernaro, F., Trigiante, D.: High-order symmetric schemes for the energy conservation of polynomial Hamiltonian problems. J. Numer. Anal. Ind. Appl. Math. 4(1–2), 87–101 (2009)
Brugnano, L., Iavernaro, F., Trigiante, D.: Numerical solution of ODEs and the columbus’s egg: three simple ideas for three difficult problems. Math. Eng. Sci. Aerosp. 1(4), 407–426 (2010)
Brugnano, L., Iavernaro, F., Trigiante, D.: A note on the efficient implementation of Hamiltonian BVMs. J. Comput. Appl. Math. 236(3), 375–383 (2011)
Brugnano, L., Iavernaro, F., Trigiante, D.: A simple framework for the derivation and analysis of effective one-step methods for ODEs. Appl. Math. Comput. 218(17), 8475–8485 (2012)
Brugnano, L., Iavernaro, F., Trigiante, D.: Analysis of Hamiltonian boundary value methods (HBVMs): a class of energy-preserving Runge-Kutta methods for the numerical solution of polynomial Hamiltonian systems. Commun. Nonlinear Sci. Numer. Simul. 20(3), 650–667 (2015)
Brugnano, L., Iavernaro, F., Trigiante, D.: Hamiltonian boundary value methods (Energy preserving discrete line integral methods). J. Numer. Anal. Ind. Appl. Math. 5(1–2), 17–37 (2010)
Brugnano, L., Frasca Caccia, G., Iavernaro, F.: Energy conservation issues in the numerical solution of the semilinear wave equation. Appl. Math. Comput. 270, 842–870 (2015)
Li, S., Vu-Quoc, L.: Finite difference calculas invarient structure of a class of algorithms for the nonlinear Klein-Gordon equation. SIAM J. Numer. Anal. 32(6), 1839–1875 (1995)
Gardner, L.R.T., Gardner, G.A., Geyikli, T.: Solitary wave solutions of the MKdv − equation. Comput. Methods Appl. Mech. Eng. 124(4), 321–333 (1995)
Zheng, C.X.: Numerical simulation of a modified KdV equation on the whole real axis. Numer. Math. 105(2), 315–335 (2006)
Gorria, C., Alejo, M.A., Vega, L.: Discrete conservation laws and the convergence of long time simulations of the mkdv equation. J. Comput. Phys. 235, 274–285 (2013)
Raslan, K.R., Baghdady, H.A.: New algorithm for solving the modified Korteweg-de Vries (mKdV) equation. J. Res. Rev. Appl. Sci. 18(1), 59–64 (2014)
Bona, J.L., Dougalis, V.A., Karakashian, O.A., McKinney, W.R.: Conservative, high-order numerical schemes for the generalized Korteweg-de Vries equation. Philos. Trans. R. Soc. 351(1695), 107–164 (1995)
Cui, Y.F., Mao, D.K.: Numerical method satisfying the first two conservation laws for the Korteweg-de Vries equation. J. Comput. Phys. 227(1), 376–399 (2007)
Bona, J.L., Chen, H., Karakashian, O., Xing, Y.: Conservative, discontinuous-Galerkin methods for the generalized Korteweg-de Vries equation. Math. Comput. 82(283), 1401–1432 (2013)
Yi, N.Y., Huang, Y.Q., Liu, H.L.: A direct discontinuous Galerkin method for the generalized Korteweg-de Vries equation Energy conservation and boundary effect. J. Comput. Phys. 242, 351–366 (2013)
Brugnano, L., Iavernaro, F.: Line integral methods for conservative problems. series: monographs and research notes in mathematics. Chapman and Hall/CRC, Boca Raton (2016). ISBN 9781482263848
Chen, J.B., Qin, M.Z.: Multi-symplectic Fourier pseudospectral method for the nonlinear Schrödinger equation. Electron. Trans. Numer. Anal. 12, 193–204 (2001)
Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.: Spectral methods in fluid dynamics. Springer, New York (1988)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yan, JL., Zhang, Q., Zhang, ZY. et al. A new high-order energy-preserving scheme for the modified Korteweg-de Vries equation. Numer Algor 74, 659–674 (2017). https://doi.org/10.1007/s11075-016-0166-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-016-0166-z