Skip to main content
SpringerLink
Log in

Analysis and numerical simulation for a class of time fractional diffusion equation via tension spline

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

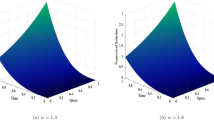
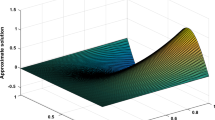
The numerical solution for a class of time fractional diffusion equation via tension spline is studied. Time fractional derivative is considered in the Caputo sense. The numerical method is constructed by means of the Crank-Nicolson method and is proven to be conditionally stable. Convergence analysis is also discussed by using the Fourier series method. Numerical evidences are given to prove the efficiency of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Al-Shibani, F., Ismail, A.: Compact Crank-Nicolson and Du Fort—Frankel method for the solution of the time fractional diffusion equation. Int. J. Comp. Meth. 12(6), 1–31 (2015)

    MathSciNet  MATH  Google Scholar 

  2. Atangana, A., Alkahtani, B.S.T.: Extension of the resistance, inductance, capacitance electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 7(6), 1–6 (2015)

    Article  Google Scholar 

  3. Atangana, A.: On the new fractional derivative and application to nonlinear Fisher’s reaction-diffusion equation. Appl. Math. Comput. 273, 948–956 (2016)

    MathSciNet  Google Scholar 

  4. Brociek, R.: Implicit finite difference method for time fractional heat equation with mixed boundary conditions. Matematyka Stosowana/Politechnika Slaska, Zeszyty Naukowe (2014)

    Google Scholar 

  5. Bu, W., Tang, Y., Yang, J.: Galerkin finite element method for two–dimensional Riesz space fractional diffusion equations. J. Comput. Phy. 276, 26–38 (2014)

    Article  MathSciNet  Google Scholar 

  6. Chen, C.M., Liu, F., Turner, I., Anh, V.: A Fourier method for the fractional diffusion equation describing sub–diffusion. J. Comput. Phy. 227, 886–897 (2007)

    Article  MathSciNet  Google Scholar 

  7. Guo, B., Xueke, P., Fenghui, H.: Fractional partial differential equations and their numerical solutions. World Scientific, Singapore (2015)

    Book  Google Scholar 

  8. Hashemi, M., Baleanu, D., Parto-Haghighi, M., Darvishi, E.: Solving the time fractional diffusion equation using a lie group integrator. Therm. Sci. 19(suppl. 1), 77–83 (2015)

    Article  Google Scholar 

  9. Jafari, H., Daftardar-Gejji, V.: Solving linear and nonlinear fractional diffusion and wave equations by Adomian decomposition. Appl. Math. Comput. 180, 488–497 (2006)

    MathSciNet  MATH  Google Scholar 

  10. Karatay, I., Kale, N., Bayramoglu, S.R.: A new difference scheme for time fractional heat equations based on the Crank-Nicholson method. Fract. Calc. Appl. Anal. 16(4), 892–910 (2013)

    Article  MathSciNet  Google Scholar 

  11. Kilbas, A.A., Srivastava, H.M., Trujillo: Theory and Applications of Fractional Differential Equations. Elsevier, North-Holland (2006)

    MATH  Google Scholar 

  12. Li, C., Zhao, Z., Chen, Y.: Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion. Comput. Math. Appl. 62, 855–875 (2011)

    Article  MathSciNet  Google Scholar 

  13. Li, M., Huang, C., Wang, P.: Galerkin finite element method for nonlinear fractional Schrödinger equations. Numer. Algor. 74, 499–525 (2017)

    Article  Google Scholar 

  14. Parvizi, M., Eslahch, M.R., Dehghan, M.: Numerical solution of fractional advection-diffusion equation with a nonlinear source term. Numer. Algor. 68, 601–629 (2015)

    Article  MathSciNet  Google Scholar 

  15. Podlubny, L.: Fractional differential equations. Academic Press, New York (1999)

    MATH  Google Scholar 

  16. Sweilam, N.H., Moharram, H., Abdel Moniem, N.K., Ahmed, S.: A parallel Crank–Nicolson finite difference method for time-fractional parabolic equation:. J. Numer. Math. 22(4), 363–382 (2014)

    Article  MathSciNet  Google Scholar 

  17. Wang, S., Xu, M., Li, X.: Green’s function of time fractional diffusion equation and its applications in fractional quantum mechanics. Nonlinear Anal. 10, 1081–1086 (2009)

    Article  MathSciNet  Google Scholar 

  18. Wei, L.: Stability and convergence of a fully discrete local discontinuous Galerkin method for multi–term time fractional diffusion equations. Numer. Algor. 76(3), 695–707 (2017)

    Article  MathSciNet  Google Scholar 

  19. Wu, G., Lee, E.W.M.: Fractional variational iteration method and its application. Phys. Lett. A 374, 2506–2509 (2010)

    Article  MathSciNet  Google Scholar 

  20. Zhang, P., Hai, P.: A second-order compact difference scheme for the fourth-order fractional sub-diffusion equation. Numer. Algor. 76(2), 573–598 (2017)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to express their sincere thanks and gratitude to the editors and the anonymous referees for their valuable comments and suggestions in the improvement of the manuscript.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology, Kurukshetra, Haryana, 136 119, India

    A. S. V. Ravi Kanth & Deepika Sirswal

Authors
  1. A. S. V. Ravi Kanth
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Deepika Sirswal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. S. V. Ravi Kanth.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kanth, A.S.V.R., Sirswal, D. Analysis and numerical simulation for a class of time fractional diffusion equation via tension spline. Numer Algor 79, 479–497 (2018). https://doi.org/10.1007/s11075-017-0447-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-017-0447-1

Keywords

Mathematics Subject Classification (2010)

Search

Navigation