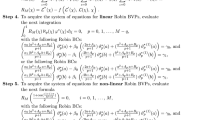Abstract
The aim of this manuscript is to investigate an accurate discretization method to solve the one-, two-, and three-dimensional highly nonlinear Bratu-type problems. By discretization of the nonlinear equation via a fourth-order nonstandard compact finite difference formula, the considered problem is reduced to the solution of a highly nonlinear algebraic system. To solve the derived nonlinear system, a modified nonlinear solver is used. The new scheme is accurate, fast, straightforward and very effective to find the lower and upper branches of the Bratu’s problem. Numerical simulations and comparative results for the one-, two-, and three-dimensional cases verify that the new technique is easy to implement and more accurate than the other existing methods in the literature.
Similar content being viewed by others
References
Bratu, G.: Sur les équations intégrales non linéaires. Bull. Math. Soc. France 42, 113–142 (1914)
Chandrasekhar, S.: Introduction to the Study of Stellar Structure. Dover, New York (1967)
Jacobsen, J., Schmitt, K.: The Liouville-Bratu-Gelfand problem for radial operators. J. Differential Equations 184, 283–298 (2002)
Mohsen, A.: A simple solution of the Bratu problem. Comp. Math. App. 67, 26–33 (2014)
Buckmire, R.: Applications of Mickens finite differences to several related boundary value problems. Advances in the Applications of Nonstandard Finite Difference Schemes 47–87 (2005)
Khuri, S.: A new approach to Bratu’s problem. Appl. Math. Comput. 147(1), 131–136 (2004)
Caglar, H., Caglar, N., Ozer, M., Valaristos, A., Anagnostopoulos, A.N.: B-spline method for solving Bratu’s problem. Int. J. Comput. Math. 87(8), 1885–1891 (2010)
Boyd, J.: Chebychev polynomial expansions for simultaneous approximation of two branches of a function with application of the one-dimensional Bratu equation. Appl. Math. Comput. 142, 189–200 (2003)
Boyd, J.P.: An analytical and numerical study of the two-dimensional Bratu equation. J. Sci. Comput. 1, 183–206 (1986)
Deeba, E., Khuri, S., Xie, S.: An algorithm for solving boundary value problems. J. Comput. Phys. 159, 125–138 (2000)
Aksoy, Y., Pakdemirli, M.: New perturbation iteration solutions for Bratutype equations. Comput. Math. Appl. 59(8), 2802–2808 (2010)
Syam, M., Hamdan, A.: An efficient method for solving Bratu equation. Appl. Math. Comput. 176, 704–713 (2006)
Syam, M.I., Attili, B.: Weighted residual method for obtaining positive solutions of two-point nonlinear boundary value problems. Appl. Math. Comput. 176, 775–784 (2006)
Abbasbandy, M.H.S., Liu, C.: The lie-group shooting method for solving the bratu equation. Commun. Nonlinear Sci. Numer. Simul. 16, 4238–4249 (2011)
Das, N., Singh, R., Wazwaz, A., Kumar, J.: An algorithm based on the variational iteration technique for the Bratu-type and the Lane-Emden problems. J. Math. Chem. 54, 527–551 (2016)
Motsa, S.S., Sibanda, P.: Some modifications of the quasilinearization method with higher-order convergence for solving nonlinear BVPs. Numer. Algor. 63(3), 399–417 (2013)
Mohsen, A.: On the integral solution of the one-dimensional Bratu problem. J. Comput. Appl. Math. 251, 61–66 (2013)
Liu, X., Zhou, Y., Wang, X., Wang, J.: A wavelet method for solving a class of nonlinear boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 18, 1939–1948 (2013)
Yang, Z., Shijun, L.: A HAM-based wavelet approach for nonlinear partial differential equations: two dimensional Bratu problem as an application. Commun. Nonlinear Sci. Numer. Simul. 53, 249–262 (2017)
Saeed, U., Rehman, M.: Wavelet-galerkin quasilinearization method for nonlinear boundary value problems. Abstr. Appl. Anal. (2014):868934. https://doi.org/10.1155/2014/868934 (2014)
Ullah, M.Z., Serra-Capizzano, S., Ahmad, F.: An efficient multi-step iterative method for computing the numerical solution of systems of nonlinear equations associated with odes. Appl. Math. Comput. 250, 249–259 (2015)
Doha, E., Bhrawy, A., Baleanu, D., Hafez, R.: Efficient Jacobi-Gauss collocation method for solving initial value problems of Bratu type. Comput. Math. Math. Phys. 53(9), 1292–1302 (2013)
Chan, T., Keller, H.B.: Arc-length continuation and multi-grid techniques for nonlinear elliptic eigenvalue problems. SIAM J. Sci. Stat. Comput. 3, 173–194 (1984)
Hackbusch, W.: Comparison of different multi-grid variants for nonlinear equations. ZAMM Z. Angew. Math. Mech. 72, 148–151 (1992)
Rashidinia, J., Maleknejad, K., Taheri, N.: Sinc-galerkin method for numerical solution of the Bratu’s problems. Numer. Algor. 62, 1–11 (2013)
Zarebnia, M., Sarvari, Z.: Parametric spline method for solving Bratu’s problem. Int. J. Nonlin. Sci. 14, 3–10 (2012)
Jalilian, R.: Non-polynomial spline method for solving Bratu’s problem. Comput. Phys. Commun. 181, 1868–187 (2010)
Temimi, H., Ben-Romdhane, M.: An iterative finite difference method for solving Bratu’s problem. J. Comput. Appl. Math. 292, 76–82 (2016)
Kumar, M., Yadav, N.: Numerical solution of Bratu’s problem using multilayer perceptron Neural Network method. Natl. Acad. Sci. Lett. 38(5), 425–428 (2015)
Li, S., Liao, S.J.: An analytic approach to solve multiple solutions of a strongly nonlinear problem. Appl. Math. Comput. 169, 854–865 (2005)
Xu, Y., Li, X., Zhang, L.: The particle swarm shooting method for solving the Bratu’s problem. Journal of Algorithms & Computational Technology 9(3), 291–302 (2014)
Odejide, S., Aregbesola, Y.: A note on two-dimensional Bratu problem. Kragujevac J. Math. 29, 49–56 (2006)
Lele, S.: Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42 (1992)
Mickens, R.E.: Nonstandard Finite Difference Models of Differential Equations. World Scientific, Singapore (1994)
Mickens, R.E.: Applications of Nonstandard Finite-Difference Schemes. World Scientific, River Edge (2000)
Ames, W.F.: Numerical Methods for Partial Differential Equations. Academic Press, New York (1977)
Stoer, J., Bulirsch, R.: Introduction to Numerical Analysis. Springer, New York (1993)
Jarausch, H., Mackens, W.: Computing solution branches by use of a condensed Newton-supported Picard iteration scheme. ZAMM Z. Angew. Math. Mech. 64, 282–284 (1981)
Simpson, R.: A method for the numerical determination of bifurcation states of nonlinear systems of equations. SIAM J. Numer. Anal. 12, 439–451 (1975)
Karkowski, J.: Numerical experiments with the Bratu equation in one, two and three dimensions. Comp. Appl. Math. 32, 231–244 (2013)
Shampine, L.F., Reichelt, M.W., Kierzenka, J.: Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. https://www.mathworks.com/help/matlab/ref/bvp4c.html
Mohsen, A., Sedeek, L.F., Mohamed, S.A.: New smoother to enhance multigrid-based methods for Bratu problem. Appl. Math. Comput. 204, 325–339 (2008)
Moore, G., Spence, A.: The calculation of turning points of nonlinear equations. SIAM J. Numer. Anal. 17(4), 567–576 (1980)
Acknowledgments
The authors would like to express their deep gratitude to the editor and anonymous referees for their careful reading and valuable suggestions to improve the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hajipour, M., Jajarmi, A. & Baleanu, D. On the accurate discretization of a highly nonlinear boundary value problem. Numer Algor 79, 679–695 (2018). https://doi.org/10.1007/s11075-017-0455-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-017-0455-1