A Crank-Nicolson-type compact difference method and its extrapolation for time fractional Cattaneo convection-diffusion equations with smooth solutions

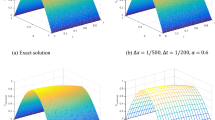
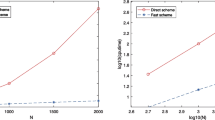
Abstract

A high-order Crank-Nicolson-type compact difference method is proposed for a class of time fractional Cattaneo convection-diffusion equations with smooth solutions. The convection coefficient of the equation may be spatially variable. A suitable transformation is adopted to transform the original equation into a reaction-diffusion equation, which is then discretized by a fourth-order compact difference approximation for the spatial derivative and by a second-order Crank-Nicolson-type difference approximation for the time first derivative and the Caputo time fractional derivative. The local truncation error and the solvability of the resulting scheme are discussed in detail. The (almost) unconditional stability of the method and its convergence of second order in time and fourth order in space are rigorously proved using a discrete energy analysis method. A Richardson extrapolation algorithm, including its rigorous convergence analysis, is presented. This extrapolation algorithm improves the temporal accuracy of the computed solution to the third order. An application of the proposed method to the non-smooth solution which has a weak singularity at the initial time is also discussed by introducing a correction term. Numerical results demonstrate the accuracy of the new method and the high efficiency of the Richardson extrapolation algorithm.

Appendices

Appendix A

A.1 Proof of Proposition 2.1

Proof

Since y(t) ∈ C^r[0,T], its extension y_ex(t) is r-times continuously differentiable at $t\in \mathbb {R} \setminus \{0\}$ and has one-sided derivatives of order up to r at t = 0. This implies y_ex(t) ∈ C^r[0,∞). Moreover, for each k = 0, 1,…,r, ${y}_{\text {ex}}^{(k)}(t)$ is absolutely integrable on $\mathbb {R}$ (define, e.g., ${y}_{\text {ex}}^{(k)}(0) = y^{(k)}(0)$) and thus its Fourier transformation ${\mathcal {F}} \left [{y}_{\text {ex}}^{(k)}\right ](\omega )$ is defined.

Assume, by contradiction, that there exists 0 ≤ r^′≤ r − 1 such that y^(k)(0) = 0 for k = 0, 1,…,r^′− 1 but $y^{(r^{\prime })}(0)\not = 0$. By integrating by parts,

$$\begin{array}{@{}rcl@{}} {\mathcal{F}} \left[{y}_{\text{ex}}^{(r^{\prime}+ 1)}\right] (\omega) &=& {{\int}_{0}^{\infty}} \mathrm{e}^{\mathrm{i}\omega t} {y}_{\text{ex}}^{(r^{\prime}+ 1)}(t) \mathrm{d}t = -y^{(r^{\prime})}(0) - \mathrm{i} \omega {\mathcal{F}} \left[{y}_{\text{ex}}^{(r^{\prime})}\right] (\omega)\\ &=& -y^{(r^{\prime})}(0) + (-\mathrm{i}\omega)^{2} {\mathcal{F}} \left[{y}_{\text{ex}}^{(r^{\prime}-1)}\right] (\omega)\\ &=& {\cdots} = -y^{(r^{\prime})}(0) + (-\mathrm{i}\omega)^{r^{\prime}+ 1} \hat{y}_{\text{ex}}(\omega). \end{array} $$

(A.1)

By the Riemann-Lebesgue lemma (see [55]), ${\lim _{|\omega |\rightarrow \infty }} {\mathcal {F}} \left [{y}_{\text {ex}}^{(r^{\prime }+ 1)}\right ] (\omega )= 0$. We therefore obtain from (A.1) that $\lim _{|\omega |\rightarrow \infty }(-\mathrm {i}\omega )^{r^{\prime }+ 1} \hat {y}_{\text {ex}}(\omega )= y^{(r^{\prime })}(0)\not = 0$. This implies

$$\begin{array}{@{}rcl@{}} \underset{|\omega|\rightarrow \infty}{\lim} |\omega|^{r^{\prime} + 1 - r_{0} - \beta} \left|\omega\right|^{r_{0}+\beta} \left|\hat{y}_{\text{ex}}(\omega)\right| = \underset{|\omega|\rightarrow \infty}{\lim} |\omega|^{r^{\prime}+ 1} \left|\hat{y}_{\text{ex}}(\omega)\right| = \left|y^{(r^{\prime})}(0)\right|\not= 0. \end{array} $$

Since r^′ + 1 − r₀ − β < 1, we get that the function $|\omega |^{r_{0}+\beta } |\hat {y}_{\text {ex}}(\omega )|$ is not integrable on $\mathbb {R}$. This contradicts $y_{\text {ex}}(t) \in \mathscr{C}^{r_{0}+\beta } (\mathbb {R})$. This proves that y^(k)(0) = 0 for k = 0, 1,…,r − 1. □

A.2 Proof of Proposition 4.1

Proof

For each k = 2, 3, 4, we define

$$ w_{k}(x,t) = \sigma \frac{\partial^{k + 1} u}{\partial t^{k-1} \partial x^{2}} (x,t) + q(x) \frac{\partial^{k-1} u}{\partial t^{k-1}}(x,t) - \frac{\partial^{k} u}{\partial t^{k}}(x,t) - \gamma {{~}_{~0}^{C} {\mathcal{D}}_{t}^{k-1+\alpha}} u(x,t). $$

(A.2)

Case 1: k = 2. Differentiating the governing equation in (??) with respect to t, we obtain

$$ \frac{\partial^{2} u}{\partial t^{2}}(x,t) = - \gamma \frac{\partial ({{}_{~0}^{C}{\mathcal{D}}_{t}^{\alpha}}u)}{\partial t} (x,t) + \sigma \frac{\partial^{3} u}{\partial t\partial x^{2}}(x,t) + q(x) \frac{\partial u}{\partial t} (x,t) + \frac{\partial g}{\partial t}(x,t), \,\,\,\,\, t\not= 0. $$

(A.3)

By integrating by parts and differentiating with respect to t,

$$\begin{array}{@{}rcl@{}} \frac{\partial ({{}_{~0}^{C}{\mathcal{D}}_{t}^{\alpha}}u)}{\partial t}(x,t) = \frac{\partial^{2} u}{\partial t^{2}}(x,0) \frac{1}{{\Gamma} (2-\alpha) t^{\alpha-1}} + {{}_{~0}^{C}{\mathcal{D}}_{t}^{1+\alpha}}u(x,t), \qquad t\not = 0. \end{array} $$

(A.4)

We thus have from (A.3) that

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2} u}{\partial t^{2}}(x,0) = \frac{{\Gamma} (2-\alpha)}{\gamma}w_{2}(x,t)t^{\alpha-1}+F_{2}(x,t), \qquad t\not= 0. \end{array} $$

(A.5)

The continuation property of w₂(x,t) and α ∈ (1, 2) imply ${\lim _{t\rightarrow 0}} w_{2}(x,t)t^{\alpha -1}= 0$. This proves that the limit ${\lim _{t\rightarrow 0}} F_{2}(x,t)$ exists and (??) holds true for k = 2.

Case 2: k = 3. Differentiating the (A.3) and (A.4) with respect to t gives

$$\begin{array}{@{}rcl@{}} \frac{\partial^{3} u}{\partial t^{3}}(x,t) &=& -\gamma \frac{\partial^{2} ({{}_{0}^{\mathcal{C}}{\mathcal{D}}_{t}^{\alpha}u})}{\partial t^{2}}(x,t)+\sigma \frac{\partial^{4} u}{\partial t^{2} \partial x^{2}}(x,t) + q(x) \frac{\partial^{2} u}{\partial t^{2}}(x,t)\\ &&+ \frac{\partial^{2} g}{\partial t^{2}}(x,t), \qquad t\not= 0, \end{array} $$

(A.6)

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2} ({{}_{~0}^{C}{\mathcal{D}}_{t}^{\alpha}}u)}{\partial t^{2}}(x,t) &=& \frac{1}{{\Gamma} (2-\alpha) t^{\alpha-1}} \left( \frac{\partial^{2} u}{\partial t^{2}}(x,0) \frac{1 - \alpha}{t} + \frac{\partial^{3} u}{\partial t^{3}}(x,0)\right)\\ &&+ {{}_{~0}^{C}{\mathcal{D}}_{t}^{2+\alpha}} u(x,t), \qquad t\not= 0. \end{array} $$

(A.7)

This shows

$$\begin{array}{@{}rcl@{}} \frac{\partial^{3} u}{\partial t^{3}}(x,0) = \frac{{\Gamma} (2-\alpha)}{\gamma} w_{3}(x,t)t^{\alpha-1} + F_{3}(x,t), \qquad t\not= 0. \end{array} $$

(A.8)

Letting t → 0 in (A.8), we get (??) for k = 3.

Case 3: k = 4. Differentiating the (A.6) and (A.7) with respect to t and solving for $\frac {\partial ^{4} u}{\partial t^{4}}(x,0)$, we obtain

$$\begin{array}{@{}rcl@{}} \frac{\partial^{4} u}{\partial t^{4}}(x,0) = \frac{{\Gamma} (2-\alpha)}{\gamma}w_{4}(x,t)t^{\alpha-1}+F_{4}(x,t), \qquad t\not= 0. \end{array} $$

(A.9)

Then, (??) for k = 4 follows by letting t → 0 in the above equality. □