Skip to main content
SpringerLink
Log in

A shrinking projection method for solving the split common null point problem in Banach spaces

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

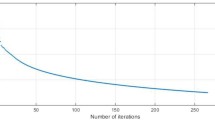
In this paper, in order to solve the split common null point problem, we investigate a new explicit iteration method, base on the shrinking projection method and ε-enlargement of a maximal monotone operator. We also give some applications of our main results for the problem of split minimum point, multiple-sets split feasibility, and split variational inequality. Two numerical examples also are given to illustrate the effectiveness of the proposed algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Agarwal, R.P., O’Regan, D., Sahu, D.R.: Fixed point theory for Lipschitzian-type mappings with applications. Springer (2009)

  2. Alber, Y.I.: Metric and generalized projections in Banach spaces: properties and applications. In: Kartsatos, A.G. (ed.) Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, pp. 15–50 (1996)

  3. Alber, Y.I., Reich, S.: An iterative method for solving a class of nonlinear operator in Banach spaces. Panamer. Math. J. 4, 39–54 (1994)

    MathSciNet  MATH  Google Scholar 

  4. Byrne, C.: Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl. 18(2), 441–453 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  5. Byrne, C.: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 18, 103–120 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  6. Byrne, C., Censor, Y., Gibali, A., Reich, S.: The split common null point problem. J. Nonlinear Convex Anal. 13, 759–775 (2012)

    MathSciNet  MATH  Google Scholar 

  7. Browder, F.E.: Nonlinear maximal monotone operators in Banach spaces. Math. Ann. 175, 89–113 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  8. Burachik, R.S., Iusem, A.N., Svaiter, B.F.: Enlargement of monotone operators with applications to variational inequalities. Set-Valued Anal. 5, 159–180 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  9. Burachik, R.S., Svaiter, B.F.: ε-Enlargements of maximal monotone operators in Banach spaces. Set-Valued Anal. 7, 117–132 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  10. Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms. 8(2-4), 221–239 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  11. Censor, Y., Elfving, T., Kopf, N., Bortfeld, T.: The multiple-sets split feasibility problem and its application. Inverse Probl. 21, 2071–2084 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  12. Censor, Y., Segal, A.: The split common fixed point problem for directed operators. J. Convex Anal. 16, 587–600 (2009)

    MathSciNet  MATH  Google Scholar 

  13. Censor, Y., Gibali, A., Reich, R.: Algorithms for the split variational inequality problems. Numer. Algo. 59, 301–323 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. Dadashi, V.: Shrinking projection algorithms for the split common null point problem. Bull. Aust. Math. Soc. 99(2), 299–306 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  15. Goebel, K., Kirk, W.A.: Topics in metric fixed point theory. Cambridge Stud. Adv Math., vol. 28. Cambridge Univ. Press, Cambridge (1990)

    Book  Google Scholar 

  16. Kamimura, S., Takahashi, W.: Strong convergence of a proximal-type algorithm in a Banach space. SIAM J. Optim. 13, 938–945 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  17. Masad, E., Reich, S.: A note on the multiple-set split convex feasibility problem in Hilbert space. J. Nonlinear Convex Anal. 8, 367–371 (2007)

    MathSciNet  MATH  Google Scholar 

  18. Mosco, U.: Convergence of convex sets and of solutions of variational inequalities. Adv. Math. 3, 510–585 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  19. Moudafi, A.: The split common fixed point problem for demicontractive mappings. Inverse Probl. 26(5), 055007 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  20. Reich, S.: Book review: Geometry of Banach spaces, duality mappings and nonlinear problems. Bull. Amer. Math. Soc. 26, 367–370 (1992)

    Article  MathSciNet  Google Scholar 

  21. Rockafellar, R.T.: On the maximal monotonicity of subdifferential mappings. Pacific J. Math. 33(1), 209–216 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  22. Rockafellar, R.T.: On the maximality of sums of nonlinear monotone operators. Trans. Amer. Math. Soc. 149, 75–88 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  23. Takahashi, W.: Convex analysis and approximation of fixed points. Yokohama Publishers Yokohama (2000)

  24. Takahashi, W.: The split feasibility problem in Banach spaces. J. Nonlinear Convex Anal. 15, 1349–1355 (2014)

    MathSciNet  MATH  Google Scholar 

  25. Takahashi, W.: The split feasibility problem and the shrinking projection method in Banach spaces. J. Nonlinear Convex Anal. 16(7), 1449–1459 (2015)

    MathSciNet  MATH  Google Scholar 

  26. Takahashi, S., Takahashi, W.: The split common null point problem and the shrinking projection method in Banach spaces. Optimization 65(2), 281–287 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  27. Takahashi, W.: The split common null point problem in Banach spaces. Arch. Math. 104, 357–365 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  28. Tsukada, M.: Convergence of best approximations in a smooth Banach space. J. Approx. Theory. 40, 301–309 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  29. Xu, H.K.: A variable Krasnosel’skii-Mann algorithm and the multiple-set split feasibility problem. Inverse Probl. 22, 2021–2034 (2006)

    Article  MATH  Google Scholar 

  30. Xu, H.K.: Iterative methods for the split feasibility problem in infinite dimensional Hilbert spaces. Inverse Probl. 105018, 26 (2010)

    MathSciNet  Google Scholar 

  31. Yang, Q.: The relaxed CQ algorithm for solving the problem split feasibility problem. Inverse Probl. 20, 1261–1266 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang, F., Xu, H.K.: Cyclic algorithms for split feasibility problems in Hilbert spaces. Nonlinear Anal. 74, 4105–4111 (2011)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Thai Nguyen University of Science, Thai Nguyen, Vietnam

    Truong Minh Tuyen & Nguyen Song Ha

  2. School of Applied Mathematics and Informatics, Hanoi University of Science and Technology, Hanoi, Vietnam

    Nguyen Thi Thu Thuy

Authors
  1. Truong Minh Tuyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nguyen Song Ha
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nguyen Thi Thu Thuy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Truong Minh Tuyen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tuyen, T.M., Ha, N.S. & Thuy, N.T.T. A shrinking projection method for solving the split common null point problem in Banach spaces. Numer Algor 81, 813–832 (2019). https://doi.org/10.1007/s11075-018-0572-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-018-0572-5

Keywords

Mathematics Subject Classification (2010)

Search

Navigation