Abstract
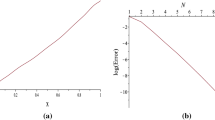
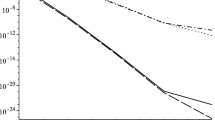
This paper presents a computational method based on least squares method and block pulse functions for solving Itô-Volterra integral equation. The Itô-Volterra integral equation is converted to a linear system of algebraic equations by the least squares method on the block pulse functions. The error analysis of the proposed method is investigated by providing theorems. Numerical examples show the accuracy and reliability of the presented method. The numerical results confirm that the presented method is more accurate than the block pulse functions operational matrix method.



Similar content being viewed by others
References
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, vol. 408. Springer, Berlin (2011)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Choe, G.H.: Stochastic Analysis for Finance with Simulations. Springer, Berlin (2016)
Cioica, P.A., Dahlke, S.: Patial besov regularity for semilinear stochastic partial differential equations on bounded lipschitz domains. S, Acta Math. Int. J Comput. Math. 18(89), 2443–2459 (2012)
Cortes, J.C., Jodar, L., Villafuerte, L.: Mean square numerical solution of random differential equations: facts and possibilities. Comput. Math. Appl. 53, 1098–1106 (2007)
Cortes, J.C., Jodar, L., Villafuerte, L.: Numerical solution of random differential equations: a mean square approach. Math. Comput. Model. 45, 757–765 (2007)
Ehler, M.: Shrinkage rules for variational minimization problems and applications to analytical ultracentrifugation. J. Inverse Ill-Posed Probl. 19(4-5), 593–614 (2011)
Elworthy, K.D., Truman, A., Zhao, H.Z., Gaines, J.G.: Approximate traveling waves for generalized kpp equations and classical mechanics. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci., 446
Ernst, P.A., Soleymani, F.: A legendre-based computational method for solving a class of itô, stochastic delay differential equations. Numer Algor. 80, 1267–1282 (2019)
Heydari, M.H., Hooshmandasl, M.R., Cattani, C., Ghaini, F.M.M.: An efficient computational method for solving nonlinear stochastic itô integral equations Application for stochastic problems in physics. J. Comput. Phys. 283, 148–168 (2015)
Heydari, M.H., Hooshmandasl, M.R., Maalek, F.M., Cattani, C.: A computational method for solving stochastic itô,–volterra integral equations based on stochastic operational matrix for generalized hat basis functions. J Comput. Phys. 270, 402–415 (2014)
Higham, D.J.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43(3), 525–546 (2001)
Jankovic, S., Ilic, D.: One linear analytic approximation for stochastic integro-differential equations. Acta Math. Sci. 30, 1073–1085 (2010)
Jiang, Z.H., Schaufelberger, W.: Block Pulse Functions and Their Applications in Control Systems. Springer, Berlin (1992)
Klebaner, F.C.: Introduction to Stochastic Calculus with Applications. Imperial College Press (1998)
Kloeden, P.E., Platen, E.: Numerical Solution of Stochastic Differential Equations Applications of Mathematics. Springer, Berlin (1999)
Maleknejad, K., Khodabin, M., Rostami, M.: Numerical solution of stochastic volterra integral equations by a stochastic operational matrix based on block pulse functions. Math Comput. Model. 55, 791–800 (2012)
Miller, R.K.: On a system of integro-differential equations occuring in reactor dynamic. Math. Comp. 14, 446–452 (1996)
Mirzaee, F., Samadyar, N.: Application of hat basis functions for solving two-dimensional stochastic fractional integral equations. Comput. Appl Math. 37, 4899–4916 (2018)
Mirzaee, F., Samadyar, N.: On the numerical solution of stochastic quadratic integral equations via operational matrix method. Math. Meth. Appl. Sci. 41, 4465–4479 (2018)
Mohammadi, F.: A wavelet-based computational method for solving stochastic itô-volterra integral equations. J. Comput. Phys. 289, 254–265 (2015)
Mohammadi, F.: Second kind chebyshev wavelet galerkin method for stochastic itô-volterra integral equations. Mediterr. J. Math. 13, 2613–2631 (2016)
Mohammadi, F.: Numerical treatment of nonlinear stochastic itô–volterra integral equations by piecewise spectral-collocation method. J. Comput. Nonlinear Dyn. 14(3), 031007 (2019)
Murge, M.G., Pachpatte, B.G.: Successiveapproximations for solutions of second order stochastic integro-differential equations of ito type. Indian J Pure Appl. Math. 21(3), 260–274 (1990)
Oksendal, B.: Stochastic differential equations: an introduction with applications. Springer, Berlin (1998)
Platen, E., Bruti-Liberati, N.: Numerical Solution of Stochastic Differential Equations with Jumps in Finance. Springer, Berlin (2010)
Rivlin, T.J.: An Introduction to the Approximation of Functions. Dover Publications, New York (1981)
Saffarzadeh, M., Loghmani, G.B., Heydari, M.: An iterative technique for the numerical solution of nonlinear stochastic itô, –volterra integral equations. J. Comput. Appl Math. 333, 74–86 (2018)
Acknowledgments
We would like to thank Professor Mokhtar Abbasi and anonymous referees for their valuable comments and suggestions, which helped us to considerably improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ahmadinia, M., A., H.A. & Heydari, M. Numerical solution of Itô-Volterra integral equation by least squares method. Numer Algor 84, 591–602 (2020). https://doi.org/10.1007/s11075-019-00770-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-019-00770-2