Skip to main content
Springer Nature Link
Log in

Numerical approximation of the fractional Cahn-Hilliard equation by operator splitting method

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

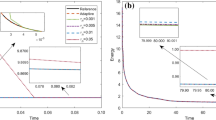
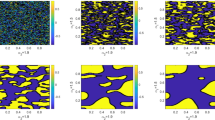
In this paper, we consider a fast explicit operator splitting method for a fractional Cahn-Hilliard equation with spatial derivative \((-{\varDelta })^{\frac {\alpha }{2}}\)(α ∈ (1,2]), where the choice α = 2 corresponds to the classical Cahn-Hilliard equation. The original problem is split into linear and nonlinear subproblems. For the linear part, the pseudo-spectral method is adopted, and thus an ordinary differential equation is obtained. For the nonlinear part, a second-order SSP-RK method together with the pseudo-spectral method is used. The stability and convergence of the proposed method in L2-norm are studied. We also carry out a comparative study of two classical definitions for fractional Laplacian \((-{\varDelta })^{\frac {\alpha }{2}}\), and numerical results obtained using computational simulation of the fractional Cahn-Hilliard equation for a variety of choices of fractional order α are presented. It is observed that the fractional order α controls the sharpness of the interface, which is typically diffusive in integer-order phase-field models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Cahn, J., Hilliard, J.: Free energy of a nonuniform system. I: Interfacial energy. J. Chem. Phys. 28, 258 (1958)

    MATH  Google Scholar 

  2. Cahn, J., Hilliard, J.: Free energy of a nonuniform system. II: Thermodynamic basis. J. Chem. Phys. 30, 1121–1135 (1959)

    Google Scholar 

  3. Chan, P.K., Rey, A.D.: A numerical method for the nonlinear Cahn-Hilliard equation with nonperiodic boundary conditions. Comp. Mater. Sci. 3, 377–392 (1995)

    Google Scholar 

  4. Dolcetta, I.C., Vita, S.F., March, R.: Area-preserving curve-shortening flows: from phase separation to image processing. Interface Free Bound. 4, 325–343 (2002)

    MATH  MathSciNet  Google Scholar 

  5. Sun, Z.Z.: A second-order accurate linearized difference scheme for the two-dimensional Cahn-Hilliard equation. Math. Comput. 64, 1463–1471 (1995)

    MATH  MathSciNet  Google Scholar 

  6. Wise, S.M.: Unconditionally stable finite difference, nonlinear multigrid simulation of the Cahn-Hilliard-Hele-Shaw system of equations. J. Sci. Comput. 44, 38–68 (2010)

    MATH  MathSciNet  Google Scholar 

  7. Li, Y.B., Lee, H.G., Xia, B.H., Kim, J.: A compact fourth-order finite difference scheme for the three-dimensional Cahn-Hilliard equation. Comput. Phys. Commun. 200, 108–116 (2016)

    MATH  MathSciNet  Google Scholar 

  8. Elliott, C.M., French, D.A.: A nonconforming finite-element method for the two-dimensional Cahn-Hilliard equation. SIAM J. Numer. Anal. 26, 884–903 (1989)

    MATH  MathSciNet  Google Scholar 

  9. Elliott, C.M., Ranner, T.: Evolving surface finite element method for the Cahn-Hilliard equation. Numer. Math. 129, 483–534 (2015)

    MATH  MathSciNet  Google Scholar 

  10. Yan, Y., Chen, W.B., Wang, C., Wise, S.M.: A second-order energy stable BDF numerical scheme for the Cahn-Hilliard equation. Commun. Comput. Phys. 23, 572–602 (2018)

    MathSciNet  Google Scholar 

  11. Shen, J., Yang, X.F.: Numerical approximations of Allen-Cahn and Cahn-Hilliard equations. Discrete Contin. Dyn. Syst. 28, 1669–1691 (2010)

    MATH  MathSciNet  Google Scholar 

  12. Cheng, K.L., Wang, C., Wise, S.M., Yue, X.Y., second-order, A: weakly energy-stable pseudo-spectral scheme for the Cahn-Hilliard equation and its solution by the homogeneous linear iteration method. J. Sci. Comput. 69, 1083–1114 (2016)

    MATH  MathSciNet  Google Scholar 

  13. Li, D., Qiao, Z.H.: On second order semi-implicit Fourier spectral methods for 2D Cahn-Hilliard equations. J. Sci. Comput. 70, 301–341 (2017)

    MATH  MathSciNet  Google Scholar 

  14. Felgueroso, L.C., Peraire, J.: A time-adaptive finite volume method for the Cahn-Hilliard and Kuramoto-Sivashinsky equations. J. Comput. Phys. 227, 9985–10017 (2008)

    MATH  MathSciNet  Google Scholar 

  15. Herrmann, R.: Fractional Calculus: An Introduction for Physicists, 2nd edn. World Scientific, River Edge (2014)

    MATH  Google Scholar 

  16. Atanackovic, T.M., Pilipovic, S., Stankovic, B., Zorica, D.: Fractional Calculus with Applications in Mechanics: Wave Propagation. Impact and Variational Principles. ISTE Ltd, London (2014)

    MATH  Google Scholar 

  17. Bosch, J., Stoll, M.: A fractional inpainting model based on the vector-valued Cahn-Hilliard equation. SIAM J. Imaging Sci. 8, 2352–2382 (2015)

    MATH  MathSciNet  Google Scholar 

  18. Akag, G., Schimperna, G., Segatti, A.: Fractional Cahn-Hilliard, Allen-Cahn and porous medium equations. J. Differ. Equations 261, 2935–2985 (2016)

    MATH  MathSciNet  Google Scholar 

  19. Hu, Y., He, J.H.: On fractal space-time and fractional calculus. Therm. Sci. 20(3), 773–777 (2016)

    MathSciNet  Google Scholar 

  20. Ainsworth, M., Mao, Z.P.: Well-posedness of the Cahn-Hilliard equation with fractional free energy and its Fourier Galerkin approximation. Chaos Soliton. Fract. 102, 264–273 (2017)

    MATH  MathSciNet  Google Scholar 

  21. Yang, Q., Turner, I., Liu, F., Ili’c, M.: Novel numerical methods for solving the time-space fractional diffusion equation in 2D. SIAM J. Sci. Comp. 33, 1159–1180 (2011)

    Google Scholar 

  22. Orovio, A., Kay, D., Burrage, K.: Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 54, 937–954 (2014)

    MATH  MathSciNet  Google Scholar 

  23. Zhai, S.Y., Weng, Z.F., Feng, X.L.: Fast explicit operator splitting method and time-step adaptivity for fractional non-local Allen-Cahn model. Appl. Math Model. 40, 1315–1324 (2016)

    MATH  MathSciNet  Google Scholar 

  24. Weng, Z.F., Zhai, S.Y., Feng, X.L.: A Fourier spectral method for fractional-in-space Cahn-Hilliard equation. Appl. Math. Model. 42, 462–477 (2017)

    MATH  MathSciNet  Google Scholar 

  25. Gottlieb, S., Shu, C.: Total variation diminishing Runge-Kutta schemes. Math. Comput. 67, 73–85 (1998)

    MATH  MathSciNet  Google Scholar 

  26. Strang, G.: On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 5, 506–517 (1968)

    MATH  MathSciNet  Google Scholar 

  27. Gatto, P., Hesthaven, J.S.: Numerical approximation of the fractional Laplacian via hp-finite elements, with an application to image denoising authors. J. Sci. Comput. 65, 249–270 (2015)

    MATH  MathSciNet  Google Scholar 

  28. Song, F.Y., Xu, C.J., Karniadakis, G.E.: Computing fractional Laplacians on complex-geometry domains: algorithms and simulations. SIAM J. Sci. Comput. 39, A1320–A1344 (2017)

    MATH  MathSciNet  Google Scholar 

  29. Shen, S.J., Liu, F.W., Anh, V.: Numerical approximations and solution techniques for the space-time Riesz-Caputo fractional advection-diffusion equation. Numer Algorithms 56, 383–403 (2011)

    MATH  MathSciNet  Google Scholar 

  30. Zhao, X., Sun, Z.Z., Hao, Z.P.: A foyrth-order compact ADI scheme for two-dimensional nonlinear space fractional schrödinger equation. SIAM J. Sci. Comput. 36, A2865–A2886 (2014)

    MATH  Google Scholar 

  31. Ding, H.F., Li, C.P.: High-order numerical algorithms for Riesz derivatives via constructing new generating functions. J. Sci. Comput. 71, 759–784 (2017)

    MATH  MathSciNet  Google Scholar 

  32. Shen, J., Tang, T., Wang, L.L.: Spectral Methods Algorithms: Analyses and Applications, 1st edn. Springer, Berlin (2010)

    Google Scholar 

  33. Ainsworth, M., Mao, Z.P.: Analysis and approximation of a fractional Cahn-Hilliard equation. SIAM J. Numer. Anal. 55, 1689–1718 (2017)

    MATH  MathSciNet  Google Scholar 

  34. Li, X., Qiao, Z.H., Zhang, H.: Convergence of a fast explicit operator splitting method for the epitaxial growth model with slope selection. SIAM J. Numer. Anal. 55, 265–285 (2017)

    MATH  MathSciNet  Google Scholar 

  35. Mishra, S., Sv̈ard, M.: On stability of numerical schemes via frozen coefficients and the magnetic induction equations. BIT Numer. Math. 50, 85–108 (2010)

    MathSciNet  Google Scholar 

  36. Orovio, A.B., Kay, D., Burrage, K.: Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 54, 937–954 (2014)

    MATH  MathSciNet  Google Scholar 

  37. Chandru, M., Das, P., Ramos, H.: Numerical treatment of two-parameter singularly perturbed parabolic convection diffusion problems with non-smooth data. Math. Methods Appl. Sci. 41, 5359–5387 (2018)

    MATH  MathSciNet  Google Scholar 

  38. Chandru, M., Prabha, T., Das, P., Shanthi, V.: A numerical method for solving boundary and interior layers dominated parabolic problems with discontinuous convection coefficient and source terms. Differ. Equ. Dyn. Syst. 27, 97–112 (2019)

    MATH  MathSciNet  Google Scholar 

  39. Das, P., Mehrmann, V.: Numerical solution of singularly perturbed convection-diffusion-reaction problems with two small parameters. BIT Numer. Math. 56, 51–76 (2016)

    MATH  MathSciNet  Google Scholar 

  40. Das, P.: A higher order difference method for singularly perturbed parabolic partial differential equations. J. Differ. Equ. Appl. 24, 452–477 (2018)

    MATH  MathSciNet  Google Scholar 

  41. Das, P.: An a posteriori based convergence analysis for a nonlinear singularly perturbed system of delay differential equations on an adaptive mesh. Numer. Algorithms, https://doi.org/10.1007/s11075-018-0557-4 (2018)

  42. Das, P., Vigo-Aguiar, J.: Parameter uniform optimal order numerical approximation of a class of singularly perturbed system of reaction diffusion problems involving a small perturbation parameter. J. Comput. Appl. Math. 354, 533–544 (2019)

    MATH  MathSciNet  Google Scholar 

  43. Das, P., Natesan, S.: Optimal error estimate using mesh equidistribution technique for singularly perturbed system of reaction-diffusion boundary-value problems. Appl. Math. Comput. 249, 265–277 (2014)

    MATH  MathSciNet  Google Scholar 

  44. Das, P.: Comparison of a priori and a posteriori meshes for singularly perturbed nonlinear parameterized problems. J. Comput. Appl. Math. 290, 16–25 (2015)

    MATH  MathSciNet  Google Scholar 

  45. Das, P., Natesan, S.: Adaptive mesh generation for singularly perturbed fourth-order ordinary differential equations. Int. J. Comput. Math. 92, 562–578 (2015)

    MATH  MathSciNet  Google Scholar 

  46. Das, P., Natesan, S.: Richardson extrapolation method for singularly perturbed convection-diffusion problems on adaptively generated mesh. CMES Comput. Model. Eng. Sci. 90, 463–485 (2013)

    MATH  MathSciNet  Google Scholar 

  47. Das, P., Natesan, S.: Higher order parameter uniform convergent schemes for Robin type reaction diffusion problems using adaptively generated grid. Int. J. Comput. Meth. 9, 1250052 (2012)

    MATH  MathSciNet  Google Scholar 

  48. Wodo, O., Ganapathysubramanian, B.: Computationally efficient solution to the Cahn-Hilliard equation: Adaptive implicit time schemes, mesh sensitivity analysis and the 3D isoperimetric problem. J. Comput. Phys. 230, 6037–6060 (2011)

    MATH  MathSciNet  Google Scholar 

  49. Zhang, Z.R., Ma, Y., Qiao, Z.H.: An adaptive time-stepping strategy for solving the phase field crystal model. J. Comput. Phys. 249, 204–215 (2013)

    MATH  MathSciNet  Google Scholar 

  50. Lubich, C.: On splitting methods for Schrödinger-Poisson and cubic nonlinear Schrödinger equations. Math. Comp. 77, 2141–2153 (2008)

    MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors thank the editor and referees for their constructive comments and useful suggestions which improved greatly the quality of our paper.

Funding

This work is in part supported by the NSF of China (nos. 11701196 and 11701197), the Promotion Program for Young and Middle-Aged Teacher in Science and Technology Research of Huaqiao University (no. ZQN-YX502), and the Fundamental Research Funds for the Central Universities (No. ZQN-702).

Author information

Authors and Affiliations

  1. Fujian Province University Key Laboratory of Computation Science, Huaqiao University, Quanzhou, 362021, People’s Republic of China

    Shuying Zhai, Longyuan Wu, Jingying Wang & Zhifeng Weng

Authors
  1. Shuying Zhai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Longyuan Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jingying Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Zhifeng Weng
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhifeng Weng.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhai, S., Wu, L., Wang, J. et al. Numerical approximation of the fractional Cahn-Hilliard equation by operator splitting method. Numer Algor 84, 1155–1178 (2020). https://doi.org/10.1007/s11075-019-00795-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-019-00795-7

Keywords

Mathematics Subject Classification (2010)