Skip to main content
Springer Nature Link
Log in

On the numerical structure preservation of nonlinear damped stochastic oscillators

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

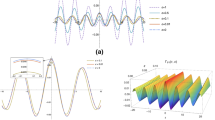
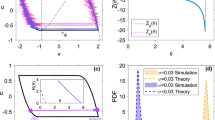
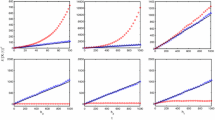
The paper is focused on analyzing the conservation issues of stochastic 𝜃-methods when applied to nonlinear damped stochastic oscillators. In particular, we are interested in reproducing the long-term properties of the continuous problem over its discretization through stochastic 𝜃-methods, by preserving the correlation matrix. This evidence is equivalent to accurately maintaining the stationary density of the position and the velocity of a particle driven by a nonlinear deterministic forcing term and an additive noise as a stochastic forcing term. The provided analysis relies on a linearization of the nonlinear problem, whose effectiveness is proved theoretically and numerically confirmed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Anton, R., Cohen, D.: Exponential integrators for stochastic schrödinger equations driven by Ito noise. J. Comput. Math. 36(2), 276–309 (2019)

    MATH  Google Scholar 

  2. Buckwar, E., D’Ambrosio, R.: Exponential mean-square stability properties of stochastic multistep methods, submitted

  3. Buckwar, E., Sickenberger, T.: A comparative linear mean-square stability analysis of Maruyama- and Milstein-type methods. Math. Comput. Simul. 81, 1110–1127 (2011)

    Article  MathSciNet  Google Scholar 

  4. Bryden, A., Higham, D. J.: On the boundedness of asymptotic stability regions for the stochastic theta method. BIT 43, 1–6 (2003)

    Article  MathSciNet  Google Scholar 

  5. Burrage, P. M., Burrage, K.: Structure-preserving Runge-Kutta methods for stochastic Hamiltonian equations with additive noise. Numer. Algor. 65, 519–532 (2012)

    Article  MathSciNet  Google Scholar 

  6. Burrage, P. M., Burrage, K.: Low rank Runge-Kutta methods, symplecticity and stochastic Hamiltonian problems with additive noise. J. Comput. Appl. Math. 236, 3920–3930 (2014)

    Article  MathSciNet  Google Scholar 

  7. Burrage, K., Lenane, I., Lythe, G.: Numerical methods for second-order stochastic differential equations. SIAM. J. Sci. Comput. 29(1), 245–264 (2007)

    MathSciNet  MATH  Google Scholar 

  8. Burrage, K., Lythe, G.: Accurate stationary densities with partitioned numerical methods for stochastic differential equations. SIAM. J. Numer. Anal. 47, 1601–1618 (2009)

    Article  MathSciNet  Google Scholar 

  9. Burrage, K., Lythe, G.: Accurate stationary densities with partitioned numerical methods for stochastic partial differential equations. Stochastic Partial Differential Equations: Analysis and Computations. 2(2), 262–280 (2014)

    Article  MathSciNet  Google Scholar 

  10. Chen, C., Cohen, D., D’Ambrosio, R., Lang, A.: Drift-preserving numerical integrators for stochastic Hamiltonian systems. Adv. Comput. Math. 46(2), 27 (2020)

    Article  MathSciNet  Google Scholar 

  11. Citro, V., D’Ambrosio, R.: Long-term analysis of stochastic 𝜃-methods for damped stochastic oscillators, Appl. Numer. Math. 18–26. https://doi.org/10.1016/j.apnum.2019.08.011 (2019)

  12. Citro, V., D’Ambrosio, R., Di Giovacchino, S.: A-stability preserving perturbation of Runge–Kutta methods for stochastic differential equations, Appl. Math. Lett. 102, 106098 (2020)

    MathSciNet  MATH  Google Scholar 

  13. Cohen, D., Gauckler, L., Hairer, E., Lubich, C.: Long-term analysis of numerical integrators for oscillatory Hamiltonian systems under minimal non-resonance conditions, BIT. Numer. Math. 55(3), 705–732 (2015)

    Article  Google Scholar 

  14. Conte, D., D’Ambrosio, R., Paternoster, B.: On the stability of 𝜃-methods for stochastic Volterra integral equations. Discret. Cont. Dyn. Syst. B 23, 2695–2708 (2018)

    MathSciNet  MATH  Google Scholar 

  15. D’Ambrosio, D., Moccaldi, M., Paternoster, B.: Numerical preservation of long-term dynamics by stochastic two-step methods. Discrete and Continuous Dynamical Systems Series B. 23(7), 2763–2773 (2018)

    Article  MathSciNet  Google Scholar 

  16. D’Ambrosio, R., Di Giovacchino, S.: Mean-square contractivity of stochastic 𝜃-methods, submitted.

  17. Gardiner, C. W.: Handbook of Stochastic Methods for Physics, Chemistry, and the Natural Sciences, 3rd ed. Springer-Verlag, Berlin (2004)

    Book  Google Scholar 

  18. Higham, D. J.: Mean-square asymptotic stability of the stochastic theta method. SIAM J. Numer. Anal. 38, 753–769 (2000)

    Article  MathSciNet  Google Scholar 

  19. Schurz, H.: The invariance of asymptotic laws of linear stochastic systems under discretization. Z. Angew. Math. Mech. 6, 375–382 (1999)

    Article  MathSciNet  Google Scholar 

  20. Strömmen Melbö, A. H., Higham, D. J.: Numerical simulation of a linear stochastic oscillator with additive noise. Appl. Numer. Math. 51, 89–99 (2004)

    Article  MathSciNet  Google Scholar 

  21. Vilmart, G.: Weak second order multirevolution composition methods for highly oscillatory stochastic differential equations with additive or multiplicative noise. SIAM J. Sci. Comput. 36(4), A1770–A1796 (2014)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors thank the anonymous referee, for valuable remarks, in particular, for suggesting further comparisons in Section 9. This work is supported by the GNCS-INDAM project and by the PRIN2017-MIUR project. The authors are member of the INdAM Research group GNCS.

Author information

Authors and Affiliations

  1. Department of Information Engineering and Computer Science and Mathematics, University of L’Aquila Via Vetoio, Loc. Coppito, 67100, L’Aquila, Italy

    Raffaele D’Ambrosio & Carmela Scalone

Authors
  1. Raffaele D’Ambrosio
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Carmela Scalone
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Raffaele D’Ambrosio.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

D’Ambrosio, R., Scalone, C. On the numerical structure preservation of nonlinear damped stochastic oscillators. Numer Algor 86, 933–952 (2021). https://doi.org/10.1007/s11075-020-00918-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-020-00918-5

Keywords

Mathematics Subject Classification (2010)