A class of new Magnus-type methods for semi-linear non-commutative Itô stochastic differential equations

Abstract

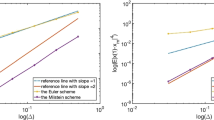
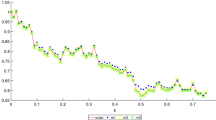
In this paper, a class of new Magnus-type methods is proposed for non-commutative Itô stochastic differential equations (SDEs) with semi-linear drift term and semi-linear diffusion terms, based on Magnus expansion for non-commutative linear SDEs. We construct a Magnus-type Euler method, a Magnus-type Milstein method and a Magnus-type Derivative-free method, and give the mean-square convergence analysis of these methods. Numerical tests are carried out to present the efficiency of the proposed methods compared with the corresponding underlying methods and the specific performance of the simulation Itô integral algorithms is investigated.

Appendix

1.1 A.1 The expansion of iterated Itô stochastic integrals based on the generalized multiple Fourier series

Let $\left \{\phi _{j}(x)\right \}_{j=0}^{\infty }$ be an orthonormal basis of the space $L_{2}\left (\left [t_{n}, t_{n+1}\right ]\right ).$ If the trigonometric series

$$ \phi_{j}(s)=\frac{1}{\sqrt{h}}\left\{\begin{array}{cc} 1, & j=0, \\ \sqrt{2} \sin \frac{2 \pi r\left( s-t_{n}\right)}{h}, & j=2 r-1, \\ \sqrt{2} \cos \frac{2 \pi r\left( s-t_{n}\right)}{h}, & j=2 r, \end{array}\right. $$

where r = 1, 2,…, are selected as an orthonormal basis, for the iterated Itô integral (7), using the expansion theorem in [20], the following representations are obtained,

$$ \begin{aligned} I_{ij}(t_{n}, t_{n}+h)=&\frac{1}{2}h\left[\zeta_{0}^{\left( j\right)} \zeta_{0}^{\left( i\right)}+\frac{1}{\pi} \sum\limits_{r=1}^{\infty} \frac{1}{r}\left\{\zeta_{2 r}^{\left( j\right)} \zeta_{2 r-1}^{\left( i\right)}-\zeta_{2 r-1}^{\left( j\right)} \zeta_{2 r}^{\left( i\right)}\right.\right.\\ &+\left.\left.\sqrt{2}\left( \zeta_{2 r-1}^{\left( j\right)} \zeta_{0}^{\left( i\right)}-\zeta_{0}^{\left( j\right)} \zeta_{2 r-1}^{\left( i\right)}\right)\right\}\right],~i\neq j, \end{aligned} $$

(A.1)

where $\zeta _{0}^{(i)} \underset {=}{\text { def }} W_{i}(h)/\sqrt {h}$ and $\zeta _{j}^{(i)} \underset {=}{\text { def }} {{\int \limits }_{t}^{T}} \phi _{j}(s) d W_{i}(s)$, i = 1,…,m. The expansion (A.1) coincides with Kloeden, Platen and Wright’s (1992) algorithm [23] based on Kahunen–Loève expansion and it converges to the iterated Itô integral (7) in the mean-square sense.

If orthonormal Legendre polynomials are selected as an orthonormal basis,

$$ \left\{\phi_{j}(s)\right\}_{j=0}^{\infty}, \phi_{j}(s)=\sqrt{\frac{2 j+1}{h}} P_{j}\left( \left( s-\frac{h}{2}\right) \frac{2}{h}\right) $$

the expansion is

$$ \begin{aligned} I_{ij}(t_{n}, t_{n}+h)=\frac{h}{2}\left[\zeta_{0}^{\left( i\right)} \zeta_{0}^{\left( j\right)}+\sum\limits_{r=1}^{\infty} \frac{1}{\sqrt{4 r^{2}-1}}\left\{\zeta_{r-1}^{\left( i\right)} \zeta_{r}^{\left( j\right)}-\zeta_{r}^{\left( i\right)} \zeta_{r-1}^{\left( j\right)}\right\}\right]. \end{aligned} $$

(A.2)

As the expansions (A.1) and (A.2) are infinite series, we need to truncate them for practical simulation. During the implementation of the Milstein and MM methods, the mean-square error of the approximated iterated integrals should not be larger than h³, which is to ensure mean-square convergence of 1.

Truncating the infinite series (A.1) and (A.2) to q terms, we have $I_{i j}^{q}$. From the truncated mean-square error in [21], we obtain the mean-square error for truncating (A.1)

$$ \begin{aligned} \mathrm{E}\left\{\left( I_{i j}\left( t_{n}, t_{n}+h\right)-I_{i j}^{q}\left( t_{n}, t_{n}+h\right)\right)^{2}\right\}\leq \frac{3 h^{2}}{2 \pi^{2} q}. \end{aligned} $$

Here we need 3h²/(2π²q) ≤ h³, so we should choose

$$ q_{t} \geq\left\lceil\frac{3}{2 \pi^{2} h}\right\rceil. $$

Truncating the expansion (A.1) to q, we get the mean-square error

$$ \begin{aligned} \mathrm{E}\left\{\left( I_{i j}\left( t_{n}, t_{n}+h\right)-I_{i j}^{q}\left( t_{n}, t_{n}+h\right)\right)^{2}\right\}\leq -\frac{h^{2}}{8} \ln \left|1-\frac{2}{2 q+1}\right|. \end{aligned} $$

Here we need the mean-square error less than h³, so we should choose

$$ q_{p} \geq\left\lceil\left( \frac{2}{1-e^{-8 h}}-1\right) / 2\right\rceil. $$

Since q_p ≈ 1/(8h), the truncated indices of A.1 and (A.2) both are O(1/h), and it can be calculated that the convergence speed of (A.1) is about q_t/q_p ≈ 1.22 times that of (A.2). This means that the approximation based on the multiple Legendre Fourier series is slightly more efficient than that based on the multiple trigonometric Fourier series.

1.2 A.2 Wiktorsson’s algorithm

If I(h) and A(h) are matrices with elements $I_{i j}\left (t_{n}, t_{n}+h\right )$, A_ii = 0 and

$$ A_{i j}(h)=\frac{h}{2\pi} {\sum}_{r=1}^{\infty} \frac{1}{r}\left\{\zeta_{2 r}^{(j)} \zeta_{2 r-1}^{(i)}-\zeta_{2 r-1}^{(j)} \zeta_{2 r}^{(i)}+\sqrt{2}\left( \zeta_{2 r-1}^{(j)} \zeta_{0}^{(i)}-\zeta_{0}^{(j)} \zeta_{2 r-1}^{(i)}\right)\right\},i\neq j $$

respectively, the approximation based on the multiple trigonometric Fourier series can be written in matrix form

$$ \begin{aligned} & \mathbf{I}(h)=\frac{{\varDelta} \mathbf{W}(h) {\varDelta} \mathbf{W}(h)^{\top}-h I_{m}}{2}+\mathbf{A}(h), \\ &\mathbf{A}(h)=\frac{h}{2 \pi} {\sum}_{k=1}^{\infty} \frac{1}{k}\left\{\mathbf{X}_{k}\left( \mathbf{Y}_{k}+\sqrt{2 / h} {\varDelta} \mathbf{W}(h)\right)^{\top}-\left( \mathbf{Y}_{k}+\sqrt{2 / h} {\varDelta} \mathbf{W}(h)\right) \mathbf{X}_{k}^{\top}\right\}, \end{aligned} $$

(A.3)

where ${\varDelta } \mathbf {W}(h) \sim N\left (0, h I_{m}\right ), \mathbf {X}_{k} \sim N\left (0_{m}, I_{m}\right )$ and $\mathbf {Y}_{k} \sim N\left (0_{m}, I_{m}\right ), k=$1, 2,…,q are all independent. As the Lévy stochastic area has the relationship I_ij − I_ji = 2A_ij, we only need to simulate I_ij for i < j or i > j in the simulation.

Wiktorsson’s algorithm is based on approximation of the tail-sum distribution of (A.3)

$$\varepsilon_{q}=\frac{h}{2 \pi} {\sum}_{k=q+1}^{\infty} \frac{1}{k}\left\{\mathbf{X}_{k}\left( \mathbf{Y}_{k}+\sqrt{2 / h} {\varDelta} \mathbf{W}(h)\right)^{\top}-\left( \mathbf{Y}_{k}+\sqrt{2 / h} {\varDelta} \mathbf{W}(h)\right) \mathbf{X}_{k}^{\top}\right\}, $$

which improves the rate of convergence. Let vec $\left (\mathbf {I}(h)^{T}\right )$ be column vectors of (A.3), and the following is the procedure of Wiktorsson’s algorithm [22]:

• 1. First simulate ${\varDelta } \mathbf {W}(h) \sim N\left (0_{m}, \sqrt {h} I_{m}\right )$.

• 2. Simulate the truncated first q terms

  $$ \tilde{A}^{(q)}(h)=\frac{h}{2 \pi} {\sum}_{k=1}^{q} \frac{1}{k} K_{m}\left( P_{m}-I_{m^{2}}\right)\left\{\left( \mathbf{Y}_{k}+\sqrt{\frac{2}{h}} {\varDelta} \mathbf{W}(h)\right) \otimes \mathbf{X}_{k}\right\} $$

  where $\mathbf {X}_{k} \sim N\left (0_{m}, I_{m}\right )$ and $\mathbf {Y}_{k} \sim N\left (0_{m}, I_{m}\right )$

• 3. Then simulate $\mathbf {G}_{q} \sim N\left (0_{M}, I_{M}\right )$ and add the approximation of tail-sum distribution:

  $$ \widetilde{A}^{(q)^{\prime}}(h)=\widetilde{A}^{(q)}(h)+\frac{h}{2 \pi} a_{q}^{1 / 2} \sqrt{{\Sigma}_{\infty}} \mathbf{G}_{q} $$

  where $a_{q}={\sum }_{k=q+1}^{\infty } 1 / k^{2}$

• 4. Finally obtain the approximation vec $\left (\mathbf {I}(h)^{T}\right )^{(q)^{\prime }}$ of vec $\left (\mathbf {I}(h)^{T}\right )$

  $$ \operatorname{vec}\left( \mathbf{I}(h)^{T}\right)^{(q)^{\prime}}=\frac{{\varDelta} \mathbf{W}(h) \otimes {\varDelta} \mathbf{W}(h)-\operatorname{vec}\left( h I_{m^{2}}\right)}{2}+\left( I_{m^{2}}-P_{m}\right) {K_{m}^{T}} \widetilde{A}^{(q)^{\prime}}(h) $$

  Here P_m is the m² × m² permutation matrix and for the specific expression of matrices P_m please refer to [22].

The mean-square error of Wiktorsson’s algorithm [22] is

$$ \underset{i, j}{\max} E\left\{\left( I_{i j}(h)-I_{i j}^{(q)^{\prime}}(h)\right)^{2}\right\} \leq \frac{5 h^{2}}{24 \pi^{2} q^{2}} m^{2}(m-1). $$

Here we also need the mean-square error less than h³, so we should choose truncated indices as

$$ q_{w} \geq\left\lceil\frac{\sqrt{5 m^{2}(m-1) /\left( 24 \pi^{2}\right)}}{\sqrt{ h}}\right\rceil, $$

and the truncated indices q_w is $O(1/\sqrt {h})$ that is much better than O(1/h).