Abstract
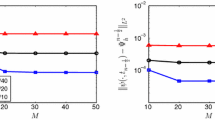
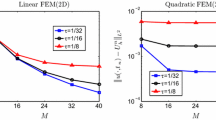
This paper presents a fully discrete scheme by discretizing the space with the Legendre-Galerkin method and the time with the Crank-Nicolson method to solve the two-dimensional second-order wave equation. Unconditional stability and optimal error estimates in both L2 and H1 norms of the fully discrete Crank-Nicolson Galerkin method are obtained. Numerical results confirm exponential convergence of the proposed method in space and second-order convergence in time. Also, the numerical experiments show the discrete energy conservation and efficiency of long-time numerical calculation.



Similar content being viewed by others
References
Bause, M., Köcher, U., Radu, F.A., Schieweck, F.: Post-processed Galerkin approximation of improved order for wave equations. Math. Comp. 89 (322), 595–627 (2020). https://doi.org/10.1090/mcom/3464
Bernardi, C., Maday, Y.: Spectral methods. In: Ciarlet, P.G., Lions, J.L. (eds.) Handbook of Numerical Analysis, pp 209–486. Elsevier, Amsterdam (1997)
Billingham, J., King, A.: Wave Motion. Cambridge University Press, Cambridge (2000)
Chou, C., Shu, C., Xing, Y.: Optimal energy conserving local discontinuous Galerkin methods for second-order wave equation in heterogeneous media. J. Comput. Phys. 272, 88–107 (2014)
Gao, H., Li, B., Sun, W.: Optimal error estimates of linearized Crank-Nicolson Galerkin FEMs for the time-dependent Ginzburg-Landau equations in superconductivity. SIAM J. Numer. Anal. 52(3), 1183–1202 (2014). https://doi.org/10.1137/130918678
Grote, M., Mehlin, M., Sauter, S.: Convergence analysis of energy conserving explicit local time-stepping methods for the wave equation. SIAM J. Numer. Anal. 56(2), 994–1021 (2018). https://doi.org/10.1137/17M1121925
Grote, M., Schneebeli, A., Schötzau, D.: Discontinuous Galerkin finite element method for the wave equation. SIAM J. Numer. Anal. 44(6), 2408–2431 (2006). https://doi.org/10.1137/05063194X
Grote, M., Schötzau, D.: Optimal error estimates for the fully discrete interior penalty DG method for the wave equation. J. Sci. Comput. 40(1-3), 257–272 (2009). https://doi.org/10.1007/s10915-008-9247-z
Hou, B., Liang, D.: Energy-preserving time high-order AVF compact finite difference schemes for nonlinear wave equations with variable coefficients. J. Comput. Phys. 421(109738), 27 (2020). https://doi.org/10.1016/j.jcp.2020.109738
Li, D., Wang, J.: Unconditionally optimal error analysis of Crank-Nicolson Galerkin FEMs for a strongly nonlinear parabolic system. J. Sci. Comput. 72 (2), 892–915 (2017). https://doi.org/10.1007/s10915-017-0381-3
Li, M., Shi, D., Wang, J.: Unconditional superconvergence analysis of a linearized Crank-Nicolson Galerkin FEM for generalized Ginzburg-Landau equation. Comput. Math. Appl. 79(8), 2411–2425 (2020). https://doi.org/10.1016/j.camwa.2019.11.008
Liu, W., Sun, J., Wu, B.: Space-time spectral method for the two-dimensional generalized sine-Gordon equation. J. Math. Anal. Appl. 427(2), 787–804 (2015)
Shan, Y., Liu, W., Wu, B.: Space–time Legendre–Gauss–Lobatto collocation method for two-dimensional generalized sine-Gordon equation. Appl. Numer. Math. 122, 92–107 (2017)
Shen, J.: Efficient spectral-Galerkin method I. Direct solvers for second- and fourth-order equations by using Legendre polynomials. SIAM J. Sci. Comput. 15(6), 1489–1505 (1994)
Shen, J., Tang, T., Wang, L.: Spectral Methods: Algorithms, Analysis and Applications. Springer-Verlag, New York (2011)
Shi, D., Wang, J.: Unconditional superconvergence analysis of a Crank-Nicolson Galerkin FEM for nonlinear Schrödinger equation. J. Sci. Comput. 72 (3), 1093–1118 (2017). https://doi.org/10.1007/s10915-017-0390-2
Shi, W., Wu, X., Xia, J.: Explicit multi-symplectic extended leap-frog methods for Hamiltonian wave equations. J. Comput. Phys. 231(22), 7671–7694 (2012). https://doi.org/10.1016/j.jcp.2012.07.004
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems, 2nd Ed. Springer-Verlag, Berlin (2006)
Wang, J.: Unconditional stability and convergence of Crank-Nicolson Galerkin FEMs for a nonlinear Schrödinger-Helmholtz system. Numer. Math. 139(2), 479–503 (2018). https://doi.org/10.1007/s00211-017-0944-0
Wu, X.: A note on stability of multidimensional adapted Runge-Kutta-Nyström methods for oscillatory systems. Appl. Math. Model. 36(12), 6331–6337 (2012). https://doi.org/10.1016/j.apm.2012.01.053
Acknowledgements
The authors are very grateful to the referees for careful reading of the paper and for their useful comments and suggestions which have improved the paper.
Funding
The research of the first author was supported by the National Natural Science Foundation of China (Nos. 11801120 and 11771107), the Fundamental Research Funds for the Central Universities (Grant No.HIT.NSRIF.2020081), the Natural Science Foundation of Heilongjiang Province (No. LH2020A004) and the Guangdong Basic and Applied Basic Research Foundation (No. 2020B1515310006). The research of the second author was supported by the National Natural Science Foundation of China (Nos. 11971131, U1637208, 61873071, 51476047).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix. Proof of Lemma 2.2
Appendix. Proof of Lemma 2.2
Derive the inequality: for \(v\in {V_{N}^{2}}\),
Recall that inverse inequality (cf. [15, P. 115]): for \(v\in P_{N}(\supseteq V_{N}),\)
Using the identities
we get
Together with (2.6), we obtain
Then, exploiting Poincaré inequality: for v ∈ VN,
Together with (2.6), we obtain
By Definition 2.1 with v → u, we have
By (A.1), we obtain
which implies (2.7) and \(\lambda _{\mathcal {A}}\in \mathbb {R}^{+}\). This completes the proof.
Rights and permissions
About this article
Cite this article
Liu, W., Wu, B. Unconditional stability and optimal error estimates of a Crank-Nicolson Legendre-Galerkin method for the two-dimensional second-order wave equation. Numer Algor 90, 137–158 (2022). https://doi.org/10.1007/s11075-021-01182-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-021-01182-x