Finite difference formulas in the complex plane

Abstract

Among general functions of two variables f(x, y), analytic functions f(z) with z = x + iy form a very important special case. One consequence of analyticity turns out to be that 2-D finite difference (FD) formulas can be made remarkably accurate already for small stencil sizes. This article discusses some key properties of such complex plane FD formulas. Application areas include numerical differentiation, interpolation, contour integration, and analytic continuation.

Appendices

Appendix 1: Code examples for the two weights algorithms

Let the task be to determine the weight set for the second derivative (i.e., L = d²/dz²) at the center of a 5 × 5 stencil. The next two sections illustrate how this can be done with the two methods described in Section 2. Comments indicate how to generalize to other node layouts and linear operators.

1.1 Method 1: MATLAB code

For node spacing h, we replace x = -2,2; by x = (-2,2)⋆h;. This code produces the same matrix as shown below for the Mathematica code, but as floating point numbers. Since the linear system is of Vandermonde type, it is prone to numerical ill-conditioning. In the present test case, using standard double precision, about 4 digits get lost, leading to coefficient errors up to about 10^− 12. Since the loss increases rapidly with stencil size, either exact rational or extended precision arithmetic is recommended (available in all common symbolic algebra packages). When using MATLAB, both are available through its symbolic toolbox; the latter also with the Advanpix toolbox¹⁴.

1.2 Method 2: Mathematica code

The following three Mathematica statements

compute the FD weights in closed form (with h as before denoting the node spacing). The further statement

displays this set of weights in a standard matrix format:

Appendix 2: Stencils of size 5 × 5 for the first four derivatives

$$ f^{\prime}(0)=\frac{1}{h}\left[\begin{array}{ccccc} \frac{1+i}{477360} & \frac{4(-1-i)}{29835} & \frac{i}{1326} & \frac{4(1-i)}{29835} & \frac{-1+i}{477360}\\ \frac{4(-1-i)}{29835} & \frac{8(-1-i)}{351} & \begin{array}{c} \\ \end{array}\frac{-8i}{39}\begin{array}{c} \\ \end{array} & \frac{8(1-i)}{351} & \frac{4(1-i)}{29835}\\ \frac{1}{1326} & \frac{-8}{39} & 0 & \frac{8}{39} & \frac{-1}{1326}\\ \frac{4(-1+i)}{29835} & \frac{8(-1+i)}{351} & \begin{array}{c} \\ \end{array}\frac{8i}{39}\begin{array}{c} \\ \end{array} & \frac{8(1+i)}{351} & \frac{4(1+i)}{29835}\\ \frac{1-i}{477360} & \frac{4(-1+i)}{29835} & \frac{-i}{1326} & \frac{4(1+i)}{29835} & \frac{-1-i}{477360} \end{array}\right]f+O(h^{24}), $$

$$ f^{\prime\prime}(0)=\frac{1}{h^{2}}\left[\begin{array}{ccccc} \frac{-i}{477360} & \frac{8(-1+3i)}{149175} & \frac{1}{1326} & \frac{8(-1-3i)}{149175} & \frac{i}{477360}\\ \frac{8(1+3i)}{149175} & \frac{16i}{351} & \begin{array}{c} \\ \end{array}\frac{-16}{39}\begin{array}{c} \\ \end{array} & \frac{-16i}{351} & \frac{8(1-3i)}{149175}\\ \frac{-1}{1326} & \frac{16}{39} & 0 & \frac{16}{39} & \frac{-1}{1326}\\ \frac{8(1-3i)}{149175} & \frac{-16i}{351} & \begin{array}{c} \\ \end{array}\frac{-16}{39}\begin{array}{c} \\ \end{array} & \frac{16i}{351} & \frac{8(1+3i)}{149175}\\ \frac{i}{477360} & \frac{8(-1-3i)}{149175} & \frac{1}{1326} & \frac{8(-1+3i)}{149175} & \frac{-i}{477360} \end{array}\right]f+O(h^{23}), $$

$$ f^{(3)}(0)=\frac{1}{h^{3}}\left[\begin{array}{ccccc} \frac{-1+i}{636480} & \frac{8(7-i)}{248625} & \frac{-i}{884} & \frac{8(-7-i)}{248625} & \frac{1+i}{636480}\\ \frac{8(1-7i)}{248625} & \frac{8(1-i)}{117} & \begin{array}{c} \\ \end{array}\frac{16i}{13}\begin{array}{c} \\ \end{array} & \frac{8(-1-i)}{117} & \frac{8(-1-7i)}{248625}\\ \frac{1}{884} & \frac{-16}{13} & 0 & \frac{16}{13} & \frac{-1}{884}\\ \frac{8(1+7i)}{248625} & \frac{8(1+i)}{117} & \begin{array}{c} \\ \end{array}\frac{-16i}{13}\begin{array}{c} \\ \end{array} & \frac{8(-1+i)}{117} & \frac{8(-1+7i)}{248625}\\ \frac{-1-i}{636480} & \frac{8(7+i)}{248625} & \frac{i}{884} & \frac{8(-7+i)}{248625} & \frac{1-i}{636480} \end{array}\right]f+O(h^{22}), $$

$$ f^{(4)}(0)=\frac{1}{h^{4}}\left[\begin{array}{ccccc} \frac{1}{318240} & \frac{32(-9-13i)}{1243125} & \frac{-1}{442} & \frac{32(-9+-13i)}{1243125} & \frac{1}{318240}\\ \frac{32(-9+-13i)}{1243125} & \frac{-32}{117} & \begin{array}{c} \\ \end{array}\frac{64}{13}\begin{array}{c} \\ \end{array} & \frac{-32}{117} & \frac{32(-9-13i)}{1243125}\\ \frac{-1}{442} & \frac{64}{13} & \frac{-92937}{5000} & \frac{64}{13} & \frac{-1}{442}\\ \frac{32(-9-13i)}{1243125} & \frac{-32}{117} & \begin{array}{c} \\ \end{array}\frac{64}{13}\begin{array}{c} \\ \end{array} & \frac{-32}{117} & \frac{32(-9+-13i)}{1243125}\\ \frac{1}{318240} & \frac{32(-9+-13i)}{1243125} & \frac{-1}{442} & \frac{32(-9-13i)}{1243125} & \frac{1}{318240} \end{array}\right]f+O(h^{21}). $$

For this stencil size, one can approximate up through f⁽²⁴⁾(0) which then becomes first-order accurate.

Appendix 3

Following up on Section 8, we consider again

$$ \phi(z)=\prod\limits_{\eta=1}^{N}(z-z_{\eta})=\prod\limits_{\begin{array}{c} \mu=-n,\ldots,+n\\ \nu=-n,\ldots,+n \end{array}}(z-(\mu+i \nu)), $$

and note that

$$ \phi^{\prime}(z_{k})=\prod\limits_{\begin{array}{c} \eta=1\\ \eta\neq k \end{array}}^{N}(z_{k}-z_{\eta}). $$

(24)

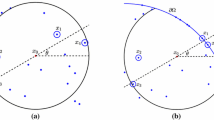
We next refer to Fig. 8, with a schematic illustration in the n = 4 case (with a total of N = (2n +-1)² = 81 nodes), and μ = 2, ν = 1, i.e., z_k = 2 + i (marked by a triangle, in contrast to z = 0 marked by a square). The value for $\phi ^{\prime }(0)$, according to (24), is obtained by a product over all nodes inside the large solid square (omitting its center node). If the corresponding product for $\phi ^{\prime }(z_{k})$ had used the nodes inside the dashed square (again omitting the center node), it would have evaluated to the same result. However, it does not, but a calculation for $\log |\phi ^{\prime }(0)|$ becomes a calculation for $\log |\phi ^{\prime }(z_{k})|$ if we to it add the sums

$$ S_{1}=\sum\limits_{z_{\eta}\textrm{ in rectangle }1}\log|z_{\eta}|,\qquad S_{2}=\sum\limits_{z_{\eta}\textrm{ in rectangle }2}\log|z_{\eta}| $$

and subtract

$$ S_{3}=\sum\limits_{z_{\eta}\textrm{ in rectangle }3}\log|z_{\eta}|,\qquad S_{4}=\sum\limits_{z_{\eta}\textrm{ in rectangle }4}\log|z_{\eta}|. $$

Each of these four sums is readily estimated to leading order. Along the center line of each of the four narrow rectangles (marked 1, 2, 3, 4 in the figure), we can approximate the sum by suitable use of the integral relation

$$ \begin{array}{@{}rcl@{}} {{\int}_{a}^{b}}\log(x^{2}+y^{2})dx&=&2y\left( \arctan\frac{b}{y}-\arctan\frac{a}{y}\right)+b\left( \log(b^{2}+y^{2})-2\right)\\&&-a\left( \log(a^{2}+y^{2})-2\right) \end{array} $$

Fig. 8

Illustration of the node sets used in the estimate of the sums S₁,…, S₄, as described in Appendix 10

together with multiplying each integral by the width (orthogonal to the center line) of the respective rectangle. After straightforward algebra, this gives

$$ S_{1}+S_{2}-S_{3}-S_{4}=\frac{\pi}{2}(\mu^{2}+\nu^{2})-\frac{1}{2n}(\mu^{2}+\nu^{2})+O\left( \frac{1}{n^{2}}\right), $$

(25)

from with (20) then follows.