Skip to main content
SpringerLink
Log in

Discrete mollification in Bernstein basis and space marching scheme for numerical solution of an inverse two-phase one-dimensional Stefan problem

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

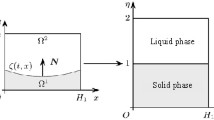
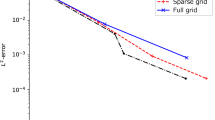
In this paper, a one-dimensional two-phase inverse Stefan problem is studied. The free surface is considered unknown here, which is more realistic from the practical point of view. The problem is ill-posed since small errors in the input data can lead to large deviations from the desired solution. To obtain a stable numerical solution, we propose a method based on discrete mollification combined with space marching. We use the integration matrix in Bernstein polynomial basis for the discrete mollification method. Through this method, our numerical integration does not involve any direct function integration and only contains algebraic calculations. Furthermore, the stability and convergence of the process are proved. Finally, the results of this paper are illustrated and examined through some numerical examples. The numerical examples supporting our theoretical analysis are provided and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Bodaghi, S., Zakeri, A., Amiraslani, A.: A numerical scheme based on discrete mollification method using Bernstein basis polynomials for solving the inverse onedimensional Stefan problem Inverse Problems in Science and Engineering. https://doi.org/10.1080/17415977.2020.1733996 (2020)

  2. Sazhin, S.S., Krutitskii, P.A., Gusev, I.G., Heikal, M.R.: Transient heating of an evaporating droplet. Int. J. Heat Mass Transfer 53, 2826–2836 (2010)

    Article  Google Scholar 

  3. Back, J.M., McCue, S.W., Hsieh, M.H.-N., Moroney, T.J.: The effect of surface tension and kinetic undercooling on a radially-symmetric melting problem. Appl. Math. Comput. 229, 41–52 (2014)

    MathSciNet  MATH  Google Scholar 

  4. Herrero, M.A., Velazquez, J.J.L.: On the melting of ice balls. SIAM J. Math. Anal. 28, 1–32 (1997)

    Article  MathSciNet  Google Scholar 

  5. McCue, S.W., Wu, B., Hill, J.M.: Classical two-phase Stefan problem for spheres. Proc. R. Soc. A 464, 2055–2076 (2008)

    Article  MathSciNet  Google Scholar 

  6. McCue, S.W., Hsieh, M., Moroney, T.J., Nelson, M.I.: Asymptotic and numerical results for a model of solvent-dependent drug diffusion through polymeric spheres. SIAM J. Appl. Math. 71, 2287–2311 (2011)

    Article  MathSciNet  Google Scholar 

  7. Pedroso, R.I., Domoto, G.A.: Perturbation solutions for spherical solidification of saturated liquids. J. Heat Transfer 95, 42–46 (1973)

    Article  Google Scholar 

  8. Riley, D.S., Smith, F.T., Poots, G.: The inward solidification of spheres and circular cylinders. Int. J. Heat Mass Transfer 17, 1507–1516 (1974)

    Article  Google Scholar 

  9. Soward, A.M.: A unified approach to Stefan’s problem for spheres. Proc. R. Soc. A 373, 131–147 (1980)

    MathSciNet  Google Scholar 

  10. Stewartson, K., Waechter, R.T.: On Stefan’s problem for spheres. Proc. R. Soc. A 348, 415–426 (1976)

    MathSciNet  Google Scholar 

  11. Tabakova, S., Feuillebois, F., Radev, S.: Freezing of a supercooled spherical droplet with mixed boundary conditions. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 466, 1117–1134 (2010)

    MATH  Google Scholar 

  12. Vynnycky, M.: On the onset of air-gap formation in vertical continuous casting with superheat. Int. J. Mech. Sci. 73, 69–76 (2013)

    Article  Google Scholar 

  13. Vynnycky, M.: A mathematical model for air-gap formation in vertical continuous casting: the effect of superheat. Trans. Indian Inst. Met. 62, 495–498 (2009)

    Article  Google Scholar 

  14. Acosta, C.D., Mejia, C.E.: Stabilization of explicit methods for convection diffusion equations by discrete mollification. Comput. Math. Appl. 55, 368–380 (2008)

    Article  MathSciNet  Google Scholar 

  15. Bakal, A., Timbers, G., Hayakawa, K.: Solution of the characteristic equation involved in the transient heat conduction for foods approximated by an infinite slab, Can Inst. Food Techtlol. 76 (1970)

  16. Bollati, J., Semitiel, J., Tarzia, D.A.: Heat balance integral methods applied to the one-phase Stefan problem with a convective boundary condition at the fixed face. Appl. Math. Comput. 331, 1–19 (2018)

    Article  MathSciNet  Google Scholar 

  17. Coles, C., Murio, D.A.: Identification of parameters in the 2-D IHCP. Comput. Math. Appl. 40, 939–956 (2000)

    Article  MathSciNet  Google Scholar 

  18. Conti, M.: Density change effects on crystal growth from the melt. Phys. Rev. E 64, 051601 (2001)

    Article  Google Scholar 

  19. Crank, J.: Free and Moving Boundary Problems. Clarendon Press, Oxford (1984)

    MATH  Google Scholar 

  20. Goldman, N.L.: Inverse Stefan Problem. Kluwer, Dordrecht (1997)

    Book  Google Scholar 

  21. Gupta, S.C.: The Classical Stefan Problem. Basic Concepts, Modelling and Analysis. Elsevier, Amsterdam (2003)

    MATH  Google Scholar 

  22. Johansson, T., Lesnic, D., Reeve, T.: A meshless method for an inverse two-phase one dimensional nonlinear Stefan problem. Math. Comput. Simul. 101, 61–77 (2014)

    Article  MathSciNet  Google Scholar 

  23. Libbrecht, K.G.: The physics of snow crystals. Rep. Prog. Phys. 68, 855 (2005)

    Article  Google Scholar 

  24. Lin, W.S.: Steady ablation on the surface of a two-layer composite, vol. 48. A. M. Meirmanov, The Stefan Problem, Walter de Gruyter, Berlin, 1992 (2005)

  25. Mejia, C.E., Murio, D.A.: Mollified hyperbolic method for coefficient identification problems. Comput. Math. Appl. 26(5), 1–12 (1993)

    Article  MathSciNet  Google Scholar 

  26. Mejia, C.E., Acosta, C.D., Saleme, K.I.: Numerical identification of a nonlinear diffusion coefficient by discrete mollification. Comput. Math. Appl. 62, 2187–2199 (2011)

    Article  MathSciNet  Google Scholar 

  27. Mejia, C.E., Murio, D.A.: Numerical solution of generalized IHCP by discrete mollification. Comput. Math. Appl. 32(2), 33–50 (1996)

    Article  MathSciNet  Google Scholar 

  28. Mitchell, S.L., Vynnycky, M.: Finite-difference methods with increased accuracy and correct initialization for one-dimensional Stefan problems. Appl. Math. Comput. 215, 1609–1621 (2009)

    MathSciNet  MATH  Google Scholar 

  29. Murio, D.A.: Mollification and space marching. In: Woodbury, K (ed.) Inverse Engineering Handbook, CRC Press (2002)

  30. Namenanee, K., McKenzie, J., Kosa, E., Schwab, M., Sunsaneewitayakul, B., Vasavakul, T., Khunnawat, C., Ngarmukos, T.: A new approach for catheter ablation of atrial fibrillation: mapping of the electrophysiologic substrate. J. Amer. College Cardiology 43(11), 2044–2053 (2004)

    Article  Google Scholar 

  31. Salva, N.N., Tarzia, D.A.: Explicit solution for a Stefan problem with variable latent heat and constant heat flux boundary conditions. J. Math. Anal. Appl. 379, 240–244 (2011)

    Article  MathSciNet  Google Scholar 

  32. Sharifi, N., Bergman, T.L., Allen, M.J., Faghri, A.: Melting and solidification enhancement using a combined heat pipe, foil approach. Int. J. Heat. Mass. Tran. 78, 930–941 (2015)

    Article  Google Scholar 

  33. Slota, D.: Direct and inverse one-phase Stefan problem solved by the variational iteration method. Comput. Math. Appl. 54, 113–1146 (2007)

    Article  MathSciNet  Google Scholar 

  34. Slota, D.: Homotopy perturbation method for solving the two-phase inverse Stefan problem. Numer. Heat Transfer PartA 59, 755–68 (2011)

    Article  Google Scholar 

  35. Rubinstein, L.I.: The Stefan Problem. AMS, Providence (1971)

    Google Scholar 

  36. Tayler, A.B.: Mathematical Models in Applied Mechanics. Oxford University Press, Oxford (2001)

    MATH  Google Scholar 

  37. Trueba, J.L., Voller, V.R.: Analytical and numerical solution of a generalized Stefan problem exhibiting two moving boundaries with application to ocean delta formation. J. Math. Anal. Appl. 366, 538–549 (2010)

    Article  MathSciNet  Google Scholar 

  38. Wrobel, L.C.: A Boundary Element Solution to Stefan’s Problem. In: Brebbia, C.A., Futagami, T., Tanaka, M. (eds.) Boundary Elements V, Computational Mechanics Publications, pp 173–182. Springer, Berlin (1983)

  39. El Badia, A., Moutazaim, F.: A one-phase inverse Stefan problem. Inverse Prob. 15, 1507–1522 (1999)

    Article  MathSciNet  Google Scholar 

  40. Cannon, J.R., Douglas, J.: The Cauchy problem for the heat equation. SIAM J. Numer. Anal. 4(3), 317–336 (1967)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematics, K. N. Toosi University of Technology, Tehran, Iran

    S. Bodaghi & A. Zakeri

  2. School of STEM, Department of Mathematics, Capilano University, 2055 Purcell Way, North Vancouver, BC, V7G 3J5, Canada

    A. Amiraslani

  3. Department of Mathematics, Faculty of Basic Science, Khatam-ol-Anbia (PBU) University, Tehran, Iran

    A. H. Salehi Shayegan

Authors
  1. S. Bodaghi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Zakeri
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Amiraslani
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. H. Salehi Shayegan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Zakeri.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bodaghi, S., Zakeri, A., Amiraslani, A. et al. Discrete mollification in Bernstein basis and space marching scheme for numerical solution of an inverse two-phase one-dimensional Stefan problem. Numer Algor 90, 1569–1592 (2022). https://doi.org/10.1007/s11075-021-01242-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-021-01242-2

Keywords

Search

Navigation