Abstract
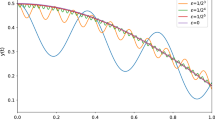
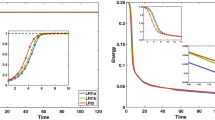
This paper is devoted to the construction and analysis of uniformly accurate (UA) nested Picard iterative integrators (NPI) for highly oscillatory second-order differential equations. The equations involve a dimensionless parameter ε ∈ (0,1], and their solutions are highly oscillatory in time with wavelength at \(\boldsymbol {\mathcal {O}}(\varepsilon ^{2})\), which brings severe burdens in numerical computation when ε ≪ 1. In this work, we first propose two NPI schemes for solving a differential equation. The schemes are uniformly first- and second-order accurate for all ε ∈ (0,1]. Moreover, they are super convergent when the time-step size is smaller than ε2. Then, the schemes are generalized to a system of differential equations with the same uniform accuracies. Error bounds are rigorously established and numerical results are reported to confirm the error estimates.



Similar content being viewed by others
Availability of data and material
The datasets generated during and/or analyzed during the current study are available from the author on reasonable request.
References
Ariel, G., Engquist, B, Tsai, R.: A multiscale method for highly oscillatory ordinary differential equations with resonance. Math. Comput. 78, 929–956 (2009)
Bao, W., Dong, X.: Analysis and comparison of numerical methods for the Klein-Gordon equation in the nonrelativistic limit regime. Numer. Math. 120, 189–229 (2012)
Bao, W., Zhao, X.: Comparison of numerical methods for the nonlinear Klein-Gordon equation in the nonrelativistic limit regime. J. Comput. Phys. 398, 108886 (2019)
Bao, W., Cai, Y., Zhao, X.: A uniformly accurate multiscale time integrator pseudospectral method for the Klein-Gordon equation in the nonrelativistic limit regime. SIAM J. Numer. Anal. 52, 2488–2511 (2014)
Bao, W., Dong, X., Zhao, X.: Uniformly accurate multiscale time integrators for highly oscillatory second order differential equations. J. Math. Study 47, 111–150 (2014)
Baumstark, S., Faou, E., Schratz, K.: Uniformly accurate exponential-type integrators for Klein-Gordon equations with asymptotic convergence to the classical NLS splitting. Math. Comp. 87, 1227–1254 (2018)
Cai, Y., Wang, Y.: Uniformly accurate nested Picard iterative integrators for the Dirac equation in the nonrelativistic limit regime. SIAM J. Numer. Anal. 57, 1602–1624 (2019)
Castella, F., Chartier, P., Méhats, F., Murua, A.: Stroboscopic averaging for the nonlinear schrödinger equation. Found. Comput. Math. 15, 519–559 (2015)
Chartier, P., Crouseilles, N., Lemou, M., Méhats, F.: Uniformly accurate numerical schemes for highly oscillatory Klein-Gordon and nonlinear schrödinger equations. Numer. Math. 129, 211–250 (2015)
Cohen, D.: Conservation properties of numerical integrators for highly oscillatory Hamiltonian systems. IMA J. Numer. Anal. 26, 34–59 (2005)
Cohen, D., Hairer, E., Lubich, C.: Modulated Fourier expansions of highly oscillatory differential equations. Found. Comput. Math. 3, 327–345 (2003)
Cohen, D., Hairer, E., Lubich, C.: Numerical energy conservation for multi-frequency oscillatory differential equations. BIT Numer. Math. 45, 287–305 (2005)
Cohen, D., Hairer, E., Lubich, C.: Conservation of energy, momentum and actions in numerical discretizations of non-linear wave equations. Numer. Math. 110, 113–143 (2008)
Condon, M., Deaño, A., Iserles, A: On highly oscillatory problems arising in electronic engineering. ESAIM Math. Model. Numer. Anal. 43, 785–804 (2009)
Condon, M., Deaño, A., Iserles, A: On second order differential equations with highly oscillatory forcing terms. Proc. R. Soc. A 466, 1809–1828 (2010)
Duncan, D. B.: Symplectic finite difference approximations of the nonlinear Klein-Gordon equation. SIAM J. Numer. Anal. 34, 1742–1760 (1997)
Engquist, B., Tsai, Y.: Heterogeneous multiscale methods for stiff ordinary differential equations. Math. Comp. 74, 1707–1742 (2005)
Faou, E., Schratz, K.: Asymptotic preserving schemes for the Klein-Gordon equation in the non-relativistic limit regime. Numer. Math. 126, 441–469 (2014)
Garcia-Archilla, B., Sanz-Serna, J.M., Skeel, R.D.: Long-time-step methods for oscillatory differential equations. SIAM J. Sci. Comput. 20, 930–963 (1998)
Gauckler, L.: Error analysis of trigonometric integrators for semilinear wave equations. SIAM J. Numer. Anal. 53, 1082–1106 (2015)
Gautschi, W.: Numerical integration of ordinary differential equations based on trigonometric polynomials. Numer. Math. 3, 381–397 (1961)
Grimm, V., Hochbruck, M.: Error analysis of exponential integrators for oscillatory second-order differential equations. J. Phys. A: Math. Gen. 39, 5495–5507 (2006)
Hairer, E., Lubich, C.: Long-time energy conservation of numerical methods for oscillatory differential equations. SIAM J. Numer. Anal. 38, 414–441 (2000)
Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations. Springer, Berlin (2006)
Hochbruck, M., Ostermann, A.: A Gautschi-type method for oscillatory second-order differential equations. Numer. Math. 83, 403–426 (1999)
Hochbruck, M., Ostermann, A.: Exponential integrators. Acta Numer. 19, 209–286 (2010)
Iserles, A: On the numerical quadrature of highly-oscillating integrals I: Fourier transforms. IMA J. Numer. Anal. 24, 365–391 (2004)
Lorenz, K., Jahnke, T., Lubich, C.: Adiabatic integrators for highly oscillatory second-order linear differential equations with time-varying eigendecomposition. BIT Numer. Math. 45, 91–115 (2005)
Machihara, S., Nakanishi, K., Ozawa, T.: Nonrelativistic limit in the energy space for nonlinear Klein-Gordon equations. Math. Ann. 322, 603–621 (2002)
Masmoudi, N., Nakanishi, K.: From nonlinear Klein-Gordon equation to a system of coupled nonlinear Schrödinger equations. Math. Ann. 324, 359–389 (2002)
Najman, B: The nonrelativistic limit of the nonlinear Klein-Gordon equation. Nonlinear Anal. 15, 217–228 (1990)
Ostermann, A., Schratz, K.: Low regularity exponential-type integrators for semilinear Schrödinger equations. Found. Comput. Math. 18, 731–755 (2018)
Sanz-Serna, J. M.: Mollified impulse methods for highly oscillatory differential equations. SIAM J. Numer. Anal. 46, 1040–1059 (2008)
Sanz-Serna, J. M.: Modulated Fourier expansions and heterogeneous multiscale methods. IMA J. Numer. Anal. 29, 595–605 (2009)
Schratz, K., Wang, Y., Zhao, X.: Low-regularity integrators for nonlinear Dirac equations. Math. Comp. 90, 189–214 (2021)
Strauss, W., Vázquez, L.: Numerical solution of a nonlinear Klein-Gordon equation. J. Comput. Phys. 28, 271–278 (1978)
Tao, T.: Local and Global Analysis of Nonlinear Dispersive and Wave Equations. CBMS Regi. Cmf. Ser. Math. AMS, Providence (2006)
Tsutsumi, M.: Nonrelativistic approximation of nonlinear Klein-Gordon equations in two space dimensions. Nonlinear Anal. 8, 637–643 (1984)
Wang, B., Iserles, A., Wu, X.: Arbitrary-order trigonometric Fourier collocation methods for multi-frequency oscillatory systems. Found. Comput. Math. 16, 151–181 (2016)
Weinan, E.: Analysis of the heterogeneous multiscale method for ordinary differential equations. Commun. Math. Sci. 1, 423–436 (2003)
Weinan, E., Engquist, B., Li, X., Ren, W., Vanden-Eijnden, E.: The heterogeneous multiscale method: a review. Commun. Comput. Phys. 2, 367–450 (2007)
Zhao, X.: Uniformly accurate (UA) multiscale time integrators for second order oscillatory differential equations with large initial data. BIT Numer. Math. 57, 649–683 (2017)
Funding
This work was partially supported by the National Natural Science Foundation of China grants 12001221, Hubei Provincial Science and Technology Innovation Base (Platform) Special Project 2020DFH002, and the Fundamental Research Funds for the Central Universities CCNU19TD010.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Define
The functions used in the first-order NPI scheme (11) with (8) are:
For the second-order NPI scheme, we further define
The functions used in the second-order NPI scheme (12) with (10) are:
for k = 1, 3, 5 with
for j = 1, 2.
Appendix 2
Define
The functions used in the modified first-order NPI scheme (19)–(21) are:
When considering the nonlinearity f(z) = diag(zz∗)z, we only need to change the above an,bn,cn to the following expressions:
Appendix 3
Proof Proof of Theorem 2
Noticing that \(\lvert {\sin \limits } x\rvert \le \lvert x\rvert \), we could modify the estimates (34), (35), (41), and (42), respectively, as
Thus, the error estimate for the error energy becomes
which leads to the error bound \(\lvert y(t_{n}) - y^{n}\rvert + \varepsilon ^{2} \lvert \dot {y}(t_{n}) - \dot {y}^{n}\rvert \le C \frac {\tau ^{4}}{\varepsilon ^{4}}\). □
Appendix 4
Rights and permissions
About this article
Cite this article
Wang, Y. On nested Picard iterative integrators for highly oscillatory second-order differential equations. Numer Algor 91, 1627–1651 (2022). https://doi.org/10.1007/s11075-022-01317-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-022-01317-8